基于量纲分析的简单线性轮廓与多变量的测量系统能力评价

刘小娜，曹 瑜，韩正超，张 怡



基于量纲分析的简单线性轮廓与多变量的测量系统能力评价

刘小娜，曹 瑜，韩正超，张 怡

（昆明理工大学 机电工程学院，云南 昆明 650504）

测量系统分析是统计质量改进或控制的一项主要内容，目前，多元测量系统的分析和评价运用多元方差分析法或主成分分析法较多，在实际生产过程中，存在简单线性轮廓与多变量质量特性的复杂多元测量系统的情况，而针对这种复杂多元测量系统能力评估的研究较少。本文提出了基于量纲分析的复杂多元测量系统能力评价方法，集成物理和统计分析，利用物理中量纲分析的方法研究产品或过程各相关变量之间的物理关系，将多元转化为一元测量系统问题，再利用一元测量系统能力评估的统计方法及指标来对测量系统能力进行评价。最后，本文再现经典纸飞机试验，运用所提量纲分析方法对纸飞机的测量系统进行分析和评价，验证方法的有效性。

测量系统分析；测量系统能力评价；简单线性轮廓；量纲分析

0 引言

测量在生产制造过程中对于产品或零件的加工是必不可少的过程和步骤，而数据就是测量的结果。测量系统是由人员、量具、测量方法和测量对象等组成的过程整体，在这个整体集合中进行过程的输入与输出。许多过程输出的问题就是测量系统造成的，因此建立准确有效的测量系统是质量改进与控制的第一步。所谓测量系统分析，是指用统计学的方法来了解测量系统中的各个波动源以及它们对测量结果的影响，来分析判断整个测量系统是否合乎要求[1]。

Eagle[2]和Grubbs[3]最早开始从统计角度进行测量系统的误差研究。Mandal[4]于1972年首次引入测量系统的重复性与再现性概念，并同时提出了两个测量系统能力评价指数即精度公差比（P/T%）和重复性与再现性百分比（R&R%）。除了这两个测量系统评价指数提出后被广泛运用外，两个新的测量系统评价指数分辨率（DR）和信噪比（SNR）分别被Mander[5]于1999年和AIAG[6]于2010年引入后广泛引用。这几个能力评价指标在单变量质量特性中经常被当作是质量改进评价标准的评判。

通常情况下，通过测量一种产品或过程的质量特征指标来达到对产品质量评估的目的，但是面对现代制造产品，往往需要对一种产品多种特性进行测量。在对多元测量系统进行能力评价中，Wang和Chern[7]利用自助法对设计容差为圆形的二元测量系统中的圆形直径建立置信区间，通过仿真研究验证方法的有效性。Majeske[8]利用MANOVA模型估算出方差-协方差矩阵从而得出多元评价指数的估计值以评价多元测量系统。但是这种方法更多的是建立在统计理论上，由于被测的质量特性之间存在相关性，不能简单地将多元测量系统分为多个一元测量系统进行评价。如果考虑被测质量特性之间的物理特性，就可以利用这种物理关系来降低测量产品质量的复杂程度和工作量。

而本文的简单线性轮廓与多变量质量特性的多元测量系统是一种更为复杂的多元测量系统，目前进行这种测量系统的分析和研究较少。针对这种复杂测量系统，本文提出一种集成量纲分析（dimensional analysis, DA）的方法进行测量系统的能力评估。通过分析简单线性轮廓与多变量之间的物理函数关系，应用量纲理论，求出各变量之间的物理关系达到降维目的，使得多元变为一元问题，再利用一元的评价方法进行评估，从而使得对复杂测量系统的评价更简单有效。本文主要分为4个部分。首先引入对测量系统分析及其能力评估的研究，接着对前人所提出的测量系统分析的方法及指标进行研究，然后讨论量纲分析方法应用到轮廓与多变量测量系统进行能力评价，最后通过一个案例验证集成量纲分析方法进行测量系统能力评估的有效性和实用性。

1 简单线性轮廓与多变量质量特性的测量系统能力评价

1.1 测量系统分析

目前，均值极差法和方差分析法（ANOVA）是两种评价测量系统重复性和再现性的方法，其区别在于是否考虑零件间与操作者的交互作用；前者不考虑交互作用，后者优先考虑交互作用是否存在，所以它的精确性更高，适合实验分析。通过方差分析，得到测量系统不同效应的方差分量，再利用这些方差分量建立评价指标。对测量系统能力的评价，一般使用评价指数精度公差比（P/T%）、重复性与再现性百分比（R&R%）和信噪比（SNR）等，其中P/T%和R&R%的公式如（1）和（2）所示：

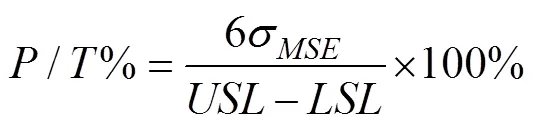
表1 对评价指标（P/T%）和（R&R%）评判标准

Tab.1 Criteria for evaluation indicators (P/T%) and (R&R%)

标准的测量系统评价指标针对的是单一质量特性的测量系统进行分析评价，但在实际的生产制造过程中需要对多个质量特性进行测量。目前对多元测量系统的能力评价使用较多的方法是基于多元方差分析方法。Majeske认为当测量系统的评价指标由一元拓展到多元时，多元P/T%和R&R%比率是两个体积大小的比值。在多元统计中，多元正态分布的连续密度函数曲线是以均值为中心的多维椭球体。而该方法的不足之处是当多维椭球体的分布和公差发生变化时，指标无法识别，而且，该方法没有考虑被测特性间是否存在物理关系。

1.2 量纲分析

量纲分析法（DA）又称为因次分析法，是一种数学分析方法，也是研究物理问题的重要方法之一，它根据一切量所必须具有的形式来分析判断事物间数量关系所遵循的一般规律。在国际单位制中，有7个基本量纲：长度、质量、时间、电流、热力学温度、物质的量、发光强度，其他的量纲均可由基本量纲导出。

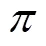
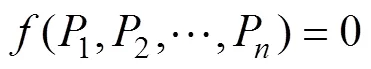
然后再转化成无量纲变量：

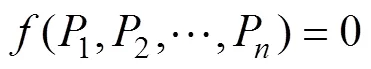
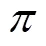
1.3 简单线性轮廓与多变量质量特性的测量系统

复杂产品的多变量质量特性之间有时存在某种函数关系，这种函数关系称为轮廓（profile）[10]，轮廓通常描述为一种响应变量和一种或多种解释变量之间的关系，而最常见的轮廓关系是简单线性轮廓。目前对轮廓的研究可以应用到许多领域，例如产品的制造、检验、校准等工业过程。在制造和服务业，常用轮廓这一概念来评价制造过程或服务过程随着时间或空间性能好坏的变化。

简单线性轮廓和多元变量的组合构成了具有相关关系的线性轮廓与多变量质量特性的多元复杂测量系统，而这种测量系统就是用来描述和测量复杂产品或过程的质量特性并对其进行测量系统能力评价。Ebadi和Shahriari[11]分别基于响应变量的实际观测值和预测值提出两种方法对简单线性轮廓的测量系统的过程能力进行计算和分析。Ghartemani等[12]提出由三个元素组成的多元过程能力指数向量实现对简单线性轮廓的测量系统进行能力评价。吴小芳[13]通过构建二维预测轮廓向量来评价轮廓测量系统的过程能力，当然，还有许多国内外学者也做了大量的有关研究。

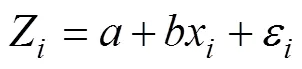
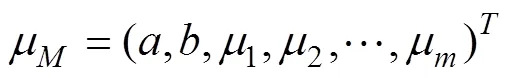
通过构建多维统计向量，把具有相关关系的简单线性轮廓与多元质量特性的测量系统利用轮廓参数与多元影响因子转化为一个多维向量，这样转化可降低本文所要研究测量系统的难度，再利用集成 量纲方法来对测量系统进行能力评价。

1.4 集成DA简单线性轮廓与多变量质量特性的测量系统能力评价的方法

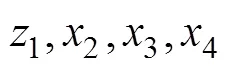
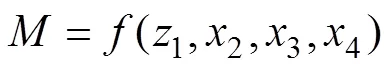
表2 量纲矩阵

Tab.2 Dimensional matrix

所以求得无量纲变量分别是

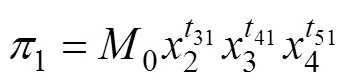
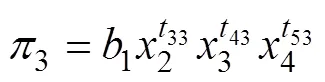
无量纲变量之间的关系式可表示为

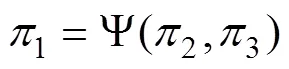
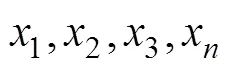
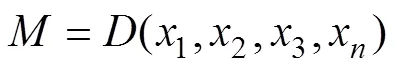
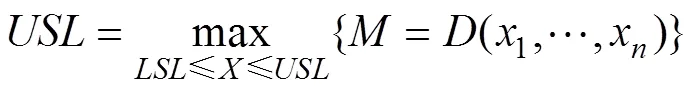
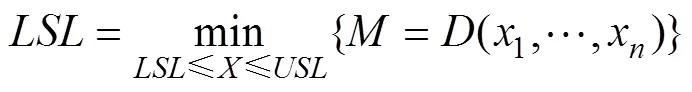
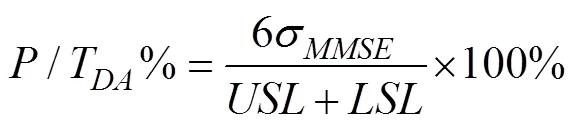
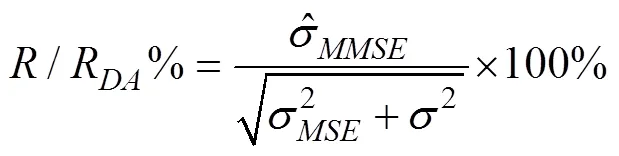
2 案例分析

表3 直接测量数据

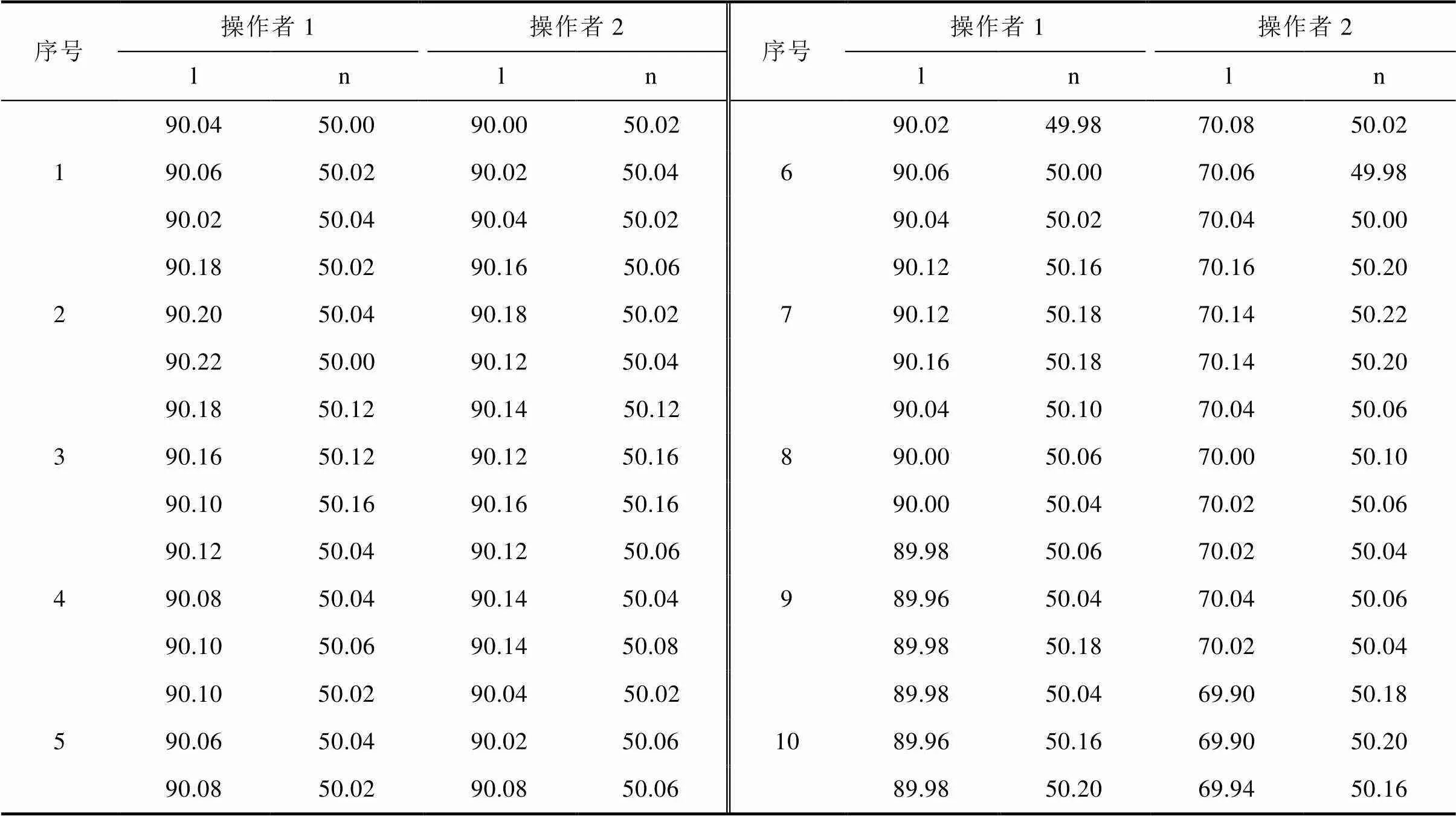
Tab.3 Direct measurement data

根据公式推导，已知纸飞机产品的相关物理变量，纸飞机的飞行时间和纸飞机各项参数满足关系式：

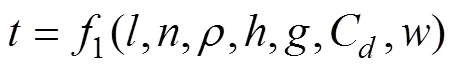
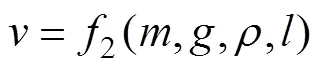
将此关系式用量纲矩阵表示成表4。

表4 量纲矩阵

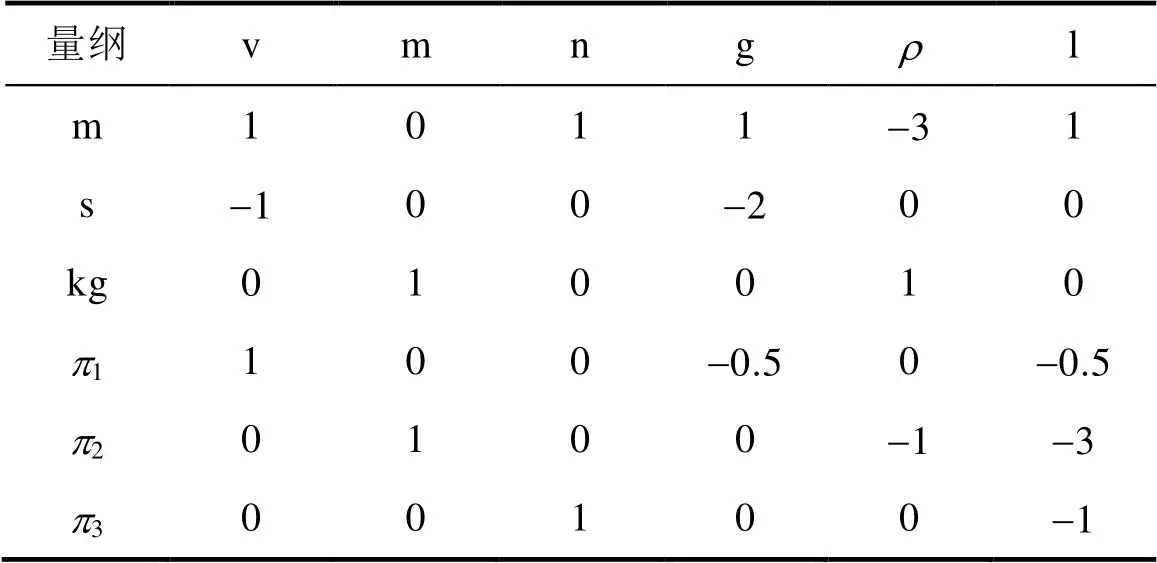
Tab.4 Dimensional matrix

由上表可知系统中的无量纲为

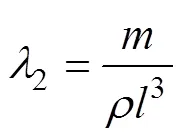
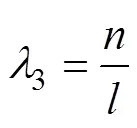
假设这3个无量纲变量之间的关系式是

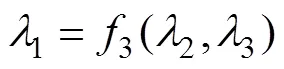
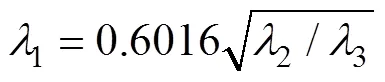
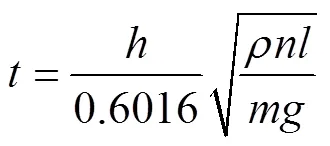
根据式（26）可将表4的数据转化为纸飞机的飞行时间，得到表5。

利用方差分析对数据进行处理，得到双因子方差分析如表6。

再由表6结果利用量纲分析得到表7和表8的测量系统能力评价指标的值。

由以上表可看出，该测量系统的R&RDA%是14.63%，P/TDA%是29.51%，两个指标均介于10%和30%之间，所以该测量系统的能力有待提高。

表5 处理后的数据

Tab.5 Data processed

表6 包含交互作用的双因子方差分析表

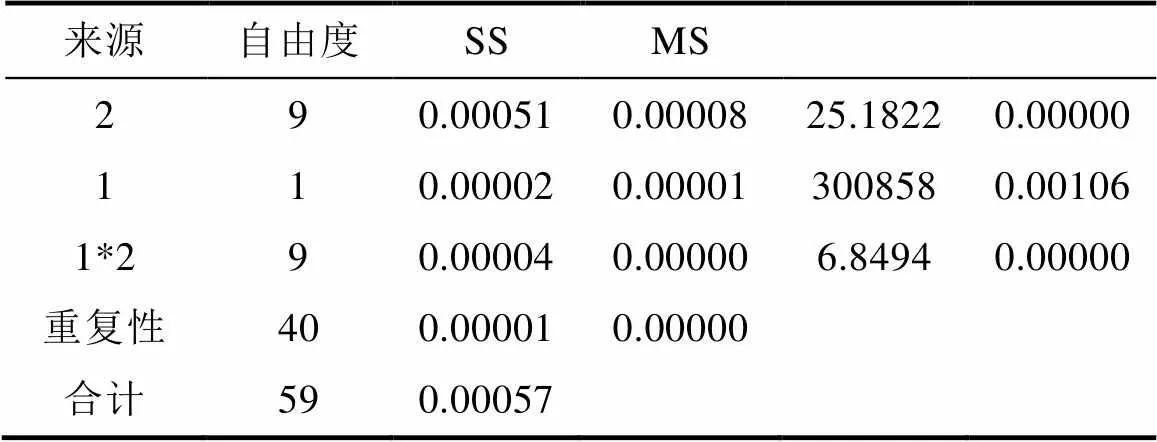
Tab.6 Double factor ANOVA with interaction

表7 量具R&R%

Tab.7 Gauge R&R%

表8 变异公差比

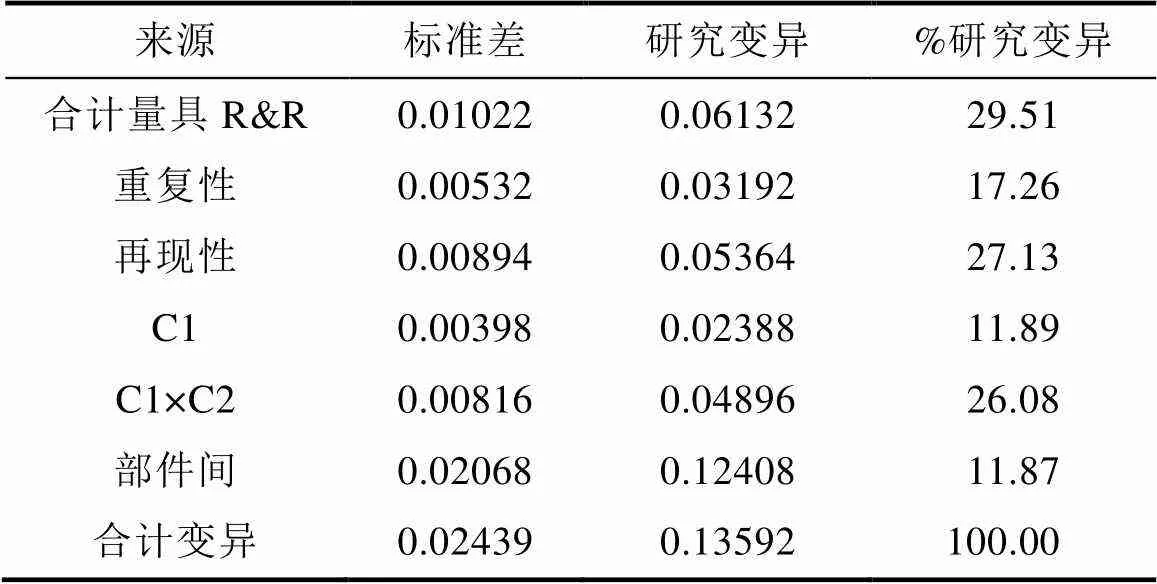
Tab.8 Variation tolerance ratio

3 结论

本文对简单线性轮廓与多变量质量特性的复杂多元测量系统进行能力评价研究，并通过量纲分析的方法达到能力评价的应用目的，最后通过一个经典纸飞机的案例来展示检验基于量纲分析的复杂多元测量系统能力评价方法的有效性。从本文的研究过程以及案例的研究结果来看，量纲分析用于简单线性轮廓与多变量质量特性的测量系统进行评价存在很大的优势，通过降维的方法把复杂多元变量简化为一元或二元质量变量特性的测量，进而对其测量能力的评价。案例分析证明了量纲分析方法对复杂多元测量系统能力评价的有效性。

[1] 何桢. 六西格玛管理第三版[D]. 北京: 中国人民出版社, 2014.

[2] Eagle A R. A method for handing errors in testing and measuring[J]. Industrial Quality Control, 1954(3): 10-14.

[3] Grubbs F E. Error of measurement precision, accuracy and the statistical comparison of measuring instruments[J]. Technometrics, 1973, 15( 2): 53-56.

[4] Mandel J. Repeatability and reproducibility. Journal of Quality and Technology, 1972, 4(2): 74-85.

[5] Mander D P, Prins J, Lampe R E. The economic impact of measurement error. Quality Engineering, 1999, 11: 563-574.

[6] Automotive Industries Action Group (AIAG). Measurement system analysis, 4thed. [M]. MI: Betroit, 2010.

[7] Wang F K, Chern H L, Confidence intervals for two-dimensional data with circular tolerance in a gauge R&R study. Quality & Quantity, 2012, 46(1): 55-59.

[8] Majeske K D. Approval criteria for multivariate measurement systems. Journal of Quality Technology, 2008, 40(2): 140-153.

[9] Automotive Industry Action Group. Measurement systems analysis(4thed)[Z]. Miami: Automotive Industry Action Group, 2010.

[10] Amirhossein Amiri, Changliang zou. Monitoring correlated profile and multivariate quality characteristic[J]. Quality and Reliability Engineering International, 2014, 133-142.

[11] Ebadi M, Shahriari H. A process capability index for simple linear profile[J]. International Advanced Manufacturing Technology, 2013, 64: 857-865.

[12] Ghartemani MK, Noorossana R, Niaki STA. A new approach in capability analysis of processes monitored by a simple linear regression profile[J]. Quality and Reliability Engineering International, 2016, 32: 209-221.

[13] Wu XF. An assessment approach for process capability in simple linear profile[J]. Proceedings of the 22nd International Conference on Industrial Engineering Management, 2015, 30 January 2016: 613-620.

AN Analysis of Simple Linear Profile and Multivariate Measurement Mystems Integrating Dimensional Analysis

LIU Xiao-na, CAO Yu, HAN Zheng-chao, ZHANG Yi

(College of mechanical and electrical engineering, Kunming University of Science and Technology, Kunming 650504, Yunnan)

Measurement system analysis is one of the main contents of statistical quality improvement or control. At present, multivariate analysis of variance or principal component analysis methods are applied to analysis and evaluate multivariate measurement systems. In the actual production process, there are complex multivariate measurement systems with simple linear profile and multivariate quality characteristics. However, few studies have been done on the evaluation of measurement system capability for this complex multivariate quality characteristics. In this article, a method for evaluating the capability of complex multivariate measurement systems based on dimensional analysis is proposed integrating physical and statistical analysis. The method of dimensional analysis in physics is used to study the physical relationship among the related variables of products or processes. The problem of measurement system is transformed from multivariate into univariate measurement system and statistical methods and indicators are used to evaluate the capability of measurement system. Finally, the paper reproduces the classical paper aircraft test, and analyzes and evaluates the measurement system of the paper aircraft by using the proposed dimensional analysis method to verify the effectiveness of the method.

Measurement system analysis; Measurement system capability evaluation; Simple linear profile; Dimensional analysis

TP202+.1 20

A

10.3969/j.issn.1003-6970.2018.11.032

刘小娜(1993-)，女，研究生，主要研究方向：质量工程与质量管理；曹瑜(1992-)，男，研究生，主要研究方向：质量工程与质量管理；韩正超(1994-)，男，研究生，主要研究方向：质量工程与质量管理；张怡(1994-)，男，研究生，主要研究方向：质量工程与质量管理。

刘小娜，曹瑜，韩正超，等.基于量纲分析的简单线性轮廓与多变量的测量系统能力评价[J]. 软件，2018，39（11）：145-150