反舰导弹末制导雷达捕捉移动目标仿真分析

张明亮 张炜 李建华

随着反舰导弹武器技术、战术的不断发展和完善,先进的末制导雷达捕捉和选择技术也得到广泛的应用.末制导搜捕技术在反舰导弹的作战使用中起着至关重要的作用,导弹在超视距反舰作战过程中,首先必须捕捉到目标,才能转入自导并命中目标.因而,导引头对目标的捕捉、识别、跟踪能力是评定反舰导弹武器的重要指标,它有力支撑着反舰导弹的远距离、高精度、全天候以及复杂战场环境的作战.最真实可信的评定方法无疑是采取实弹靶试的方式,但是,由于靶试代价过于巨大,采取各类模型仿真方法进行导引头性能分析评估不失为一种有效的手段[1−2].根据仿真结果,分析评估影响导引头性能的因素以及这些因素对导引头性能的影响途径与程度,进而发现系统存在的问题和缺陷,能够为系统的改进提供依据.基于以上研究背景,本文对反舰导弹末制导雷达捕捉移动目标过程的仿真模型进行探索性研究.

1 反舰导弹超视距打击应用模式

反舰导弹大多采用爆破/侵彻战斗部,其威力范围十分有限,如果命中精度不高,就不能对目标产生有效的杀伤[3].由于超视距反舰导弹发射点、目标点以及飞行轨迹的不确定性,缺少导引头,就无法达到预定精度.在点目标情况下,毁伤力、弹头当量、制导精度之间的关系可由式(1)表示:

式中:K为毁伤力,表征对目标的毁伤能力;W为战斗部的爆炸当量;CEP为圆概率偏差,表征导弹的打击精度.

由图1可以看出,如果设定毁伤力不变,打击精度提高一倍,相应的弹头当量可以减少到原来的1/4;如果设定打击精度从百米级提高到十米级,在弹头当量保持不变的情况下,毁伤力可增加近100倍.因此,反舰导弹要达到预期的作战效果,必须具有精确的末制导寻的能力.

反舰导弹的应用模式通常为“自控+自导”模式[4].为实现反舰导弹的超视距精确打击,必须依赖卫星、无人机、超视距雷达等侦察平台提供的相对可靠精确目标信息.同时,受导弹飞行距离远、飞行时间长及目标机动等因素影响,需要预测判断舰船目标下一时刻的位置.并根据预测判断结果计算、装订射击诸元参数,以保证初始射高和射向的准确性,确保反舰导弹自控飞行段结束,末制导雷达开机工作时,目标在其视场内[5].自导飞行段发现目标前,导弹按预先给定的飞行程序运动、搜索、识别敌方舰艇目标,发现目标后,末制导雷达引导导弹按照导引控制律接近并毁伤目标.

2 末制导雷达搜捕目标方式

导弹末制导雷达在对目标锁定跟踪之前,首先要在一定的范围内对船只目标进行搜索,搜索的目的是为了能够捕获、识别目标,然后转入自动跟踪.通常情况下,反舰导弹的自导飞行段的飞行高度一般在几十米,因此,可近似认为导弹与目标在同一水平面上[6−8].不考虑俯仰与滚动,两者同为质点运动.这样雷达搜索目标时扫描波束的运动可以分解为随导弹一起的平移运动和以末制导雷达为中心的转动,扫描波束的转动受天线扇扫角度的约束,如图2所示.

假设目标位置为T点,t0时刻导弹到达自控终点O,发出雷达开机指令,末制导雷达开机工作.导弹沿OX方向飞行,ON为雷达波束轴线,在雷达开机后从a2位置左右反复搜索,轴线扫描范围为±a3,轴线扫描角速度为ω(t),ω(t)绝对值不变,但方向随搜索时间t作周期性变化.雷达波束宽度为a1,波门前沿为弧cd,波门后沿为弧ab,即abcd构成雷达t0时刻的瞬时视场.为简化模型,本文假设在导弹末制导雷达搜索时间段内,当目标T落入雷达搜索波束的瞬时视场,即可认为末制导雷达捕获并持续锁定目标.在飞行过程中,末制导雷达的搜索波束形成的搜索区域,如图3所示.

3 自控段终点与目标坐标

反舰导弹末制导雷达搜捕目标过程受导弹自控段的终点与舰船目标几何关系的约束.目标落入雷达搜索波束的有效范围内是末制导雷达捕获目标的基本前提[9].因此,确认末制导开机时刻导弹位置以及舰船目标的位置至关重要.

3.1 自控段终点坐标

假设对于所要研究的某型反舰导弹,其自控段终点为圆分布,无系统误差,且已知自控段终点的散布参数圆概率误差CEP.在圆分布条件下,横向偏差∆X1与纵向偏差∆Y1为相互独立的正态随机变量,即∆X1∼N(0,δ1)、∆Y1∼N(0,δ1).圆概率误差CEP与标准差δ1的近似关系为:

则反舰导弹自控段终点(xm0,ym0)的坐标为:

式中,(X1,Y1)为反舰导弹预先设的自控段终点位置.在这里采用虚拟航路法确定自控段终点[10].

3.2 舰船目标坐标

舰船目标在海上机动时,受海区气象、地理、水深、航行经济性、作战任务、作战样式等诸多因素的约束,一般会采用特定的航线和航速,这使得对其位置预测成为可能[11].

假设t1时刻,舰船目标的实际坐标为(X2,Y2),卫星、无人机、超视距雷达等侦察平台对目标进行侦察定位,情报中心将这些侦察情报进行多源融合,向指挥控制中心提供舰船目标位置、速度、航向等情报.毫无疑问,这些情报不可避免存在测量误差.情报测量提供目标的坐标信息为(xt1,yt1),同样其横向偏差∆X2与纵向偏差∆Y2为相互独立的正态随机变量,即 ∆X2∼N(0,δ2)、∆Y2∼N(0,δ2).侦察到目标速度为Vt1,且在定位到自控段结束的时间内速度正负变化的最大值为∆V,移动速度服从正态分布.侦察到目标的航向角为θt1,且在定位到自控段结束的时间内航向角度正负变化的最大值为∆θ,侦察后舰船目标和移动速度服从正态分布,根据正态分布中3δ规则[12],设δv= ∆V/3,δθ= ∆θ/3,目标速度分布在[Vt1−∆V,Vt1+∆V]区间,目标的航向角分布 [θt1−∆θ,θt1+∆θ]区间.

经过一段时间t后,目标相对于初始坐标的运动距离设为R,R同样服从正态分布,即R∼N(R0,δR),其R0=V∗t,δR=V0∗t/3,则经过t时刻,以初始位置建立极坐标,联合概率密度函数由式(4)表示:

随着时间t的增加,舰船位置坐标的不确定性也增加了,如图4所示.要求末制导雷达增大搜索区域,这无疑为末制导雷达捕捉移动目标增添了难度.

3.3 导弹末制导雷达与目标几何关系

假定在t2时刻,导弹的坐标为(xm2,ym2),目标的坐标(xt2,yt2),两者之间的几何关系为:

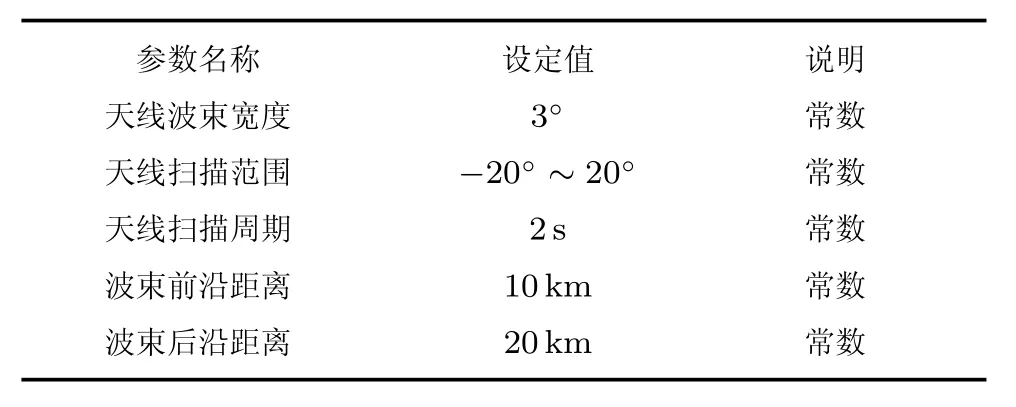
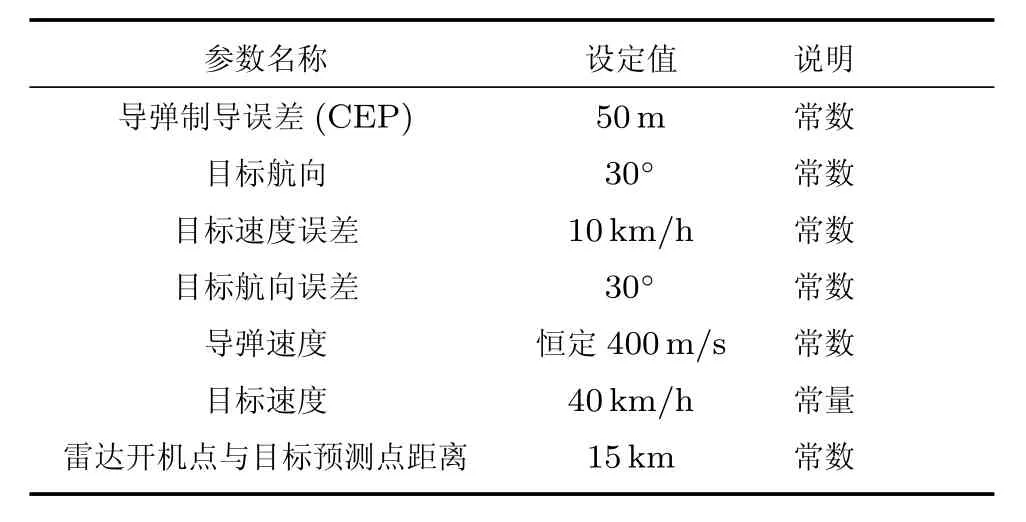
即,当θmt2等于雷达瞬时扫描角度,且loc

为简便计算,本文假定雷达开机搜索扫描阶段,目标是静止不动的.实际上,雷达搜索时间仅为数秒,在该时间内,舰船的移动范围极为有限,相对于雷达的波束宽度可忽略不计.

4 典型反舰导弹末制导搜索模型仿真分析

按照给定的初始条件进行仿真,仿真流程如图5所示,仿真实验主要研究战技指标的变化对搜索概率的影响,为简化研究,部分参数选取了常用的实验值,选取目标定位误差、确定目标至雷达开机的时间间隔、雷达扫描时间等指标为可变参数[13−15].以平均分布为实验设计,实验的各项基本参数设置如表1、表2所示.对每次试验中蒙特卡洛仿真200次,针对仿真实验的结果进行敏感度分析.部分仿真结果如图6、图7所示.其中图6为末制导雷达各时段捕捉目标概率密度分布,图7为雷达搜索概率示意图.

表1 末制导雷达扫描基本参数设定

表2 导弹与目标基本参数设定

表3 可变参数设定

通过多次仿真可知,成功捕捉目标的时间大部分集中于末制导雷达的前4个扫描周期内.对比目标初始位置的测量精度,根据敌方作战意图准确判断敌舰船航迹对提高捕捉概率的影响更为重要.导弹飞行时间与目标航向的变化对捕捉目标概率影响较大,因此,可适当提高导弹的飞行速度,以减少自控段的飞行时间,同时,提高发起攻击行动的隐蔽性,避免敌方舰船在察觉我方行动后大幅改变既定行进方向.增加波束扫描范围虽然也可以提高雷达捕捉概率,但也增加了扫描时间,同时考虑到后续跟踪阶段导弹的侧向过载无法实现大角度转弯,不建议增加雷达波束的扫描范围.

5 结论

当前,自主寻的末制导雷达的设计和作战使用在我国还是一个需要深入研究的重要课题,除了文中提及的战技术指标外,目标特性分析、电磁兼容性、抗干扰性都在不同程度地影响着末制导雷达搜索目标的成功概率,还需要进行更深入细致的研究.