一种基于计算机应用的多周期随机优化问题的求解方法
2018-12-19孙可,刘杰,王战
孙 可, 刘 杰, 王 战
(1. 沈阳师范大学 科信软件学院, 沈阳 110034; 2. 沈阳农业大学 信息与电气工程学院, 沈阳 110866)
0 引 言
随机规划[1-2](SP)是一种处理不确定性的特殊数学规划,它与线性规划(LP)问题密切相关[3]。LP是一个确定性问题,当一些或全部的LP参数包含不确定性时,它就被称为随机规划。 Dantzig首先用不确定的数据[4]阐明了LP的一般问题,因此他被认为是建立SP作为数学分支的先驱。SP的主要优点是,它可以估计不同情况下出现不同的不确定性的概率[5-6]。它扩展了线性和非线性规划问题的范围,包括不同参数的概率性或统计信息。在现实生活中,SP有很多应用,如生产、供应链、调度、游戏、环境等方面都有很好的实现。其中,b.Powell和h.Topaloglu[7]的船队管理模式,Julia l.Higle和Suvrajeet Sen[8]的网络资源利用模型是SP的最典型的应用。
由于SP问题中的变量和条件的不确定性比任何LP问题都要多。因此,用手工计算解决SP问题是很困难的。为了解决这些大规模问题,因此使用分解技术更加合适。可以通过分解子问题和主问题来解决大规模优化问题。本文提出了一种基于分解定价模型来解决SP问题的方法。
在日本,大型市场越来越受欢迎,就像许多其他发达国家一样。由于管理体系和产品质量,人们对超市越来越感兴趣。东京大约有上百家超市,而且这些超市在日本其他城市也有许多分店。在此基础上,通过从大型市场中收集数据,建立了一个真实的生活随机模型。因为用手工计算分析模型是非常困难的。这就是为什么使用数学语言模型分析模型的原因。
1 随机规划问题介绍
在本节中,主要从以下几个方面阐述:定义随机规划问题,基于场景的SP,分解技术。并阐明了子问题的含义,以及分解中使用的主问题,基于分解的技术和步骤。
1.1 SP
首先给出一个线性规划问题,最大(最小)函数z=cTx服从Ax=b,x≥0。m×n维的矩阵A=(aok)i=1,m;j=1,n是等式Ax=b约束的系数矩阵,b=(b1,b2,…,bm)T是等式约束的右向量,c的分量是利润因素,x=(x1,x2,…,xn)T是变量向量,被称为决策变量,且x≥0被称为非负约束。当一些或者所有的LP问题包含不确定性时,即为SP问题。因此,SP问题的数学公式如下:

在本文中,利润因素cω包含不同场景的不确定性,ω和xω代表相应的随机决策变量。SP有不同的类型。其中主要介绍基于场景的SP。
1.2 基于场景的SP
一个随机模型的场景是模型中发生的所有随机事件的结果,以及发生概率的集合。Khan和Weiner[9]是第一个提出源自场景的分析,将场景定义为一个假想的事件序列,将重点放在临时过程和决策点上。有不同类型的SP问题,预期值问题等。在本文中,使用了基于场景的SP 。SP与在任何或所有参数中插入的不确定性的场景相关联,称为基于场景的SP。这种类型的SP问题定义为:


1.3 分解,子问题和主问题
分解是求解大规模LP问题的一种方法。它将整个问题分解成子问题和主问题。有几种类型的分解技术,dantzig-wolfe分解,Bender的分解,三角分解等[10-12]。下面简单地讨论分解技术、子问题和主问题。
考虑到如下线性问题,最大(最小)函数
z=c1x1+c2x2+…+cnxn

具体分解过程如下:
1) 首先从目标函数中减去复杂的约束条件,然后将整个问题分解成以下的子问题;
其中,λ1,λ2,…,λn代表非负的拉格朗日乘数,整个问题就被分解为n个子问题,分别由S1,S2,…,Sn表示。
2) 主问题的生成主要取决于相应的分解技术。本文给出了dantzig-wolfe分解算法的主要问题,以展示分解过程。
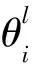
3) 当子问题值之和等于主问题值时得到最优解,即
V(S1)+V(S2)+…+V(Sn)=V(M)
其中,V(S1),V(S2),…,V(Sn)代表子问题的值,V(M)代表主问题的值。
1.4 基于分解的定价方法
这项技术由Mamer和McBride提出。在本节中,简要讨论了基于分解的定价算法。
1) 从原始问题的目标函数中减去约束,把整个问题分解成子问题和主问题。通过删除不提供原始问题的非负值的变量来解决子问题并生成主问题。
2) 当子问题值和主问题值相等时停止。否则,重复前面的步骤。
2 多周期随机模型
在日本,市场管理委员会必须从国家不同的地方收集各种各样的货物,并制定一个预算和一个计划来最大化利润。他们必须为所有商品和其他行业制定预算,有自己的库存和运输设施且必须在不同的时间进行几次外出采购来收集货物,但他们的利润一直都不确定。由于一些不确定的事件,如政治条件、商品价格、客户需求等,可能会发生变化。文章已经收集了2014年的数据。一年分为4次,每段时间包括3个月。将“一月至三月”为第一期,“四月至六月”为第二期,“七月至九月”为第三期,“十月至十二月”为第四期。收集了12种不同产品的数据,包括大米,小麦,豌豆,糖,虾,鱿鱼,香蕉,鸡肉,鸡蛋,牛肉和羊肉等。考虑了他们的运输成本,包装成本,采购成本,人事成本,持有成本。考虑了3种不同情况下的不确定局势“政治条件”。这种不确定的因素妨碍了收集货物,造成运输问题,缺乏客户安全等。所考虑的情形是“良好的政治条件”,“正常的政治条件”和“恶劣的政治条件”。在良好的政治条件下,没有政治障碍和安全的客户,在正常的政治条件下,没有政治障碍,但仍然缺乏安全的客户,以及在恶劣的政治条件下,政治障碍和客户缺乏安全。成本单位是100吨。
首先介绍一些参数、决策变量和公式。
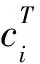
3 算法具体过程
在第一步中,初始化参数的迭代次数,然后讨论Lagrangean乘数的选择过程[13-15]。在此之后,将整个模型分解为子问题和主问题。
1) 设置迭代次数k;
2) 选择一组初始价格的集合λk;
3) 解决子问题;
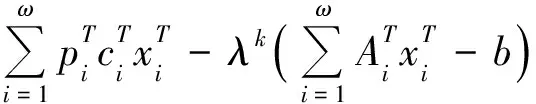
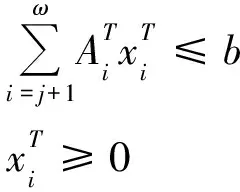
其中,j代表复杂约束,ω是场景数量,t是时间周期。
4) 主问题将通过删除那些没有非负值的变量来从原来的问题中产生。解决以下受限的主问题。
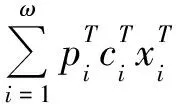
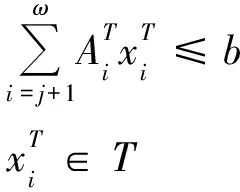
其中,I是一个非空集,所有变量在子问题中给出非负的值。
5) 迭代停止条件,有2种方法。
当子问题的目标值和受限的主问题相等时,停止迭代,即V(Sk)=V(Mk+1)。否则,k=k+1,返回1)。
当没有新的变量进入受限制的主问题时,停止;否则,返回2)。
4 实 验
展示了3个不同场景下的不同周期内的利润比较,如图1所示。
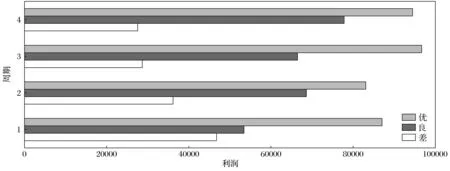
图1 利润比较Fig.1 Profit comparison
在图1中,下面、中间及上面的柱形分别代表了差、良、优的政治状态的场景,每个图表对应的值代表每个场景的利润。例如,87 254美元的数额代表了在第一时期的情况良好的政治状况和其他情况下所获得的利润。金额是以美元计算的。自然的政治条件是企业组织的一个关键因素。直接影响到它的损益。从上面的数字清楚地看到,在每个时期,当政治状况保持良好时,利润最高。同时,由于糟糕的政治状况,利润逐渐减少,如果利润减少,对公司来说将是非常可怕的。从图中可以看出,对于正常的政治状况来说,利润的变动率并不太高,但这很好,如果政治状况持续一年,公司就不会亏损。通过对整体利润的分析,发现在第4期利润最高的是在10—12月,94 712美元。最后,可以预测,该公司必须谨慎坏的政治条件,必须采取一些计划,比如提前收集商品不生的或增加的库存数量的传统位置等,因此它们没有下跌风险在这种情况下,并没有下令迟延交付客户。
5 结 论
本文提出了一种解决多周期SP问题的新方法。为了开发这种技术,使用了DBP的概念。建立了一个模型,分析了日本大型市场的商业政策。收集了一年的数据来开发这个模型。在此基础上,给出了模型的具体表达式,并给出了算法的求解过程。通过对利润的比较,并预测,像大型商店这样的公司必须制定一个多变量计划来减少风险以避免损失。
