原子模拟金属锆中点缺陷行为

2018-12-19邓玉福王钰鑫徐东生

沈阳师范大学学报(自然科学版) 2018年4期

邓玉福, 王钰鑫,3, 何燕,3, 王皞, 徐东生

(1. 沈阳师范大学物理科学与技术学院, 沈阳 110034; 2. 沈阳师范大学辽宁省射线仪器仪表工程技术研究中心, 沈阳 110034; 3. 中国科学院金属研究所, 沈阳 110016)

0 引言

目前对具有六角密堆(HCP)晶体结构金属的物理冶金的研究,部分来自于它们所表现的各种各样的物理和机械性质。理解原子过程、微观结构和性质之间的联系可以为这些材料的新应用开辟道路。锆合金作为包层材料在核工业中有着广泛的应用。在核反应堆中,它们受到快中子通量的作用,导致产生大量的点缺陷,包括空位和自间隙。这些点缺陷随后扩散,并可被系统的不同阱捕获,或者聚集形成更大的缺陷,例如位错环和空位团[1]。空位团也可以出现在淬火锆合金中。

过去已经进行了大量的实验研究来确定HCP-Zr及其合金中这些缺陷团簇的结构。第一个辐射生长模型是在1962年提出的,之后相继又提出了很多模型。然而,能够预测纯Zr的单晶变形的机械模型尚不清楚,因此还是依赖唯象的方法[2]。对诸如锆合金等各向异性材料的基本蠕变机制的理解还不够强,不能真正预测。实验[3-8]研究证实,中子辐照增加了强度和硬度,但随着中子剂量和辐照温度的变化,延性降低。这些力学性能的变化已经从缺陷微观结构演变的角度得到了广泛的解释。近年来,基于密度泛函理论(DFT)进行了多种计算,研究了空位对Zr力学性能的影响[9]。Olsson等[10]计算了含空位锆的弹性常数。他们发现C11、C33和C44增加,而C12和C13减少。报告了由于空位的存在导致的不稳定堆垛层错能的增加和表面能的降低,这表明延性的降低。朱雪燕等[11]通过DFT计算,系统地研究了空位对α-Zr力学性能的影响。同时Celine等[12]也通过ab initio方法给出了金属锆中小空位团簇的可能构型,以及Samolyuk等应用第一原理给出了金属锆中间隙原子的可能位置等。因此,了解点缺陷对材料力学性能的影响,对于揭示辐照下材料力学行为变化的基本机理具有重要意义。

尽管已有大量针对锆的缺陷行为研究,但基于高通量[13]原子构型搜索,并结合蒙特卡洛模拟,实现具有原子分辨率的宏观时间尺度下的点缺陷行为研究,目前相关工作还比较少,对于点缺陷形核长大的整个动力学过程还缺少完整理解。本文采用激发弛豫算法[14-16]得出锆中不同尺寸的空位团簇及间隙团簇的稳定和亚稳定构型,系统地研究了不同尺寸之间稳定构型及亚稳定构型之间的联系。揭示了锆中空位团簇和间隙团簇稳定构型的空间分布特征,并发现一种包含五间隙的团簇构型可以更稳定的存在于金属锆中。

1 方法

摸拟采用Mendelev等[17]的EAM合金势函数,该势适用于金属锆,可较好地描述金属锆的点缺陷包括空位和间隙,在Celine等应用ab initio 算法比较势函数时已经得到了证实。金属锆点缺陷空位及间隙形成能、结合能等计算采用Mousseau提出的单端特征向量跟踪方法即激发弛豫算法(ART activation-relaxation technique)[18-21]。首先建立包含4 000个原子的模拟晶胞,然后在相邻位置依次删除或者添加原子形成空位团簇或间隙团簇,再将此构型弛豫到最低能量并作为初始构型,应用ART方法进行高通量搜索得到一系列稳定及亚稳定构型,保留其中形成能低于2 eV的构型,其中能量最低的构型即为该尺寸下最稳定的空位团簇或间隙团簇构型。

2 结果与讨论

2.1 空位团簇构型及结果

由于六角金属锆的晶体结构空间对称性较低,其空位团簇构型会随着空位数目的增加而变得复杂。对于单空位,只存在一种可能构型,而对于双空位,搜索到2种近邻线性结构,空位在基面分别沿〈1000〉和〈0100〉方向近邻,并且能量相近。然而随着尺寸的增大,团簇结构数目的急剧增加,并且由于局部原子驰豫,它们的稳定性变得非常难以预测。采用ART鞍点搜索法可以搜索到所有相对稳定的构型。同时,各数目空位团簇构型中,最稳定构型也呈现出了一些规律。三、四、五和六空位的几种稳定构型见图1,其中空位和自间隙原子分别用空圈和红色实心圆表示。各空位团簇的结构及其平均形成能见表1。图1中,V3(a),V4(a),V5(a),V6(a)分别为最稳定的空位团簇,其各自的平均形成能在各自空位团簇构型中也最低(见表1中黑斜体)。这种能量最低的构型也称为最稳定的构型。

在三空位中,最稳定构型V3(a)中3个空位分布在同一基面上且彼此最近邻。V3(b)的构型呈线性结构,激发能与V3(a)相同,但是能量稍高。四空位中,最稳定构型V4(a)为空间四面体呈空间旋转对称分布,其余2种构型均为四面体构型,但是构型分布不对称且能量较高。V5(a)是五空位的最稳定构型,其分布也呈现空间旋转对称性。

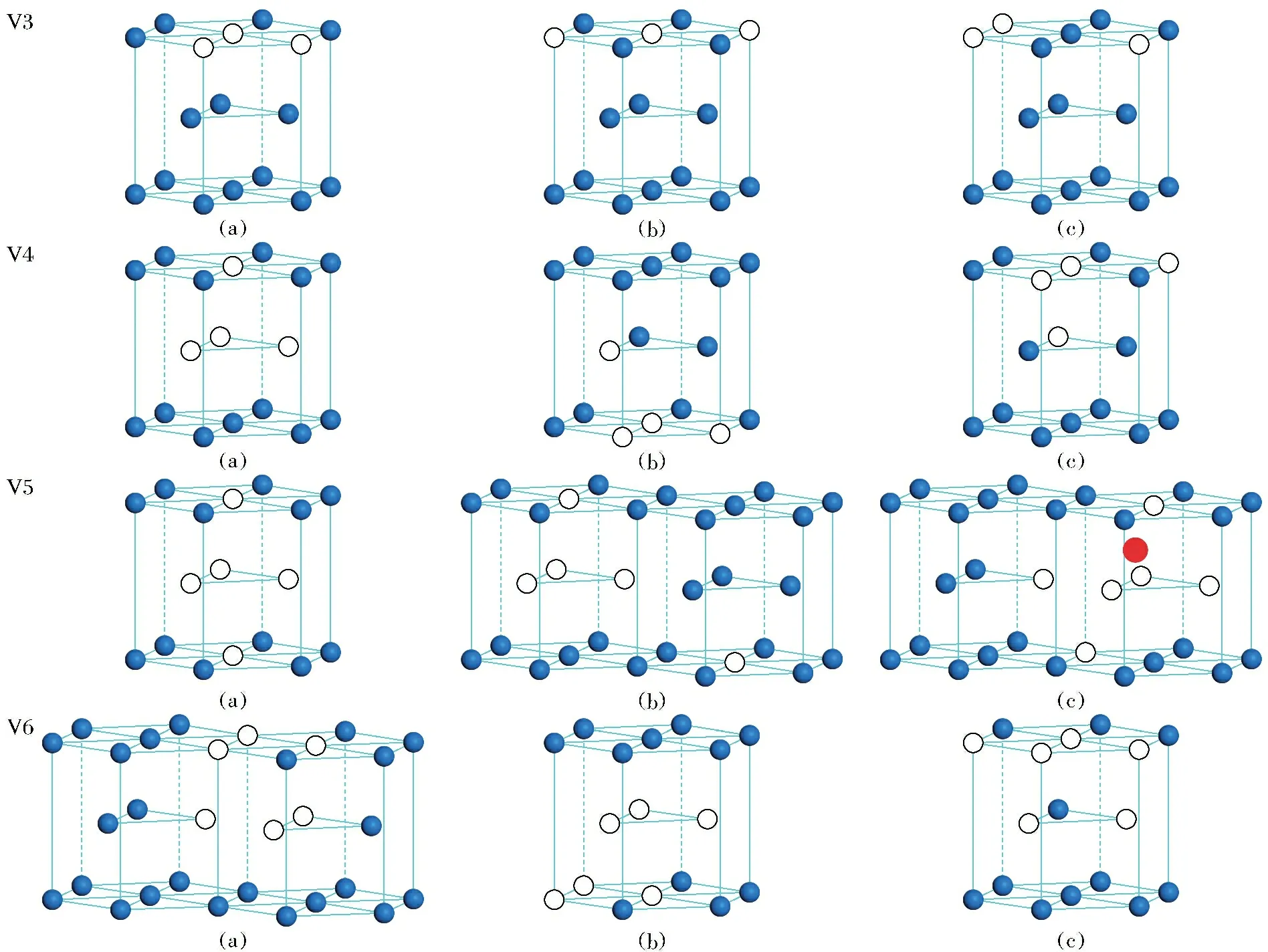
图1 包含空位数为3～6的空位团簇部分相对稳定构型Fig.1 The relative stable configuration of the vacancy cluster with a vacancy of 3～6

随着研究空位数目的增大,发现一些规律。中等数目空位的最稳定构型中能够发现小数目空位的最稳定构型,也可以说较大空位团簇构型是由小数目的最稳定构型组成的。如图1中,空位数为6的最稳定空位团簇构型中包含两个最稳定的3空位团簇,并且呈现空间轴旋转对称性。V6(b)中也是由两个最稳定的3空位团簇组成,但是此构型缺乏对称性能量较高。计算结果见表1。七空位最稳定构型(见图2)中,包含两个最稳定的3空位团簇和一个单空位,也可看成由一个最稳定的6空位团簇和一个单空位组成。通过以上分析,对于中小数目的空位团簇,中等数目的稳定空位团簇由小空位数目稳定团簇组成,可见小数目空位的最稳定构型能够稳定的存在于中等数目的最稳定空位团簇中,并且空位数目合适时呈现旋转对称分布。

空位数由小到大的过程中,最稳定的团簇构型也从平面结构变成3D的空间结构,因为3D结构中团簇是最紧凑的,因此最近邻的空位间有最大的吸引力,并且大部分构型都呈现出对称的分布特征,这与Celine等[12]的计算结果一致。为了更加清晰地表示空位团簇的稳定性,计算了各团簇的单空位和双空位的结合能(见图3)。图3中绘制了各数目最稳定团簇的平均形成能曲线图以及对应的结合能曲线图。其中B1表示单空位结合能,B2表示双空位结合能,F表示平均形成能。一个单空位与一个双空位和VN团簇的结合能的定义为:

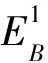
图3 空位团簇最稳定构型的形成能和结合能Fig.3 Formation and binding energies of stable vacancy clusters

在锆中,五、六空位的单空位、双空位结合能明显高于其他数目最稳构型,并且形成能也相对较低。可以看出五、六空位最稳定团簇构型要比其他数目的最稳构型较易形成并且能够更加的稳定存在。

2.2 间隙团簇构型结果

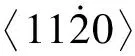
表2 包含间隙数为4～6的间隙团簇各稳定构型的平均形成能Tab.2 Formation energy of clusters with 4 to 6 vacancies

中小数目的间隙团簇的最稳态构型,均呈平面结构且对称分布。并且在中等数目的间隙团簇构型中也能够找到小数目的间隙团簇构型,如图4中五间隙(c)中a构型由四间隙(b)中a构型和一列挤列子构成,六间隙(d)中a构型由四间隙的a构型和两列挤列子构成。对于亚稳态构型也存在一些规律,研究发现不同数目间隙的亚稳态构型的组成方式类似,如图4中四间隙的构型b由三间隙的a和一个单间隙构型组成,五间隙构型b是由一个四间隙最稳态构型和一个单间隙构型组成。四间隙构型d和五间隙构型c也是同样的构成形式。由此可以看出,通过了解小数目间隙团簇的稳定构型可以近似判断出较大数目的间隙团簇构型。

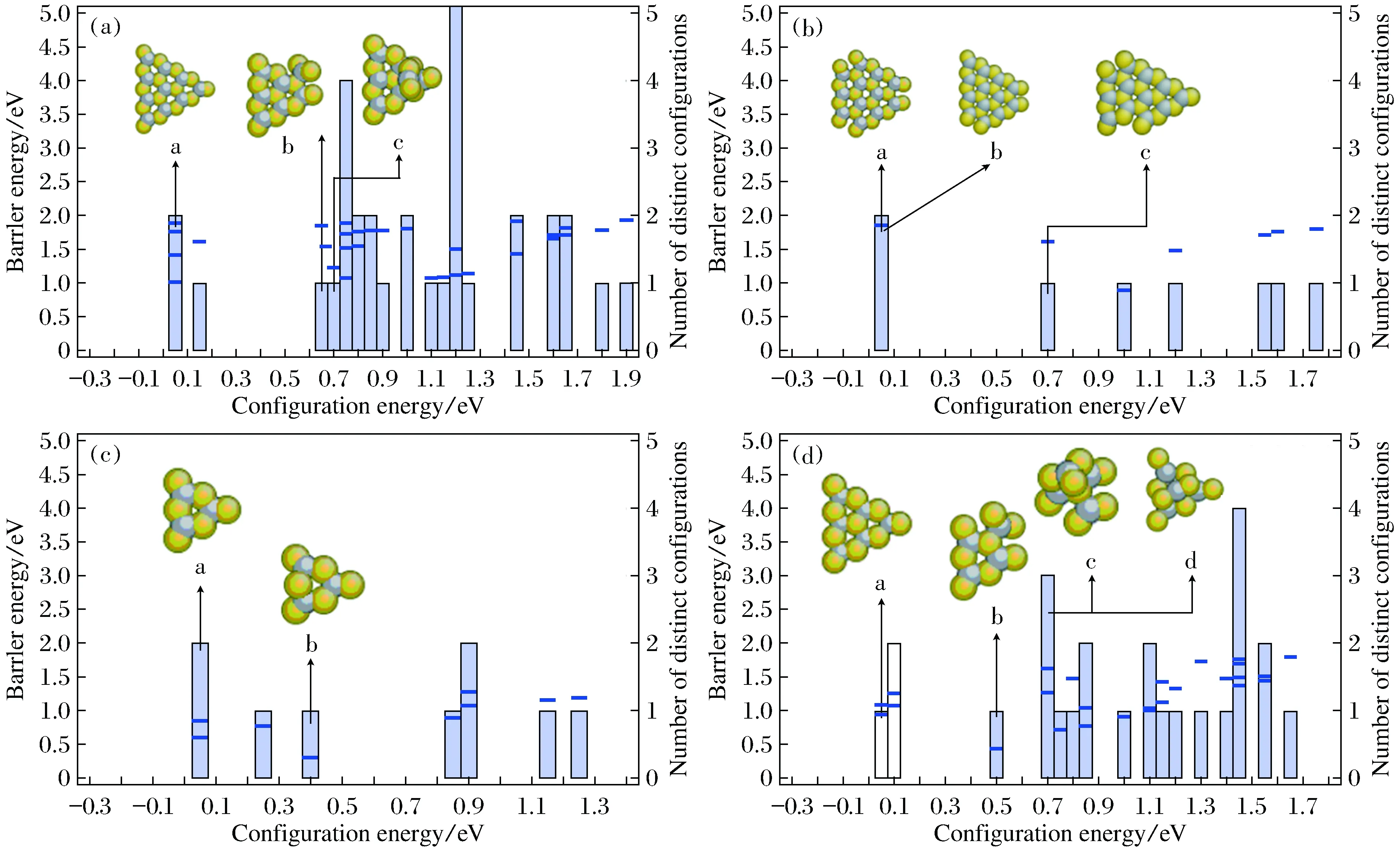
图4 间隙团簇部分稳定构型:(a)、(b)、(c)、(d)分别为三、四、五、六间隙团簇部分稳定构型

图5 间隙最稳定团簇构型的结合能和形成能Fig.5 Formation and binding energies of stable interstitial clusters

为了进一步阐述这些间隙团簇的稳定性, 计算了不同尺寸团簇的单间隙和双间隙结合能。对于每一尺寸的团簇只考虑能量最低的构型,结合能的具体数据见图5。图中B1代表单间隙结合能,B2代表双间隙结合能,F代表平均形成能。从图中可以看出在金属锆中, 在五间隙处单间隙和双间隙结合能都达到峰值, 并且五间隙最稳定团簇的形成能也很低, 可见在中小数目的最稳定间隙团簇中, 五间隙的最稳定团簇构型要比其他数目团簇构型更稳定。