一种新颖的LDPC编码系统码率识别方法
2018-12-19罗路为雷迎科廖锡畅
罗路为 雷迎科 廖锡畅
(国防科技大学电子对抗学院,合肥,230037)
引 言
近年来,在非合作信号处理领域,信道编码识别分析技术成为一个新的研究热点,其在智能通信、信息截获和信息对抗等领域有越来越广泛的应用[1]。在智能通信中已经广泛采用了自适应调制编码技术。该技术可以根据信道质量随时间的变化,随时改变信道编码方式,使其获得最佳的通信效率和服务质量。然而在实际情况中,由于在传输过程中会受到时延、干扰、中断等因素的影响,有时候发送方就不能准时或正确地将相关控制信息传送到接收端,从而造成通信无法建立。这就需要接收方仅根据接收的未知数据快速识别出信道编码的体制、参数,以达到智能通信的目的[2-3]。在各类信道编码方式中,LDPC码具有接近香农极限的纠错能力,以及译码简单,译码错误可检测等优异性能,十分有利于高速信息传输,从而成为了信道编码理论新的研究热点[4]。在下一代5G通信系统中,由于LDPC码较强的纠错性能,可以较好地实现协作中继传输和多小区协作传输。这对LDPC码编码识别算法的研究提出了迫切需求。
针对自适应编码中LDPC码识别技术,国内外已经展开了研究。于明等研究了关于LDPC码码长和码率的识别算法[5],该算法结合信道输出的硬判决接收序列,依次搜索信道编码集合里的全部码长和码率,把伴随式Hamming重量最小的参数组合作为识别结果,但是这种方法需要接收序列中有足够长的无误码序列,因此,在噪声环境复杂的识别过程中该算法的识别性能十分有限,识别效果也不尽人意[6]。为提高算法对于低信噪比信号的识别率,Xia等提出了利用平均校验对数似然比的识别算法[7]。该算法通过对接收序列校验对数似然比求平均值,然后通过设计最大均值判决器的判决门限来对LDPC码进行识别。然而,由于该方法并没有充分考虑数据的可靠度概率信息,对于低码率LDPC码识别时,该方法性能较好;但针对高码率LDPC码,该算法的识别效果仍需要进一步提高。
本文针对现有算法在低信噪比条件下,对LDPC码编码参数识别率低以及对于高码率LDPC码识别性能不足的问题,提出一种利用最大均方比的LDPC码编码识别方法。首先利用信道输出的软信息,将编码校验关系映射到对数似然比域,并定义编码校验对数似然比(Check log-likelihood ratio, CLLR)。然后,分析CLLR模值的统计特性,建立CLLR与待识别LDPC码参数之间的联系。最后,充分利用CLLR在不同校验矩阵下统计特性的区别,找到识别LDPC码编码参数的特征,设计一种综合CLLR均值和方差特征的最大均方比判决器。随后,本文结合IEEE802.11n协议,从算法的可行性分析、均方比判决器的识别性能分析、与原算法的对比分析3个方面,对本文的LDPC码识别算法进行了仿真实验。实验结果显示,在低信噪比环境下,本文算法仍能够高效地完成对LDPC码的识别。特别是在针对高码率LDPC码识别率低的问题,本文算法的识别性能明显优于文献[8]中的算法。
1 LDPC码的编码识别模型
图1给出了本文识别算法所应用的基本通信模型。针对本文LDPC码编码的识别问题,设置调制方式为BPSK,传输信道是噪声功率为σ2的AWGN信道。记码型集合Θ={θx|x=1,2,…,M}为闭集空间的M种LDPC码,其中每一种码型和校验矩阵构成一一映射的关系,与θx型LDPC码相对应的校验矩阵记为Hx,矩阵大小为mx×nx。

图1 识别问题的基本通信模型Fig.1 Basic communication model for recognition problem

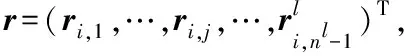
2 基于最大均方比的LDPC码编码识别算法
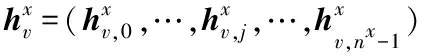

(1)
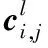
(2)
由Bayes理论,式(2)可以做如下恒等变形
(3)
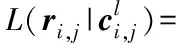
(4)
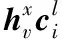
(5)
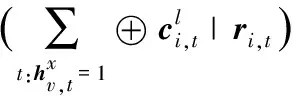
(6)
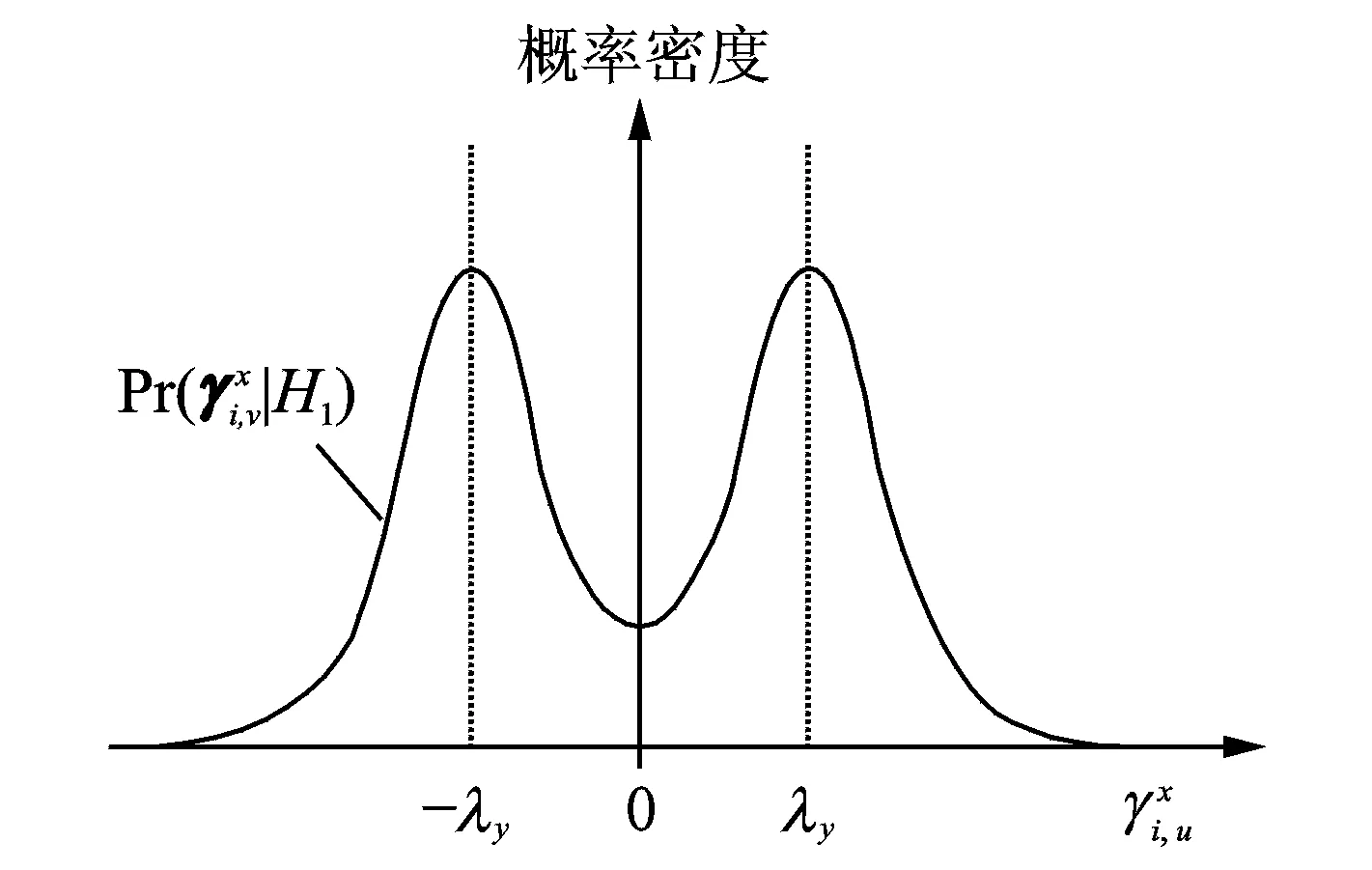
图的概率密度函数示意图Fig.2 A schematic of probability density
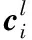
(7)
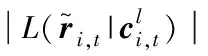
(8)
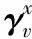

(9)
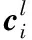

通过以上分析推导,定义最大均方比判决器为
(10)
为了提高识别算法的运算效率,这里采用Hx中部分校验向量定义均方比。记校验矩阵Hx中前p(1≤p≤N)行校验向量定义的均方比φx(p)表示为
(11)
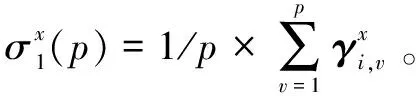
3 仿真分析
通过上文的分析讨论,本节利用Matlab软件进行仿真实验,通过1 000次蒙特卡洛实验,对本文的算法进行实验验证。仿真时,利用IEEE 802.11n协议中的LDPC码以及文献[12]的编码算法,对信息序列进行信道编码。在IEEE 802.11n协议中,LDPC码的编码参数有:码长n=648,1 296,1 944,码率R=1/2, 2/3, 3/4, 5/6[20]。
3.1 利用均方比特性的可行性分析实验
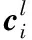
从图中明显可以看出,如果x=l,即编码方式识别正确时,与θl对应的均方比φl(p)明显比其他φl(p)的值要大,而且随着p数量的递增,φl(p)的值将趋近于一个大于1的常数,而其他φl(p)的值则趋近于1,这个结果与文中的理论分析相一致。因此,利用不同编码方式下均方比φx(p)之间的显著差别,可以有效地完成对LDPC码编码方式的识别。
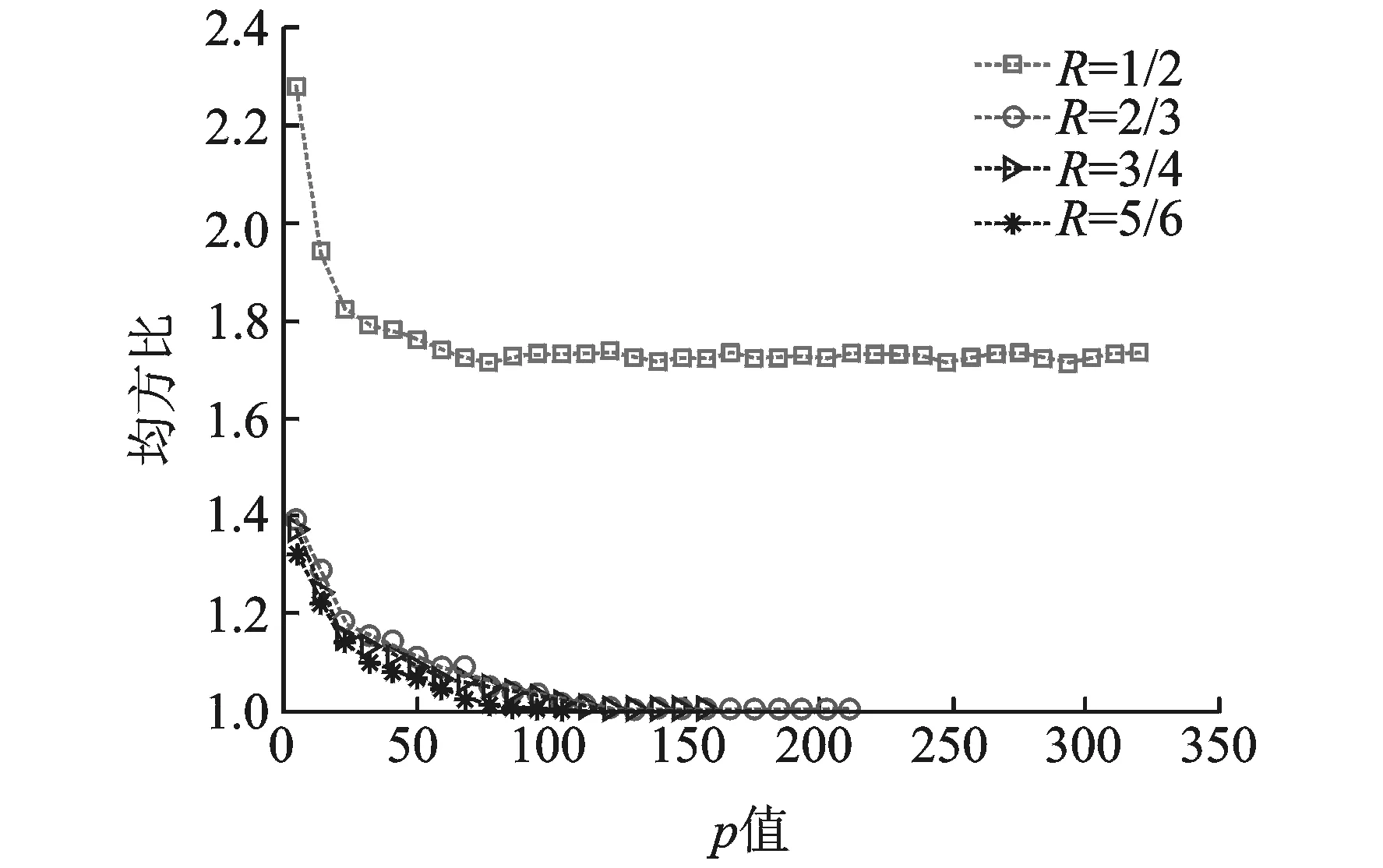
图3 编码方式θ1:n=648,R=1/2时,φx(p)随p取值的变化情况Fig.3 φx(p) changing with the value of p using encoding method θ1:n=648, R=1/2
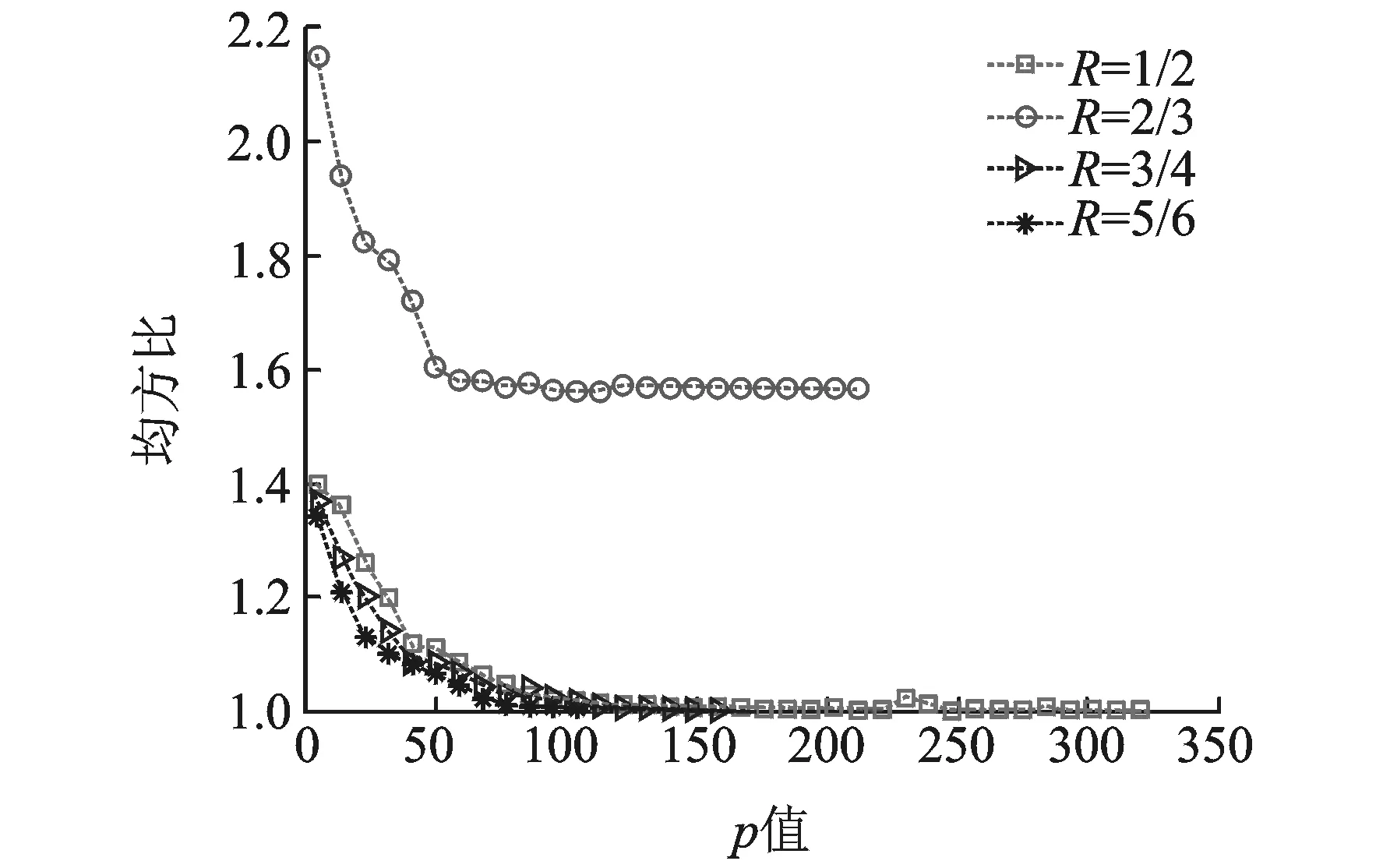
图4 编码方式θ2:n=648,R=2/3时,φx(p)随p取值的变化情况Fig.4 φx(p) changing with the value of p using encoding method θ2:n=648,R=2/3
图5 编码方式θ3:n=648,R=3/4时,φx(p)随p取值的变化情况Fig.5 φx(p) changing with the value of p using encoding method θ3:n=648, R=3/4
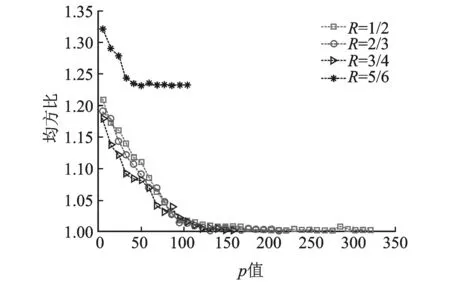
图6 编码方式θ4:n=648,R=5/6时,φx(p)随p取值的变化情况Fig.6 φx(p) changing with the value of p using encoding method θ4:n=648,R=5/6
3.2 利用均方比判决器的识别性能分析
本节通过实验,对均方比判决器的识别性能进行分析。信噪比范围为-4~6 dB,编码参数集合Θ为4种码率下码长分别为648和1 944的LDPC码。图7,图8分别表示码长为648和1 944时,均方比判决器的识别正确率随信噪比的变化情况,此时取p=N。
从图7和图8中可以看出,当信噪比高于4 dB时,码长为648和1 944的任何码率的LDPC码都能够被高效地识别出来,识别率达到99%以上。在信噪比-4~4 dB时,随着信噪比的提高,算法的识别正确率逐渐上升,识别有效性保持较高水平。从图7和图8的对比可以看出,利用最大均方比判决器进行识别,无论是对低码长的LDPC码还是较高码长的LDPC码都有较好的识别性能。
3.3 与最大均值算法的对比实验
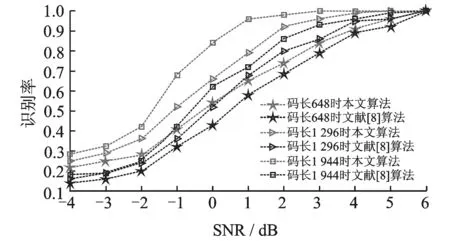
图9 本文算法与文献[8]算法识别正确率变化曲线Fig.9 Recognition rate change curves of the proposed algorithm and the algorithm in Ref.[8]
为考察本文算法在识别高码率LDPC码时的性能,本节将本文算法与文献[8]的算法进行对比分析。实验采用的码率R=5/6,针对3种不同码长,对两种算法LDPC码的识别正确率进行对比分析。仿真中,信噪比范围为-4~6 dB,取p=N。图9给出了两种算法识别正确率的变化曲线。
4 结束语
在信道编码识别体系中,针对现有算法在低信噪比条件下对LDPC码编码参数识别率很低的问题,本文提出了基于最大均方比的LDPC码识别算法。该算法利用信道输出的软信息,将编码校验关系映射到对数似然比域,并定义CLLR。然后,分析CLLR模值的统计特性,建立CLLR与待识别LDPC码参数之间的联系。最后,充分利用CLLR在不同校验矩阵下统计特性的区别,利用最大均方比判决器,进而完成了对LDPC码的闭集识别。该算法综合利用了数据均值和方差的统计特性,有效地避免了传统算法在信噪比低时识别效果不理想的缺陷。而且,针对高码率的LDPC码,均方比判决器的区分度十分明显,进而可达到较为理想的识别效果。最后采用IEEE 802.11n协议中的LDPC码对所提算法进行了仿真实验。同时从利用均方比特性的可行性分析、均方比判决器的识别性能分析、与原算法的对比实验分析3个方面对本文的算法进行实验验证。从实验结果可以看出,相对于已有算法,本文算法在低信噪比环境下仍能获得较好的识别效果,识别增益可达2~5 dB。而且当信噪比高于5 dB时,识别正确率可以达到99%。针对高码率LDPC码的识别,本文算法的识别效果也明显优于现有算法。
