膨胀土分类的PCA-ELM模型及应用

2018-12-19，,2，

长江科学院院报 2018年12期

，, 2，

(1.中南大学资源与安全工程学院，长沙 410083；2.中国人民解放军91292部队，河北高碑店 074000)

1 研究背景

膨胀土是我国广泛分布的一种富含强亲水性矿物的高塑性黏土，素有“工程癌症”之称，常给工程建设带来巨大挑战与危害[1-3]。在富含膨胀土区域进行工程建设时，首先应对膨胀土进行分类，区分其胀缩等级，然后确定工程设计及相应处理措施[4]。若对膨胀土类别进行了漏判或误判，将给工程建设埋下隐患，甚至造成重大灾害事故[1-4]。

国内外关于膨胀土分类主要分为单因素分类法与多因素分类法。单因素分类法简单、易于工程应用，如风干含水量法[5]、塑性图法[6]等。且指标取值往往存在随机性与模糊性，故单因素分类法具有一定片面性，易造成膨胀土类别误判。多因素分类法综合考虑多个指标，一些学者运用模糊数学[7]、多元回归分析[8]、距离判别分析[9]、Fisher判别分析[10]、云模型[11]等进行分析，比单因素分类法更为有效。以上方法取得了一定效果，但由于膨胀土本身的复杂性与相关理论的局限性，目前仍未有一种方法适用于所有的工程环境。

极限学习机(Extreme Learning Machine，ELM)是2004年由黄广斌等[12]提出的一种求解单隐含层神经网络算法。模型简单可靠，无需设置大量网络参数，并具有较快的学习速度、良好的泛化性能和较高的预测精度，已被广泛应用于故障诊断[13]、边坡可靠度分析[14]、电力负荷预测[15]等领域。为此，笔者借鉴极限学习机的思想,并结合主成分分析(Principal Component Analysis，PCA)，提出一种膨胀土分类的PCA-ELM模型。通过采用主成分分析(PCA)对样本进行相关性处理得出变量主成分，以减少极限学习机输入因子，然后构建基于极限学习机的膨胀土分类模型，最后引用相关文献实例验证该模型的可行性。

2 PCA-ELM分类模型

2.1 主成分分析

主成分分析(PCA)是由Pearson提出的一种基于降维思想的多元统计方法，能有效去除样本冗余信息，将多个指标转化为少量相互独立且包含原数据大部分信息的综合性指标[16]。通过对样本数据进行标准化处理，以消除指标间量纲及数值差异，然后计算其相关矩阵特征值及特征向量，得出累计方差贡献率，从而确定样本主成分。计算步骤如下[17]：

(1)对样本数据进行标准化处理。假设样本总数为n，指标总数为p，则样本数据矩阵A为

A=(aij)n×p。

(1)

式中aij为第i个样本的第j个指标值。

原始数据标准化处理后的矩阵A*为：

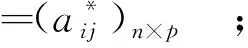
(2)

(3)

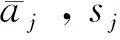
(2)计算相关矩阵R特征值及特征向量，R为

R=A*TA*/(n-1) 。

(4)

求出R的特征值为：λ1≥λ2≥…≥λp，相应特征向量为：μ1,μ2,…,μp。

(3)计算方差贡献率ηi及累计方差贡献率η∑(m)，即：

(5)

(6)

累计方差贡献率是指方差贡献率的累计总和，反映了各指标对因变量的综合影响力，故依据累计方差贡献率确定主成分个数，当累计方差贡献率>80%时，对应的前m个主成分包含样本大部分信息[16-17]。

(4)计算主成分对应的特征向量Up×m为

Up×m=[u1,u2,…,um] 。

(7)

式中ui为各样本主成分特征值，i=1,2,…,m。

则样本主成分矩阵Zn×m为

Zn×m=An×pUp×m。

(8)

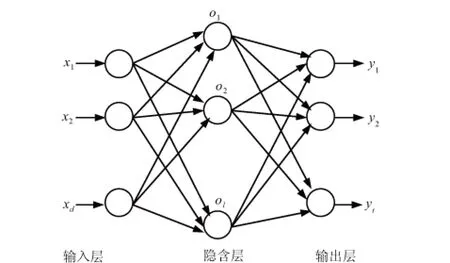
图1 极限学习机网络结构Fig.1 Network structure of extreme learning machine

2.2 极限学习机

极限学习机网络结构见图1[13-15]。该网络由输入层、隐含层及输出层构成，神经元个数分别为d，l，t。图1中xi,oi,yi分别为样本输入层、隐含层、输出层数据。输入层接收样本数据，隐含层通过激活函数对输入数据进行转换，输出层将计算结果输出。计算步骤如下。

(1)初始化ELM参数。随机生成输入层与隐含层权值w及隐含层阈值b：

(9)

b=[b1b2…bl]T。

(10)

(2)计算隐含层输出矩阵H。设隐含层激活函数为f(x)，则H为

(11)

(3)计算输出权值。设隐含层与输出层连接权值v为

(12)

则样本输出Y可表示为

Y=Hv。

(13)

输出层权值v求解模型为

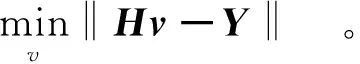
(14)

(15)

式中H+为H的Moore-Penrose广义逆。

可见极限学习机将神经网络转化为矩阵求逆问题，提高了运算速度；且网络参数设置容易，只需预设网络隐含层节点数；同时黄广斌等[12]己经证明其可任意逼近任何连续目标函数，具有良好的泛化性能和预测精度。

2.3 PCA-ELM组合模型

膨胀土分类数据通常存在维数高、数据量大、部分变量间相关性强等特点[4]，若直接作为模型输入，将严重降低计算效率，甚至影响预测结果。因此，通过主成分分析求得能反映样本绝大部分信息的主成分，减少极限学习机的输入，以缩短训练时间，加快收敛速度，提高分类精度。膨胀土分类的PCA-ELM组合模型计算步骤如下：

(1)将膨胀土原始分类数据进行PCA处理，得到新的数据集。

(2)分别将新的数据集划分为训练集和测试集，其中训练集占数据总数的70%，训练集占30%。

(3)将训练集作为极限学习机的输入，并采用十折交叉验证优化极限学习机隐含层节点数，从而得到最优的极限学习机预测模型。

(4)将测试集作为最优极限学习机模型输入，得到分类结果。

将主成分分析与极限学习机组合，结合了两者优势，可很好解决膨胀土分类问题，该组合分类模型计算流程见图2。

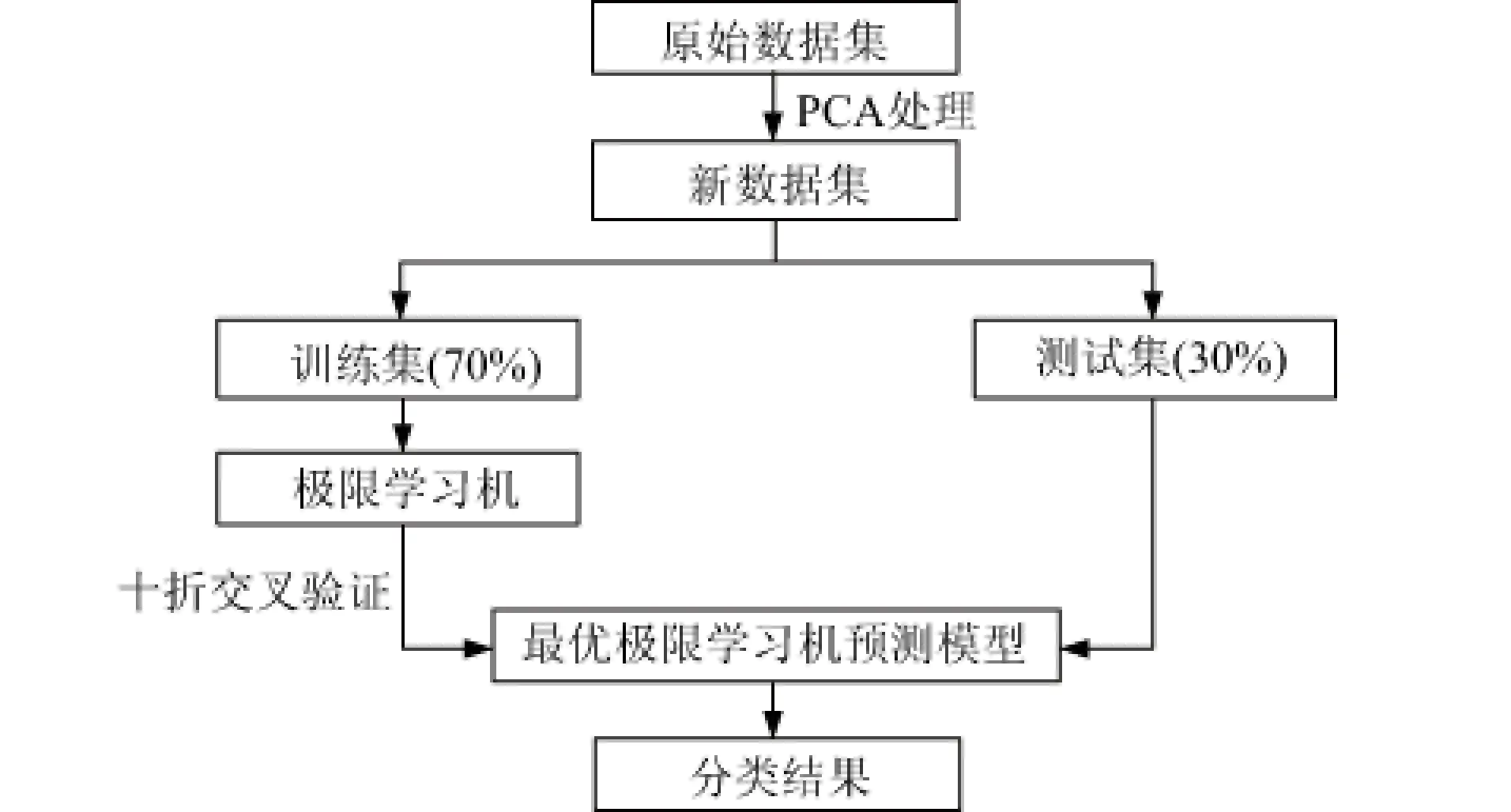
图2 PCA-ELM模型计算流程Fig.2 Calculation flowchart of PCA-ELM model

3 分类指标的选取

膨胀土分类指标可分为直接指标与间接指标[4]。直接指标法直观，如膨胀量、收缩量、矿物含量等指标，但对测试人员专业技能要求较高；间接指标法不够直观，但测试方法简单，并具有一定合理性，如液限、塑限、自由膨胀率等指标。工程中常用间接指标法进行分类。通过对国内外膨胀土分类指标进行统计分析[1-11]，结果表明：液限、塑性指数、粒度组成与自由膨胀率4个指标被选用频率最高。因此，文中选用液限X1、塑性指数X2、<2 μm胶粒含量X3与自由膨胀率X4作为分析指标。

这4个指标中的液限表示土体呈可塑状态的上限含水率，塑性指数表示土体呈塑性状态的含水量范围，两者均与土的粒径组成、黏性矿物含量、比表面积等关系密切[7]；粒度组成是反映膨胀土物质组成特性的基本指标，土中<2 μm胶粒含量越高，表明蒙脱石成分越多，亲水性越强，膨胀性越大[4]；自由膨胀率直接反映土的胀缩特性，黏性矿物含量越高，亲水性越强，自由膨胀率越大[10]。

参考《膨胀土地区建筑技术规范》(GB 50112—2013)[18]、《公路路基设计规范》(JTG D30—2004)[19]以及文献[4]—文献[7]，将膨胀土分为强膨胀土、中等膨胀土、弱膨胀土与非膨胀土4个类别。

4 工程实例

4.1 膨胀土数据集选取

为验证所建立的改进PCA-ELM膨胀土分类方法的有效性，文中以2个膨胀土工程实例进行分析。选取文献[7]中当(阳)—宜(昌)高速公路与文献[10]中合(肥)—六安—叶(集)高速公路共32个膨胀土样本进行分析，样本实测值及类别见表1。

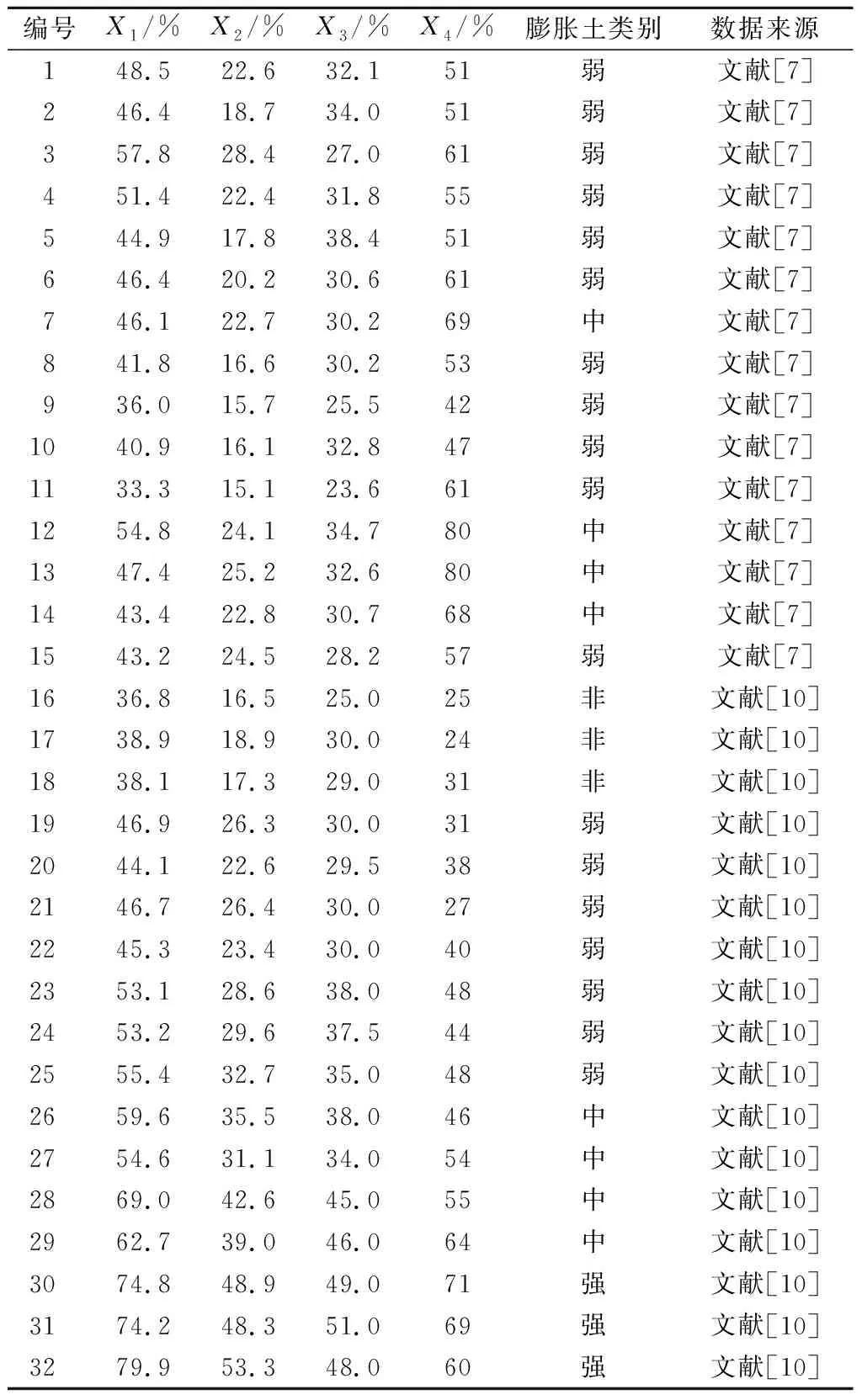
表1 膨胀土实测值及类别Table 1 Measured values and categories of expansive soils

4.2 主成分提取

由于分类指标间存在一定相关性，易造成样本信息输入重复，增加模型训练复杂度，降低泛化性能。因此对各指标主成分进行提取，得到包含样本大部分信息且互无关联的综合性变量。由式(1)—式(6)计算相关矩阵的特征值、方差贡献率及方差累计贡献率，见表2。特征值与成分数的关系见图3，也称碎石图。

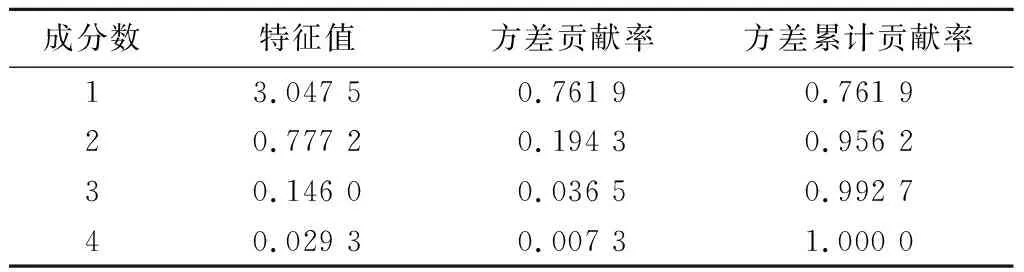
表2 主成分特征值计算结果Table 2 Calculated eigenvalues of principal component

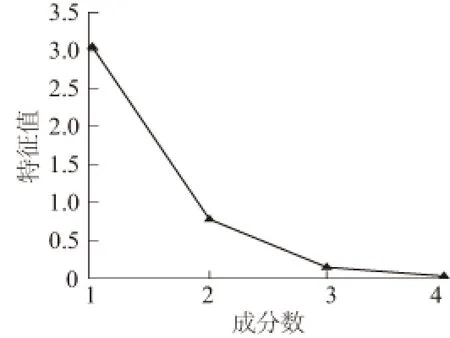
图3 不同成分数的特征值Fig.3 Eigenvalues ofdifferent component numbers

依据方差累计贡献率确定主成分个数，选取前2项主成分进行相关性分析，由此可求得主成分向量为

U4×2=

由主成分向量得出2个主成分的表达式分别为：

F1=0.559 9X1+0.546 2X2+0.536 8X3+0.316 3X4；

F2=0.132 6X1+0.241 2X2+0.173 5X3-0.945 6X4。

依据式(7)和式(8)求得各样本主成分矩阵Z30×3为

4.3 预测结果分析

模型计算过程采用MATLAB软件实现，将主成分作为模型输入，以膨胀土类别为输出。分别选取2个膨胀土工程70%的样本数据为训练集，30%的样本数据为测试集，即当—宜高速公路选取10个为训练集，5个为测试集，合—六—叶高速公路选取12个为训练集，5个为测试集。选取sig函数作为隐含层神经元的激励函数，采用十折交叉验证确定最优隐含层节点数，从而得到最优极限学习机预测模型。由于样本训练集和测试集是随机划分的，且输入层与隐含层权值及隐含层阈值也是随机给定的，故模型输出结果稳定性较差，运行20次，求其平均值。

4.3.1 十折交叉验证结果分析

通过设置不同的隐含层节点数，采用十折交叉验证计算模型分类误差，见图4。由图4可知，当隐含层节点数设定为35时，分类精度达到最佳，且逐渐趋于稳定。故在分析测试集分类精度时，将隐含层神经元个数设为35，此时十折交叉验证精度随运行次数的关系见图5。由图5可知，对于同样的数据输入，进行多次训练，算法输出结果的波动明显，运行20次平均精度为94.20%。

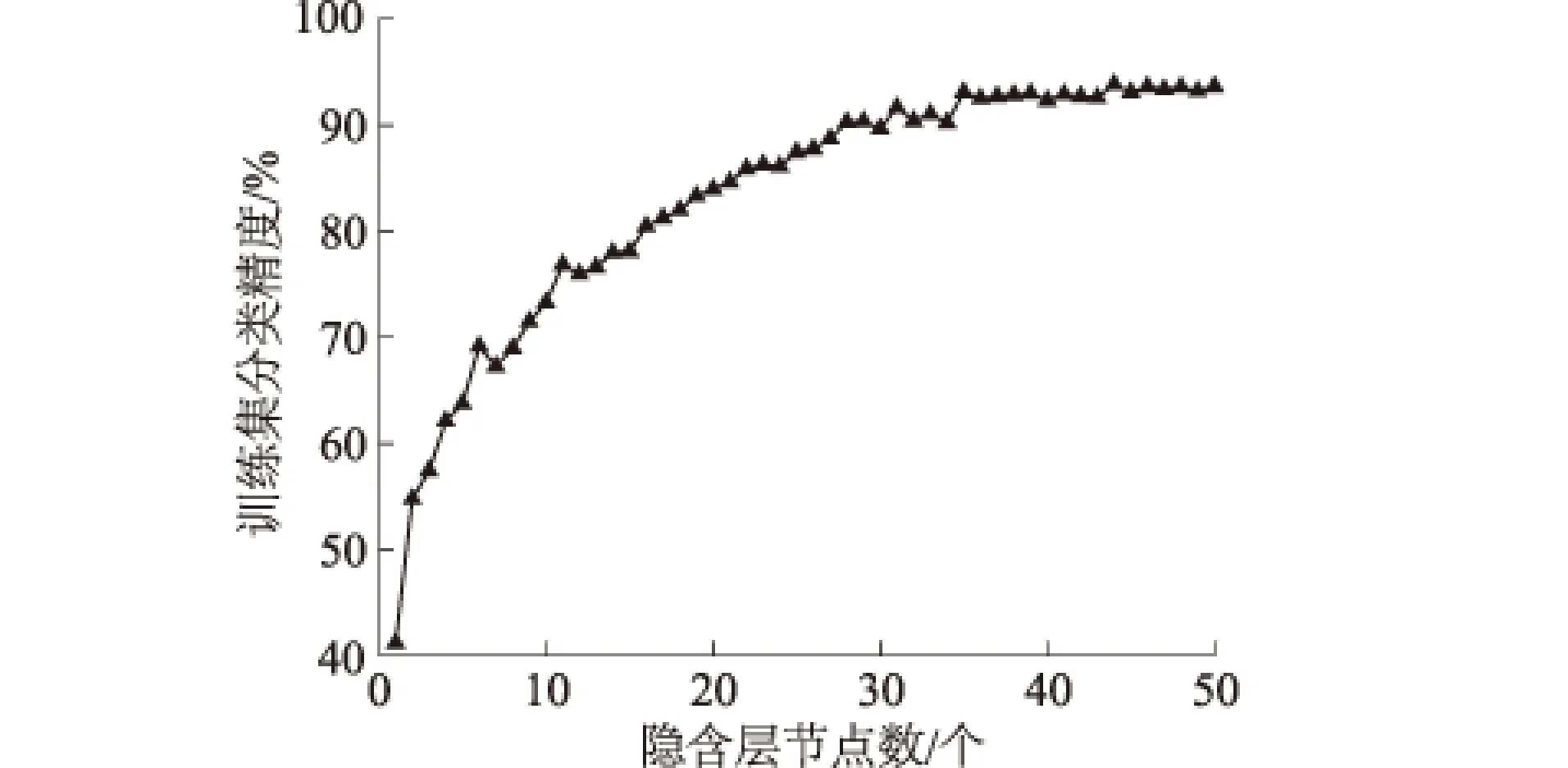
图4 隐含层节点数与训练集分类精度关系Fig.4 Relation between node in hidden layer and classification accuracy of training set

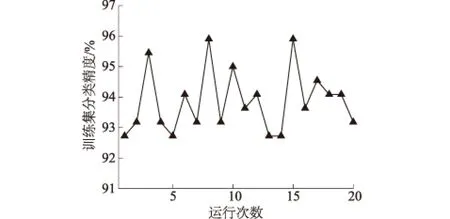
图5 运行次数与十折交叉验证精度关系Fig.5 Relation between running times and 10-fold cross validation accuracy

4.3.2 测试集分类结果分析

将剩余的30%样本数据作为测试集输入至最优极限学习机模型，得到测试集分类结果，见图6。由图6可知，测试集分类精度较高，平均精度为79.00%。

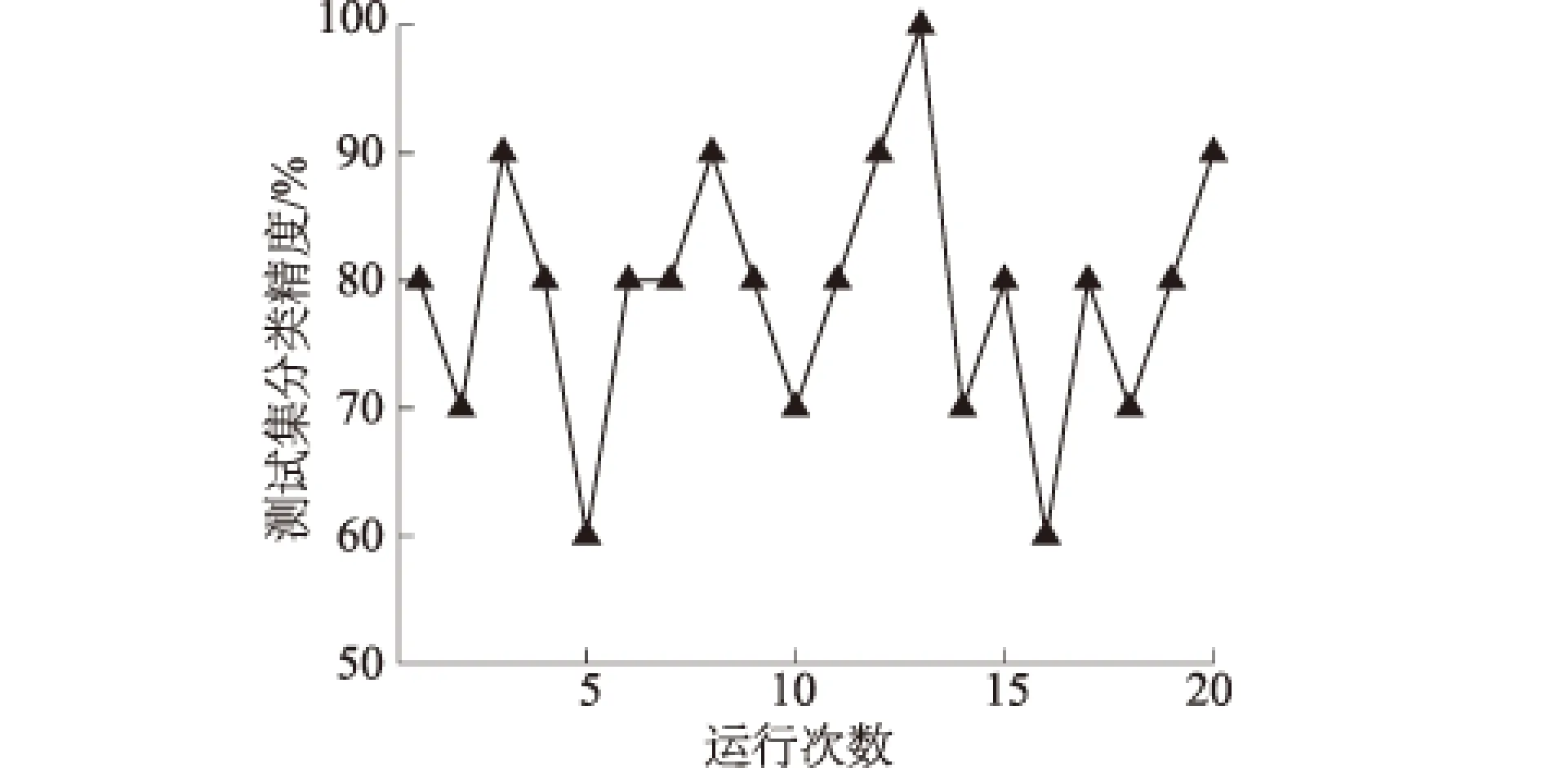
图6 运行次数与测试集分类精度关系Fig.6 Relation between running times and classification accuracy of test set

4.3.3 分类结果对比

同时将PCA-ELM模型与ELM,BP神经网络分类结果进行对比分析，都采用十折交叉验证确定最优模型参数，然后将测试集作为模型输入，得到模型分类精度。通过模型仿真测试，ELM隐含层最优节点数为38，BP神经网络由于需优化参数较多，文中仅进行优化网络隐含层节点数，网络层数同样设置为3层，其他参数均为MATLAB神经网络工具箱默认参数，隐含层最优节点数为9。3种模型训练集和测试集平均分类精度见图7。由图7可知，PCA-ELM,ELM,BP神经网络训练集分类精度分别为94.20%，87.25%，75.67%，测试集分类精度分别为79.00%，77.91%，72.43%，可见，PCA-ELM模型分类精度较高，将其应用于膨胀土分类是可行的。

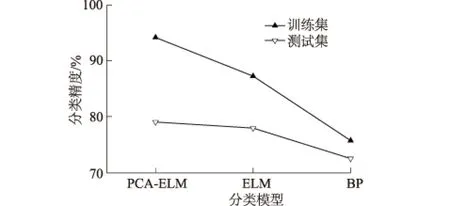
图7 分类模型与分类精度关系Fig.7 Relation between classification model and accuracy

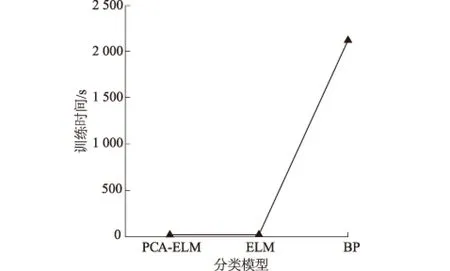
图8 分类模型与训练时间关系Fig.8 Relation between classification model and training time

各分类模型训练时间见图8，PCA-ELM,ELM,BP神经网络训练时间分别为21，24，2 116 s。由于模型训练次数为20次，优化隐含层节点数为51个，并进行了十折交叉验证，故模型迭代循环次数为10 200次，计算量较大。PCA-ELM模型输入变量通过主成分分析降为2个,仅用了21 s完成运算，运算速度非常快，适用于大规模数据的计算；ELM模型训练时间为24 s，由于ELM模型输入变量为4个,大于PCA-ELM模型的输入变量的个数，故ELM模型运算速度稍慢；BP神经网络运算速度最慢，训练时间达到了2 116 s，由于BP神经网络需不断通过反向传播按误差函数梯度方向调整网络权重和阈值，使网络误差平方和最小，故学习效率低，收敛速度慢。