基于遗传算法的RGV 动态调度问题

李新靓，王心如，车东宇，吴宇航

(1. 华北理工大学以升创新教育基地，河北 唐山 063210；2. 华北理工大学理学院，河北 唐山 063210； 3. 华北理工大学数学建模创新实验室，河北 唐山 063210；4. 河北省数据科学与应用重点实验室，河北 唐山 063210)

0 引言

随着我国科学技术的发展和WTO 的加入，RGV（有轨穿梭小车）应运而生，提高了劳动生产率，而在制造业，调度是实现制造业生产高效率、高柔性和高可靠性的关键，制定合理的RGV 动态调度策略拥有强大的时代背景和现实意义。RGV（有轨穿梭小车）提高了劳动生产率，在制造业，调度是实现制造业生产高效率、高柔性和高可靠性的关键，分别考虑一道工序与两道工序的物料加工形式、正常工作与发生故障的情况，制定合理的RGV 动态调度策略拥有强大的时代背景和现实意义。

1 模型假设

（1）假设人力资源为无限资源，不考虑人力资源的调度影响；

（2）假设工件的任一工序必须在其前道工序完成后才能开始，即前一个工序未完成，则后面工序需要等待，保证同一工件不会同时在两台机器上加工；

（3）假设任一台机器每次只能加工一个工件，且一旦开工就不能中断；

（4）假设各工件经过其准备时间后可开始加工，工件的加工时间事先给定，且在整个加工工程中保持不变。

2 模型建立及求解

2.1 模拟工件到达个数

根据许多研究表明[1]，在一定的时间内，制造车间中的工件随机到达相应的CNC 处理机器的个数可呈泊松分布[2]。利用泊松分布公式可模拟一班次（8 个小时）内加工工件的个数。

设泊松分布系数为λ，任意两个先后到达同一CNC 的工件之间的时间间隔服从参数为λ 的指数分布，则根据泊松分布方程[3]：

其中λ 为工件平均到达率，U 为车间利用率，m 为车间机器数量，μ 为工序的平均加工时间， μg为每个工件的平均加工序数。代入各加工参数得到λ=0.00879，则一班次之内加工工件的个数大约为235 件。

2.2 确定优化系统效率的指标

2.2.1 建立实际生产的指标体系[4]

RGV 动态调度的目标是确定最佳的产品加工顺序，满足装配时间的合理调度，使得加工系统的各性能指标达到最优。RGV 的动态调度的性能指标主要包括：缩短生产周期、降低生产成本、提高生产柔性，基于此目的考虑动态调度的性能指标，如图1 所示：

图1 RGV 动态调动指标体系 Fig.1 RGV dynamic mobilization indicator system

2.2.2 构造优化系统的目标函数

分析实际情况可知，时间的指标T越小，成本C越低，资源R利用效率越高，越符合优化的条件，由此建立RGV 车间生产作业的动态调度数学模型，以及模型的目标函数[5]。

（1）关于时间指标T

包括有生产周期T1、提前或拖延完工时间T2、无效时间 T3。生产周期 T1是指完成所有的装配任务所需的总时间，是反映车间的生产效率的重要的指标之一，1T 计算公式如下：

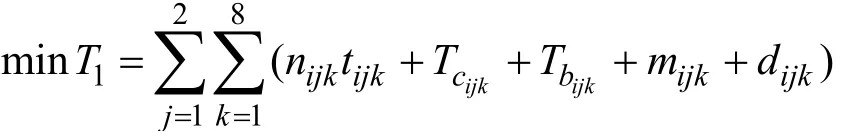
其中，tijk为单位工件的加工时间，nijk为工件规定的生产数量，mijk为CNC 移动的时间，Tijkb为故障修复时间， Tcijk为转移机器的时间，dijk为上一个工件与下一个工件加工的冲突时间。求和部分表示的是装配线完成所有装配任务的完工时间。

提前或拖延时间 T2，客户规定的交货期通常采用时间窗函数，计算公式如下：

其中[ pi, qi]为客户规定的完工时间的区间，T 为产品完工时间即产品在各装配线上最晚的完工时间。

无效生产时间 T3，包括生产准备的时间、产品换加工CNC 的时间、CNC 故障维修的时间等，其计算公式如下：

（2）关于成本C

根据对实际生产的理解，将成本分为原材料的成本 C1、故障成本 C2、人工成本 C3、库存成本 C4、加工成本 C5。

其中cwijk为单个的工件材料的成本，bk为故障率且其值为1%。

其中cmijk为单个工件的加工成本，cgijk为单位故障时间的损失费用。

其中 cf为单个机器的维修费用。

库存成本指的是提前完成的产品其必须保留到交货期而耗用的成本，计算公式如下：

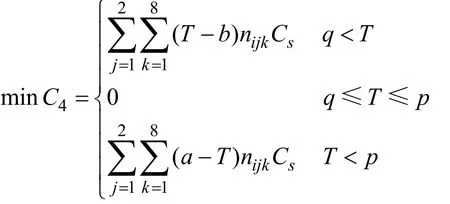
Cs的含义为单个工件的存储费用，a、 b 分别表示规定的取货日期前、后的取货时间。

（3）关于资源指标R

2.3 嵌入贪婪解码算法的遗传算法

算法框图如图2 所示。

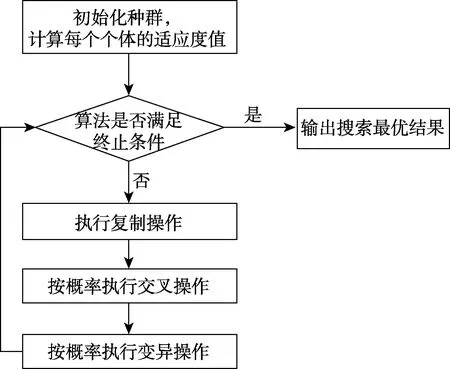
图2 遗传算法的基本过程 Fig.2 Basic process of genetic algorithm

2.3.1 编码

编码就是解的遗传基因[6]，为其的数字化表示，它是在应用的遗传算法实施优化过程中遇到的首要问题，也是应用成功与否的关键之一。在众多编码方法中，目前基于工序的编码方式是最为合理的：编码方式和相对应的解码方案简单，柔性高、容易实现。

图3 解码方式 Fig.3 Decoding mode

2.3.2 贪婪解码算法

将插入式贪婪解码算法，应用到给定的主动调度的反转染色体、反转工艺的路线，就能得到全主动调度[7]。

表1 贪婪解码算法 Tab.1 Greedy decoding algorithm

对于一个给定的主动调度，通过反转该调度，关于工序编码的染色体及解决问题的工艺的路线，按半主动解码方式，对反转的染色体解码，可将原来的主动调度转变成一个新的动态调度，与原主动调度在每台机器上的加工顺序相反。

2.3.3 交叉操作

交叉是遗传算法中的最重要的操作[8]，并决定了的遗传算法的全局搜索能力。采用POX 交叉算法的能够很好地继承父代特征。

图4 POX 算法 Fig.4 POX algorithm

2.3.4 变异操作

通过改进遗传机制中的变异操作来改良遗传算法，使得整个体制可以得到优秀的有效解，所以决定采用基于邻域搜索的一种新型变异算子，它可以保持群体的状态多样性，而且能通过局部的搜索来改善系统的稳定性，提高最优解的出现频率。

2.3.5 选择操作

选择操作的作用是避免有效基因的损失，使高性能的个体更大的概率生存，结合最佳个体保存和比例选择，引入个体竞争，从而提高全局的收敛效率和系统的计算的效率。采用最佳个体的保存和比例选择两种策略的相结合的方式，产生随机数rand∈[0,1]，满足：

2.3.6 适应度函数

将染色体经过交叉、变异等过程变为新的染色体子代，但并不是所有的子代染色体都可以使RGV的动态调度策略变得更满足于给定的指标，提高系统效率。

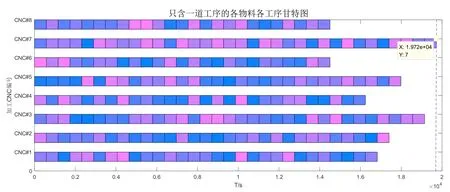
图5 只含一道工序的各工序甘特图 Fig.5 Gantt chart of each process with only one process

对于两道工序的过程，最大完成工时分别为28378 s、35280 s、27482 s。

图6 含两道工序的各工序甘特图 Fig.6 Gantt diagram of each process with two processes

发生故障的时候，两种情况如下：

（1）只含有一道工序时，CNC#6 在12760 s 时发生故障，由求解过程中的输出P 可知，发生故障时第161 个工件正在第六台上加工，工件报废，在发生故障的期间，冻结CNC#6 在发生故障之前的已预约工件202 号与207 号，直至13340 s 时机器设备维修好立即投入使用，以13340 s 为起始点对剩余工件进行调度，由模型求得完成该系统最大完工时为18840 s，知得原工时为19720 s，所以发生故障时的RGV 的动态调度方案对于系统的效率具有促进作用。

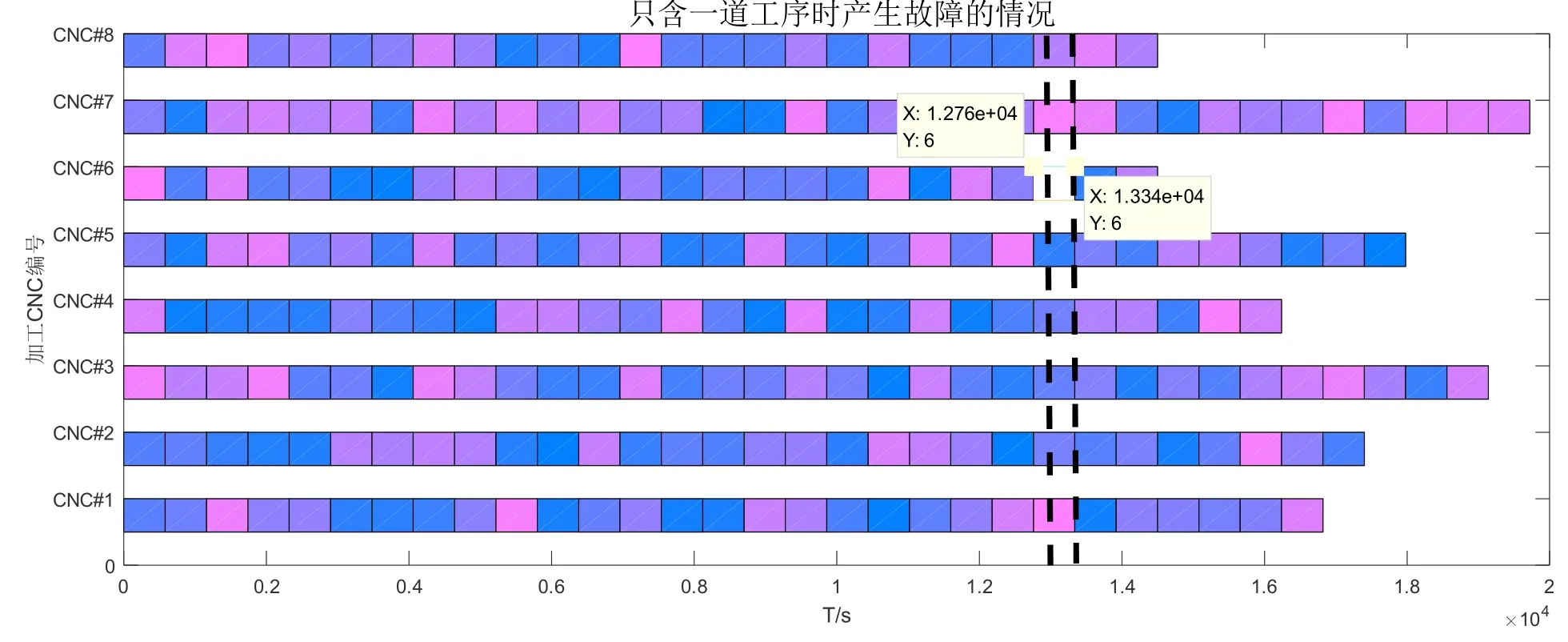
图7 只含一道工序故障甘特图 Fig.7 Contains only one process fault gantt diagram

（2）当系统包含两道工序时，CNC#3 在7560s 时发生故障，由求解过程中的输出P 可知，发生故障时第72 个工件正在第六台上加工，据题意可知该工件报废，在发生故障的期间，冻结CNC#3 在发生故障之前的已预约工件98 号、86 号等工件，直至8400 s 时机器设备维修好立即投入使用，以8400 s为起始点对剩余工件进行调度，由模型求得完成该系统最大完工时为35270 s，知得原工时为35280 s，所以发生故障时的RGV 的动态调度方案对于系统的效率具有促进作用。

图8 含两道工序的故障甘特图[9] Fig.8 Fault gantt diagram with two processes

算法有效性的分析，测试算法的性能，进行仿真及分析。

为测试算法性能，采用柔性车间调度的两个问题Q1（十工件十机器）以及Q2（六工件四机器）和选择能确定性能的加工数据作为算法好坏的指标，构造2 个不相同的RGV 动态调度的测试。且将测试问题看作一般性调度问题，即工序的加工机器与各工序的时间已知，找到工序的最优排序即RGV 的最佳调度策略并输出该系统完成加工固定工件数所需要的最大工时。

提前规定好算法内的参数：最大遗传代数MAXGEN=500，个体数目NIND=20，代沟GGAP=0.9，交叉率XOVR=0.8，变异率MUTR=0.6，分别采用建立的模型和基本遗传算法对每个测试随机计算20次，得到结果如表所示，其中，Tmax，AMN、No.BMN 和AG 分别表示两种算法运行20 次结果后，其中所得的最大完工时，平均的生产周期、得到最优的生产结果的次数以及得到最优解的代数平均值。

表2 改进遗传算法 Tab.2 Improved genetic algorithm

表2 为所得的测试结果，可知改进的遗传算法采用了贪心解码算法以及基于邻域搜索[10]的变异操作后可获得最优生产结果的次数增多，比原来的基本遗传算法的稳定性提高显著；相比采用基本单点式或随机式交叉方式，改进后的遗传算法应用POX 交叉算子进行交叉操作，使其可继承父代优良特征的性能大大提高；改进的算法的AG 指标较大，说明在选择操作过程中结合最佳个体保存和比例选择，有效提高了全局收敛和计算效率，进而说明改进的算法可以较优良的跳出寻找局部最优解，避免早熟收敛。

通过解的变化和种群均值的变化，可见应用改进的遗传算法的收敛性。

图9 解的变化与种群均值变化的过程 Fig.9 Change of solution and change of population mean

3 结论

遗传算法利用简单的编码技术和繁殖机制来表现复杂的现象，仅根据个体个体的适应度值进行搜索，不受限制条件的约束，操作简单且具有高效性、鲁棒性、强通用性等特点。

利用贪婪解码算法优化遗传算法，将搜索空间限于主动调度集，不仅能保证最优调度存在，而且能提高搜索效率。

基于工序编码的染色体只具有半Lamark 特性，遗传操作的设计对算法的性能有较大影响。 一班（8 个小时）内加工工件数约为235 个。选取产品完成时间、生产周期等时间指标，原材料成本、人工成本等成本指标，人员利用率、时间利用率等资源指标作为优化约束条件。应用遗传算法对RGV 动态调度问题进行求解，编码方式应用基于工序的编码方式；插入贪婪解码算法对传统遗传算法进行优化；应用POX 交叉算子进行交叉操作；采用基于邻域搜索的变异操作；在选择操作过程中结合最佳个体保存和比例选择，引入个体竞争，提高全局收敛和计算效率；得出235 个工件一班之内的加工顺序流程。