基于变量控制的太阳影子定位
2018-12-19朱英豪彭杨杨
田 冰,朱英豪,彭杨杨
(1. 华北理工大学数学建模创新实验室,河北 唐山 063210;2. 华北理工大学冶金与能源学院, 河北 唐山 063210;3. 华北理工大学以升教育创新基地,河北 唐山 063210)
0 引言
影子是一种光学现象。光线在同种介质中沿直线传播,不能穿过不透明物体而形成的较暗区域,就是影子。太阳影子定位技术逐渐应用于各个领域,其原理为通过观察物体的影子变化来确定日期时间和物体所在的地理位置。通过建立太阳高度角与影长的物理模型,以及最小二乘法拟合模型,研究出直杆随各参数的变化规律,利用影子顶点坐标,建立数学模型求解直杆所处位置。利用MATLAB 进行最小二乘法拟合,得到影长关于时间变化的函数方程,利用该方程求解图像最低点,从而确定观测点的精确经纬度。
1 太阳影子长度相关函数方程的建立
物体在光线的照射下,会在地面上留下它的投影,这就是影子。物体的影子长短不仅与物体自身体量有关系,还与许多外界因素有关,即位置、日期、时间、太阳高度角等[1]。
对于地球表面上的一个点,太阳高度角指的是太阳光的入射方向与地平面切线的夹角,记作h。随着地球的自转运动,太阳光线与地平面切线的夹角改变,太阳高度角也随之变化。太阳赤纬是地球赤道平面与太阳和地球中心的连线之间的夹角,等于太阳直射点的纬度值,记作σ 。太阳时角时太阳所处的位置与正午太阳位置之间的角度差,记作ε 。地理纬度记作δ 。
在进行模型建立前,首先建立合理的假设条件,简化模型:
(1)假设影子的长度与地形无关;(2)假设大气层分布均匀,对阳光折射率不变。
太阳赤纬δ 的计算公式为[2]:

图1 太阳相关角的图像 Fig.1 Image of solar correlation Angle

其中N 为积日,即日期在年内的序号,int 表示取整数。
太阳时角ε 的计算公式为[3]:

太阳高度角的计算公式[3]为:

设物体自身高度为l,影子的长度m,由三角函数可知:

由计算公式可以看出物体影子的长度与太阳高度角有着直接的关系,而随日期变化的太阳赤纬、随时间和经度变化的时角都影响着太阳高度角,所以物体影子的长短与自身长度、日期和时间、当地经纬度有关。
2 影长随各参数变化的模型建立
2.1 影子长度随地理纬度的变化规律
在影响太阳高度角的这些因素中,首先控制日期、时间、经度不变,仅物体所处的地理纬度改变。为便于研究,设定日期为问题1 给出的2015 年10 月22 日,物体长度为3 米,时间选取正午12 点整,代入公式求解得到影子长度随纬度变化的关系式:

利用MATLAB 绘制出影长随地理纬度变化的曲线为:

图2 影长关于纬度的变化曲线图 Fig.2 Change curve of shadow length with respect to latitude
总结规律为:当物体的日期时间和经度确定,随着地理纬度的升高,影长逐渐增加。
2.2 影子长度随时间的变化规律
研究了影子长短随纬度变化的规律后,控制日期和经纬度不变,研究物体影长关于时间的变化规律。仍以问题1 中2015 年10 月22 日天安门广场3 米高的直杆为参照,研究北京时间9:00-15:00 的影子长短变化,计算得到影子长度随时间的变化规律为:

当ε∈[9,15]时,计算出部分影长如下表:

表1 部分时间对应的影长 Tab.1 Corresponding shadow lengths of part time
利用MATLAB 绘制出影长及太阳高度角随时间变化的曲线为:

图3 影长及太阳高度角随时间的变化曲线图 Fig.3 Curve of shadow length and solar altitude Angle over time
总结规律为:当物体的高度和地点确定,在一天之内,从早上开始影长逐渐减小,减小的速度越来越慢,到正午12 点时影长最短,从正午到傍晚时,影长不断增加,增加的速度越来越快。
2.3 基于曲线拟合的经度求解
根据某一时刻物体影子的顶点坐标x 和y,可以得出这一时刻影子长度为:

利用附件4 中顶点坐标数据可以计算出14:42 到15:42 这一个小时内不同时刻的影子长度。在问题1 中,最终求得的影长随时间的变化曲线为抛物线,于是利用这一个小时的影长与时间的数据,在MATLAB 中对影长和时间进行抛物线拟合[4],得到曲线方程为:

图像最底点处即为导数值为0 的点,也是当地正午12 点对应的影长,对方程(8)求导可知在北京时间12.6 小时的时候影长取最小值。

图4 影长随时间变化的拟合曲线图 Fig.4 Fitting curve of shadow length changing with time
由地理知识可知,影子最短的时刻对应于一天的正午12 点,此点对应的北京时间为12.6,即该地与北京的时差为0.6 小时。所以直杆所处地点的经度为:

3 基于最小二乘法的纬度迭代求解
确定了物体所在地的经度之后,为了确定其纬度,引入太阳方位角,即直杆在太阳光线下的投影与正南方向的夹角γ,其计算公式[5]为:

根据影子定点坐标数据确定实测量方位角为

在物体所在地的经纬度未知时,时角的值不能确定,若利用问题1 建立的若干太阳角数学模型求解纬度,涉及的未知量太多,无法直接求解方程得出结果。考虑到变量个数不为一且范围广,采用寻找最优解的思想,模拟出各种可能的纬度,得到它的方位角,然后与实际值作误差分析,若误差足够小,寻找使模拟出的数据与真实数据为误差最小值时,即为纬度最优解。
在这里采用最小二乘法对纬度进行优化求解[6],太阳方位角和实际方位角的相对误差平方和为:

目标函数为:

约束条件为:
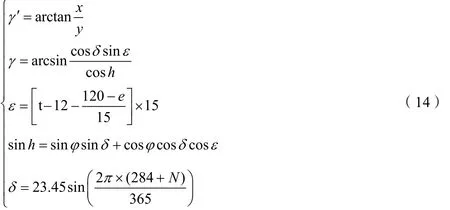
在MATLAB 中进行纬度的迭代[7],设定初始纬度范围是[-90°, +90°],设定步长为20°,计算出满足条件的大致范围,在这些符合条件的区域中重新设定步长为0.5°,继续进行迭代选取出精确到更高的区域后,在这些区域中重复进行迭代,就这样一直择优选取迭代区域,使精度越来越高,直到符合各参数精度要求后结束,确定了误差平方和最小时的纬度为19.50°N 和19.68°N。
所以附件1 影子的数据对应的地点可能为(19.50°N,110°E)和(19.68°N,110°E),在地图上进行定位后如下图:

图5 (19.68°N,110°E)定位图 Fig.5 (19.68°N, 110°E) location diagram

图6 (19.50°N,110°E)定位图 Fig.6 (19.50°N, 110°E) location diagram
4 结论
(1)太阳影子长度变化规律:正午之前,随着时间的推移,影长逐渐减小;正午以后,随时间的推移,影长逐渐增加。
(2)在已知影长随时间变化的图像近似为抛物线前提下,于是根据已有数据确定影长,并对影长和时间进行抛物线拟合,求得影长最小值处所对应的北京时间为12:36,根据两地的时差为36 分钟,求得影子所在地的经度为110°E。以太阳方位角和实际测量方位角的误差为切入点,用最小二乘法逐步选取出更精确的纬度范围,进行迭代确定出符合条件的纬度最优解为19.50°N 和19.68°N。
(3)在建立影子长度变化的数学模型中,分析影子长度关于各参数的变化规律,并在建立3m 高的直杆的太阳影子长度变化曲线中,采用了控制变量法,将多因素问题变为单因素求解问题,使要研究的参数对影长的影响更加显著。
(4)根据某固定直杆在水平面上的太阳影子顶点坐标数据,建立数学模型确定其所处的具体地点和日期的推理过程中,利用曲线拟合思想由已知推未知,并利用迭代求解目标函数最优解,避免了参数不确定性的讨论。问题3 中,未知参数过多,在第2 问的基础上进行多参数、多层迭代,设置的变量范围广,求解的结果也越精确。问题4 中,利用图像分析技术,将图像中有用的数据提取出来,结合现有的问题3 中的模型直接进行求解,使求解过程更加简便。
(5)曲线拟合的思想还可以用在科学和工程上,利用采集的离散数据样本,能都得到一条连续函数或者更加密集的离散样本。图像分析中的图像特征提取能够运用在分类器上分类纹理图像,在信号处理上也有重要作用。
