轮,扇,星和双星的邻点扩展和可区别全染色
2018-12-19陈祥恩王治文
张 辉,陈祥恩,王治文
(西北师范大学数学与统计学院,甘肃 兰州 730070;宁夏大学数学计算机科学学院,宁夏 银川 750021)
0 引言及准备工作
首先,Kalkowski M等人在文献[1]中介绍和研究了图的邻和可区别一般边染色.并且提出著名的1-2-3猜想.其次,Przybylo J和Wo nizk M在文献[2]中进一步提出了邻和可区别一般全染色,且提出著名的1-2猜想.在文献[3]中给出:每一个图都可以用2,3对图的点及边赋权,使得邻和可区别.之后,文献[4]在此基础上提出邻点扩展和可区别全染色,且得出了一些特殊图的邻点扩展和可区别全染色,提出了一个猜想.在本文中我们对轮,扇,星和双星的邻点扩展和可区别全染色进行研究与讨论.
图G的一个全k-染色是指它的全体顶点及边分配的色集合为{1,2,…,k}.
使得图G存在NESD全k-染色中k的最小值被称为图G的邻点扩展和可区别全色数,简记为 egndi∑(G).
文献[5]中给出轮,扇,星和双星的概念,对n+1阶轮Wn,设其顶点集合为V(Wn),其边集合为{vnv1}.将n+1阶轮Wn的边vnv1删去之后得到的就是n+1阶的扇Fn.对n+1阶星K1,n,设其顶点集合为,其边集合为.对2n+2 阶的双星 S2n,设其顶点集为,其边集合为
文献[4]中研究了路,圈,完全图,树等图的邻点扩展和可区别全染色,确定了它们的邻点扩展和可区别全色数.并提出了一个猜想.
命题1[4]设P(mm≥2)是m阶的路,则
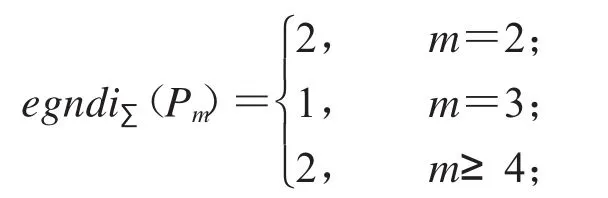
命题2[4]设Cm(m≥3)是m阶的圈,则
命题 3[4]设 T 是 n(n≥2)阶的树,则.
猜想1[4]设G为简单图,则.
引理1[4]设Kn(n≥2)是n阶的完全图,则.
1 主要结论及其证明
定理1设W(nn≥3)为n+1阶的轮,则egndi∑(Wn)=2.
情形1n为奇数
(2)n≥5时:c(v)0=1;c(v2i-1)=1,1≤2i-1≤n;c(v2)i=2,2≤2i≤n-1.除边vn-1vn染颜色2外,其余边均染颜色1.则每个顶点的扩展和计算如下:;w(v1)=7;w(v2)i=6,2≤2i≤n-3;w(v2i-1)=8,3≤2i-1≤n-2;w(vn-1)=7;w(vn)=8.
显然w(v)i≠w(vi+1),vivi+1∈E(Wn)且1≤i≤n-1;w(v1)≠w(vn).下面考虑w(v0)≠w(v)i,1≤i≤n.由于n≥5,可知,而w(v)i≤8,因此w(v0)≠w(v)i,1≤i≤n.故当n为奇数且n≥5时,c是Wn的一个NESD全2-染色.
情形2n为偶数
c(v0)=1;c(v2i-1)=1,1≤2i-1≤n-1;c(v2)i=2,2≤2i≤n.所有边均染颜色1.则每个顶点的扩展和计算如下:,2≤2i≤n.
显然w(v)i≠w(vi+1),vivi+1∈E(Wn)且1≤i≤n-1;w(v1)≠w(vn).下面考虑w(v0)≠w(v)i,1≤i≤n.由于n≥4,可知,而w(v)i≤8,因此,w(v0)≠w(v)i,1≤i≤n.故当n为偶数时,c是Wn的一个NESD全2-染色.
定理2设F(nn≥3)为n+1阶的扇,则egndi∑(Fn)=2.
情形1n为奇数
c(v)0=1;c(v2i-)1=1,1≤2i-1≤n;c(v2)i=2,2≤2i≤n-1.所有边均染颜色1.则每个顶点的扩展和计算如下:,w(v2)i=6,2≤2i≤n-1;w(v2i-)1=8,3≤2i-1≤n-2;w(vn)=5.
显然w(v)i≠w(vi+1),vivi+1∈E(Fn)且1≤i≤n-1.下面考虑w(v0)≠w(v)i,1≤i≤n.假设 w(v0)=w(v1),有,即,与n为整数矛盾;假设w(v0)=w(v2)i,3≤2i≤n-1,有,即,与n为整数矛盾;假设w(v0)=w(v2i-1),3≤2i≤n-2,有,即,与n为整数矛盾;假设w(v0)=w(vn),有,即,与n为整数矛盾.因此,w(v0)≠w(v)i,1≤i≤n.故当n为奇数时,c是Fn的一个NESD全2-染色.
情形2n为偶数
c(v0)=1;c(v2i-1)=1,1≤2i-1≤n;c(v2)i=2,2≤2i≤n.所有边均染颜色1.则每个顶点的扩展和计算如下:,3≤2i-1≤n-1;w(vn)=4.
显然w(v)i≠w(vi+1),vivi+1∈E(Fn)且1≤i≤n-1.下面考虑w(v0)≠w(v)i,1≤i≤n.由于 n≥4,可知,而w(v)i≤8,因此,w(v0)≠w(v)i,1≤i≤n.故当n为偶数时,c是Fn的一个NESD全2-染色。
综上可证 egndi∑(Fn)=2.
定理3设K1,(nn≥2)为n+1阶的星,则egndi∑(K1,n)=1.
给K1,n的顶点与边均染颜色1.则每个顶点的扩展和计算如下:w(v0)=2n,w(v)i=2,1≤i≤n.下面考虑w(v0)≠w(v)i,1≤i≤n.由于n≥2,可知w(v0)=2n≥4,而w(v)i=2,因此,w(v0)≠w(v)i,1≤i≤n.故c是K1,n的NESD全1-染色.
综上可证 egndi∑(K1,n)=1.
定理 4 设 S2n为 2(n+1)阶的双星,则 egndi∑(S2n)=2.
除顶点u0染颜色2外,其余顶点与边均染颜色1.则每个顶点的扩展和计算如下:w(u)0=2n+2;w(u)i=3,1≤i≤n;w(v)0=2n+3;w(v)j=2,1≤j≤n.
显然w(u0)≠w(v)0,下面考虑w(u0)≠w(u)i,1≤i≤n;w(v)0≠w(v)j,1≤j≤n.
假设w(u0)=w(u)i,1≤i≤n,有2n+2=3,即,与n为整数矛盾;假设w(v0)=w(v)j,1≤j≤n,有2n+3=2,即.与n为整数矛盾.因此,w(v)0≠w(u)i,1≤i≤n,w(v)0≠w(v)j,1≤j≤n.故c是S2n的NESD全2-染色.
综上可证 egndi∑(S2n)=2.
2 结束语
在文献[4]中探讨了路,圈,完全图,树等图的邻点扩展和可区别全染色,确定了它们的邻点扩展和可区别全色数.但没有给出轮,扇,星和双星的邻点扩展和可区别全色数.本文在路与圈的邻点扩展和可区别全染色的基础上,给出了轮,扇,星和双星的邻点扩展和可区别全染色,并确定了它们的邻点扩展和可区别全色数.另外,我们在之前也研究过两圈之联的邻点扩展和可区别全染色,并通过删边的方法得到了两路之联及路与圈的联图的邻点扩展和可区别全染色.那么,这种方法是否能够解决两轮之联,两扇之联及轮与扇的联图的邻点扩展和可区别全染色.这就是今后需要继续研究的课题.
