OFDM信号的新型自动识别与解调技术研究*
2018-12-19陈菊
陈 菊
(1.国防大学政治学院杨浦教学区学员三大队,上海 200433;2.解放军战略支援部队61486部队,上海 200072)
0 引 言
近年来,通信信号调制方式自动识别技术得到广泛深入的研究,在软件无线电、无线电频谱监测等方面得到越来越广泛的应用。过去人们对调制方式的自动识别研究大多针对FSK、PSK和QAM等单载波类型信号,而正交频分复用OFDM系统较一般的单载波通信系统能更充分利用频带,获得更高的数据传输速率,已经在许多通信领域(如欧洲数字音频广播DAB、数字视频广播DVB、ADSL、802.16WiMax)得到广泛应用。本文所讨论的问题是OFDM信号和单载波线性调制信号的区分以及OFDM信号调制规格的分析。文章第1节将简单介绍OFDM系统信号模型;第2节讨论OFDM信号特征的提取;第3节讨论OFDM调制规格分析技术;第4节讨论OFDM信号载频精确估计算法;第5节介绍实际应用效果;最后是结束语。
1 OFDM系统信号模型
OFDM系统基带信号模型[1]如图1所示。数据符号串并变换会使每个子载波上的数据符号周期(等于OFDM符号周期)相对地变长,而且使插入的保护间隔(即循环前缀)大于无线信道的最大时延扩展,这样可以减轻由无线信道的多径时延扩展所产生的时间弥散性对系统造成的影响,最大限度地消除由多径时延带来的符号间干扰。在这种情况下,信道可被认为是非频率选择性衰落信道,即平衰落信道。另一方面,数据符号周期的变长,会使得OFDM系统较普通的单载波通信系统对频率偏移更加敏感,从而使子信道之间的干扰大大增加,影响系统的性能。
设OFDM信号为:

这里,{cn,k}是符号序列,并假设是中心化、独立和同分布的;N为载波数;Δf是子载波间的频率间隔;g(t)为脉冲函数;P表示信号功率。另外,符号周期Ts=Tu+Tg,Tu称为有效符号周期,Tg称做保护间隔。

图1 OFDM系统信号模型
2 OFDM信号特征提取
2.1 四阶累量分析
观察式(1),根据中心极限定理,可知OFDM信号依概率收敛于高斯分布。为便于分析,这里把OFDM信号表示为:

其中:
现在讨论xr(t)在t0时刻的四阶累量:

由于各子载波符号间相互独立,应用四阶累量的多线性(multi-linearity)特性,四阶累量可写成:


由此,可得出下述结论:
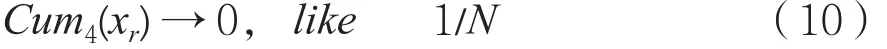
同理可得:

2.2 信号特征提取
根据文献[1],知道有些时间间隔的四阶累量表征调制的特征很显著;而其他时间间隔对四阶累量的值几乎没有影响。事实上,只需计算每个(0,η,η)时间间隔的四阶累量,η的取值为η∈[0,1.5Ts],四阶累量的计算公式为:

同理,可得:
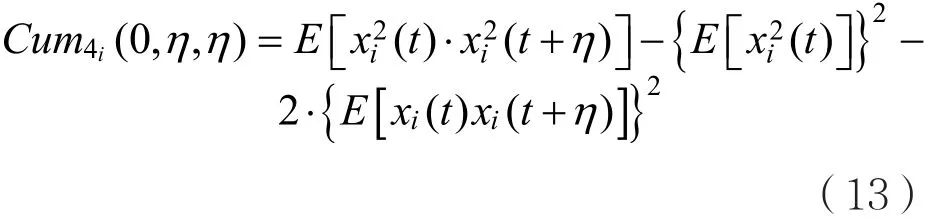
2.3 OFDM信号自动识别流程
基于信号四阶累量特征的OFDM信号自动识别流程如图2所示。

图2 OFDM信号自动识别流程
3 OFDM调制规格分析
OFDM调制规格分析的内容包括子载波间隔分析、各子载波频率计算、子载波数目(并行调制路数)计算、调制符号速率估计等。
3.1 子载波间隔自动测量算法
OFDM信号特征表征(如时域波形、频谱图等)包含有自身的特有信息,包括子载波间隔、子载波频率和子载波数目等。对一个OFDM信号(如图3所示,其中图3(a)中横轴为频率,纵轴为信噪比,图3(b)中横轴为时间,纵轴为幅度),要分析子载波间隔、各子载波频率以及子载波数目,传统的人工分析方法是使用降采样技术并结合频谱观测来实现。很显然,这种方法具有很大的局限性,尤其是当子载波数目较大时更是如此。为此,研究设计了一种基于自适应滤波和频谱变换技术的子载波间隔自动测量算法。算法原理如图4所示。

图3 某OFDM信号时域和频域

图4 OFDM子载波间隔自动测量算法原理
3.2 子载波频率和子载波数目自动测量算法
子载波频率和子载波数目自动测量均以子载波间隔参数信息为基础,通过自适应滤波和子载波间隔参数匹配,确定各子载波频率[2];通过自适应滤波和门限判决,确定子载波数目。图5是图3所示OFDM信号子载波频率测量的示意图(横轴为频率,纵轴为能量),清晰显示了各子载波频率所在位置和子载波间隔。在获得子载波频率位置和子载波间隔参数后,以信号原始频谱为基础,通过自适应滤波和门限判决,即可确定子载波数目。

图5 子载波频率测量
3.3 符号速率估计
3.3.1 频带边界虚音的定义
设OFDM信号最低音和最高音子载波频率分别为fmin和fmax,子载波间隔Δf,定义频带边界虚音(如图6所示)为[3]:


图6 频带边界虚音
3.3.2 基于频带边界虚音能量检测的符号速率估计算法
基于频带边界虚音能量检测的符号速率估计算法的基本原理:当所取信号序列位于同一码元内时,不包含有频带边界虚音fx1、fx2及其以外的信号分量;当所取信号序列跨在两个码元之间时,这段信号序列中会包含有频率fx1、fx2的信号分量。因此,将OFDM信号首先进行频带边界虚音fx1(或fx2)信号滤波、零中频变换,按滑动窗计算窗口内信号能量,根据窗口能量的变化规律,获取码元转换点信息,进而求取符号速率(如图7所示)。
这里需要注意,滑动窗宽度W的选择必须满足:

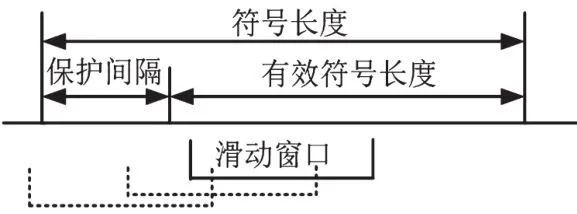
图7 滑动窗信号能量计算
图8 是一个典型的频带边界虚音窗口能量分布图(横轴为频率,纵轴为能量)。信号来源是某方向短波36路OFDM突发通信信号。图9是由频带边界虚音窗口能量分布求得的符号速率示意图(横轴为频率,纵轴为幅度),显示符号速率为49.8 Baud,实际信号的符号速率50 Baud。需要说明的是,这里符号速率计算精度与观测信号长度密切相关。

图8 典型的频带边界虚音窗口能量分布

图9 基于频带边界虚音窗口能量分布的符号速率估计
4 OFDM信号解调关键技术
OFDM信号解调涉及载频精确估计、定时同步提取等多个环节。对于短波突发信号,还涉及信号检测、调制识别等诸多问题。这里仅讨论载频精确估计算法。
4.1 子载波间干扰和频偏关系
当OFDM系统中存在频率偏移时,经模数转换后的接收信号可表示为:

其中,第k个子载波上的数据为:

由:

其中,第一项为有用信号,第二项为其他载波信号的干扰,即ICI,最后一项为高斯白噪声解调的结果。考虑到数据符号均值为零,互不干扰,则信干比为:

4.2 基于迭代运算的载波频率精确估计算法
理论分析和实际经验表明,OFDM信号解调时对子载波频率估计精度有很高的要求[4]。为此,研究设计了基于迭代运算的载波频率精确估计算法。算法的基本原理是,以子载波频率估计值(或标称值)为中心频率点,设定一个置信频率区间,根据设定的搜索步长划分置信频率区间,然后分别计算置信频率区间的各划分频点,搜索出最佳频点。图10是一个典型的载波频率(频偏)精确估计结果示意图,图中搜索步长0.02 Hz。

图10 一个典型的载波频率(频偏)精确估计结果
5 实际应用效果
前述OFDM信号自动识别、子载波间隔、频率与数目自动测量、信号符号速率估计算法和载波频率精确估计算法已在实际工作中得到了充分应用。短波信号测试库样本包括MFSK、GMSK、MPSK、MQAM及OFDM等类型,其中OFDM类型包括16路、18路、20路、36路、39路多种OFDM信号。对于自建的近100个实际信号的短波样本库,OFDM信号识别率大于75%;OFDM子载波频率间隔和子载波频率测量误差不超过10%;子载波路数测量误差不超过5%。以上指标可以满足实际工作的要求。
6 结 语
本文在对OFDM信号特性进行分析的基础上,对其四阶累量进行了详细分析和讨论,设计了用于OFDM信号识别的四阶累量特征提取方法,研究和讨论了OFDM子载波间隔、频率以及数目自动测量等调制规格分析技术。实际应用结果表明,本文讨论的OFDM信号自动识别与调制规格分析技术具有有效性。
