基于DTW的坦克换挡动作时间序列匹配方法

魏子剑，张进秋，刘义乐

（陆军装甲兵学院，北京 100072）

0 引言

我军坦克驾驶训练由于缺少数字化记录手段和相应分析方法，一直停留在经验教学阶段，教员只能根据车辆运动状态通过主观打分来评价乘员的训练效果。如何采用数字化方法对乘员驾驶技能进行评价，以此提高训练效率和质量成为当前驾驶训练研究的重要内容。石志涛[1]等通过对传感器进行选型和对驾驶动作记录仪进行设计，搭建了驾驶操作数据采集系统，采集的操纵件状态信息再现了乘员的驾驶动作，实现了驾驶操作的数字化记录；刘义乐[2]等提出借助位移传感器用操纵件位移数据记录乘员动作，同时提出以给定的驾驶规则时序识别换挡动作的方法，有效地识别出了换挡动作。本文在两人研究的基础上，借助数据采集系统采集乘员的换挡动作时间序列，对时序数据进行处理得到单个换挡动作的序列，将这些单个序列和标准的换挡动作序列进行动态弯曲距离度量，实现了对换挡动作时间序列的数字化匹配。

1 动态弯曲距离

时间序列的相似性度量即衡量两组时间序列的相似程度，是时间序列数据挖掘的核心问题之一[3-4]。时间序列的相似性度量一般指的是序列之间的距离度量，两个序列之间距离越小则相似度越高。动态弯曲距离（DTW）是常见的距离度量方法之一，不要求序列按照时间轴进行点对点计算。由于乘员的换挡动作时间不同，序列长度也不尽相同，因此，动态弯曲距离适用于换挡动作时间序列的距离度量。

设有长度分别为m和n的时间序列A和B：

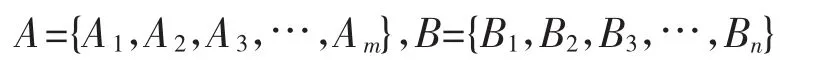
构造一个 m×n 的矩阵，其中第（i，j）个元素是A、B序列中点Ai和Bj的距离，记作dij。根据欧氏距离计算方法，dij=（Ai-Bj）2。如图1所示，一条弯曲路径w是由上述矩阵所有元素构成的连续路径，这条路径实质上是时间序列A和B之间的一个映射，W的第k个元素的坐标被定义为Wk=（i-j）k，可得到一个路径集 W={w1，w2，w3，…wk|max（m，n）≤k＜m+n-1}。

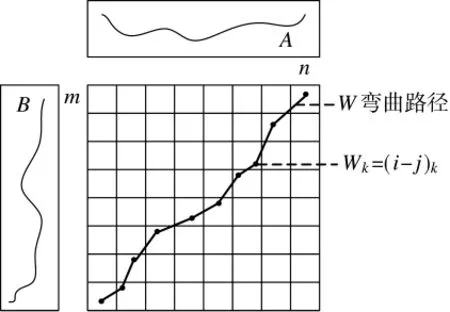
图1 弯曲路径示意图

该路径满足以下条件限制[5]：

1）边界条件：W1=（1，1）且Wk=（m，n），即要求弯曲路径必须从矩阵的起始位置处开始和对角的结束位置处结束；

2）连续性：给定Wk=（a，b）和Wk-1=（ak-1，bk-1），要求a-ak-1≤1且b-bk-1≤1，即要求弯曲路径每一步的设定都是连续的；

3）连续性：给定Wk=（a，b）和Wk-1=（ak-1，bk-1），要求a-ak-1≥0且b-bk-1≥0，即要求路径必须在时间轴上是单调的，也就是说路径通过点（i，j）同时必须至少通过点（i-1，j-1），（i-1，j）或（i，j-1）中的一个。满足上述条件的路径有很多条，可计算每条路径到达点（m，n）时总的累积距离，选择具有最小累积距离者为最佳路径，即：

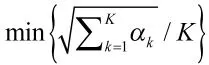
式中：αk为路径w通过第k个元素（i，j）k时2个时间序列对应点Ai和Bj之间的距离dij；K为路径w的长度，用于消除不同弯曲路径长度的影响。基于动态最优化原理可知，设点（i，j）在最佳路径上，那么从点（1，1）到点（i，j）的子路径也是局部最优解，也就是说从点（1，1）到点（m，n）的最优路径可以由时间起始点（1，1）到终点（m，n）之间的局部最优解通过递推搜索获得。构造累积距离矩阵，点（i，j）计算公式为：

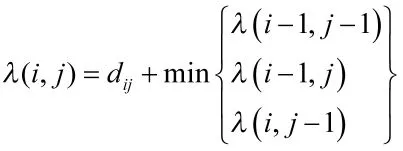
2 换挡动作时间序列匹配

2.1 数据预处理

在加速踏板和离合器踏板的踏板位置上布设位移传感器，变速杆排挡位置上布设光电开关传感器，借助采集仪采集3个操纵件的状态信息。采集得到的变速杆数据 -1、0、1、2、3、4、5 分别表示倒挡、空挡、一挡、二挡、三挡、四挡、五挡，加速踏板和离合器踏板位移数据为十进制。借助MATLAB编程，对加速踏板和离合器踏板数据进行预处理得到0、1矩阵。经过数据预处理的序列可以大大缩减距离度量时间和复杂度。

为消除驾驶过程中车辆振动和仪器误差对采集数据的影响，需要对加速踏板和离合器踏板数据进行阈值处理。将时序第i+1行数据和第i行数据做差，得到差值b，对差值b设定一个阈值4 mm。当差值|b|＜5，认为相邻两行数据未发生变化，即操纵件位移和状态未发生变化，此时对第i+1行数据赋值为0。当差值|b|≥5时，认为操纵件位移和状态发生变化，有动作产生，此时对第i+1行数据赋值为1。经过阈值处理得到矩阵H1。

对矩阵H1中加速踏板和离合器数据分别进行差值处理，即将时序第j+1行与第j行数据做差，对差值取绝对值并赋值给第j行。经过差值处理得到矩阵H2。数据预处理算法如下：

2.2 建立标准序列模型

以一挡换二挡为例，助教在实车上做10次换挡动作，对采集的10次换挡动作序列数据按照上述程序进行数据处理，得到10次换挡动作的单个序列。对10个序列进行编号，两两之间进行动态弯曲距离度量，每个序列与其他9个序列的距离之和最小的作为一挡换二挡的标准序列。

动态弯曲距离度量的算法如下：

10个序列经过上述算法进行距离度量后，相互之间的动态弯曲距离如下页表1所示。

由表1可以看出助教的第2次换挡动作序列与其他9个序列距离之和最小为10.629，将第2次换挡动作序列作为标准的一挡升二挡动作序列。

2.3 序列匹配

在对20名学员进行换挡动作考核中，每名学员做2次一挡升二挡动作，助教对每名学员每次换挡动作进行打分。同时借助采集仪对每次换挡动作序列数据进行采集记录，在MATLAB上进行数据预处理并与标准序列进行动态弯曲距离度量。序列距离和助教打分之间的映射如下页表2所示。

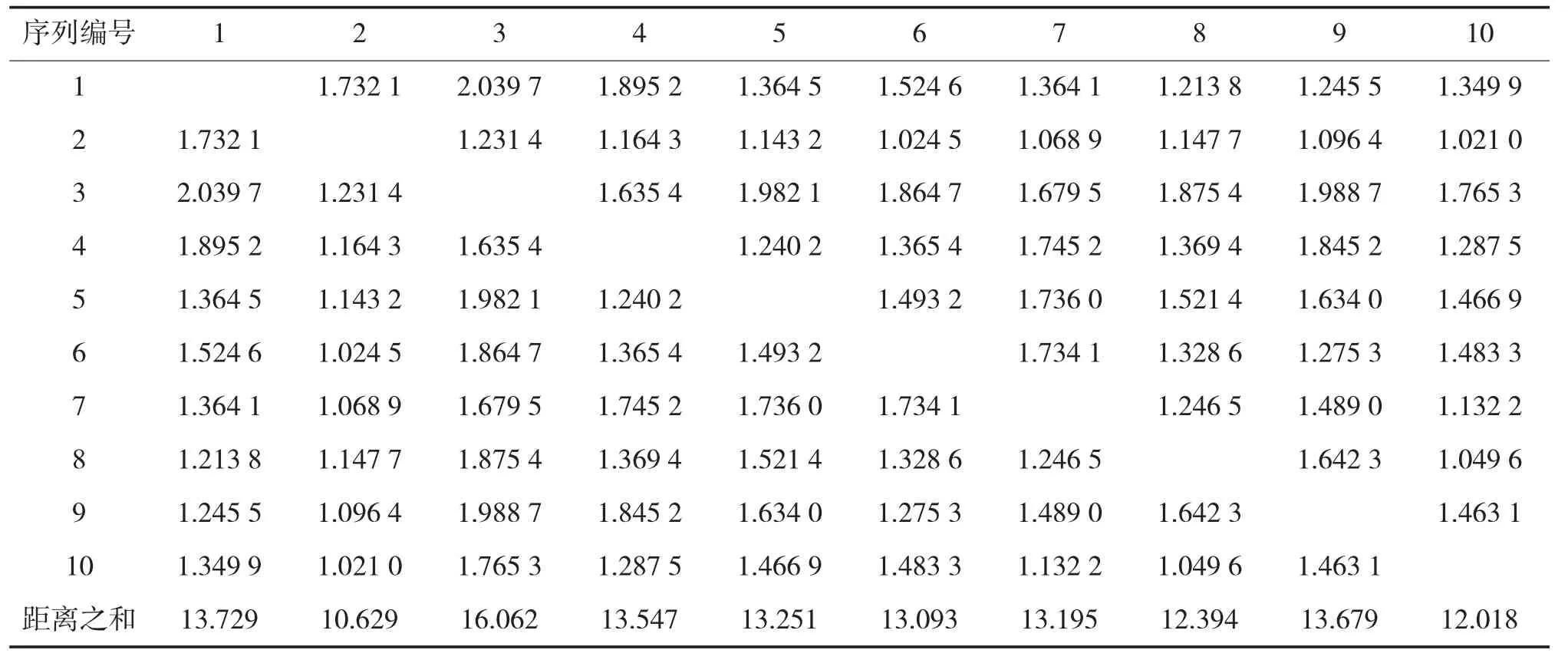
表1 10个换挡动作序列动态弯曲距离表

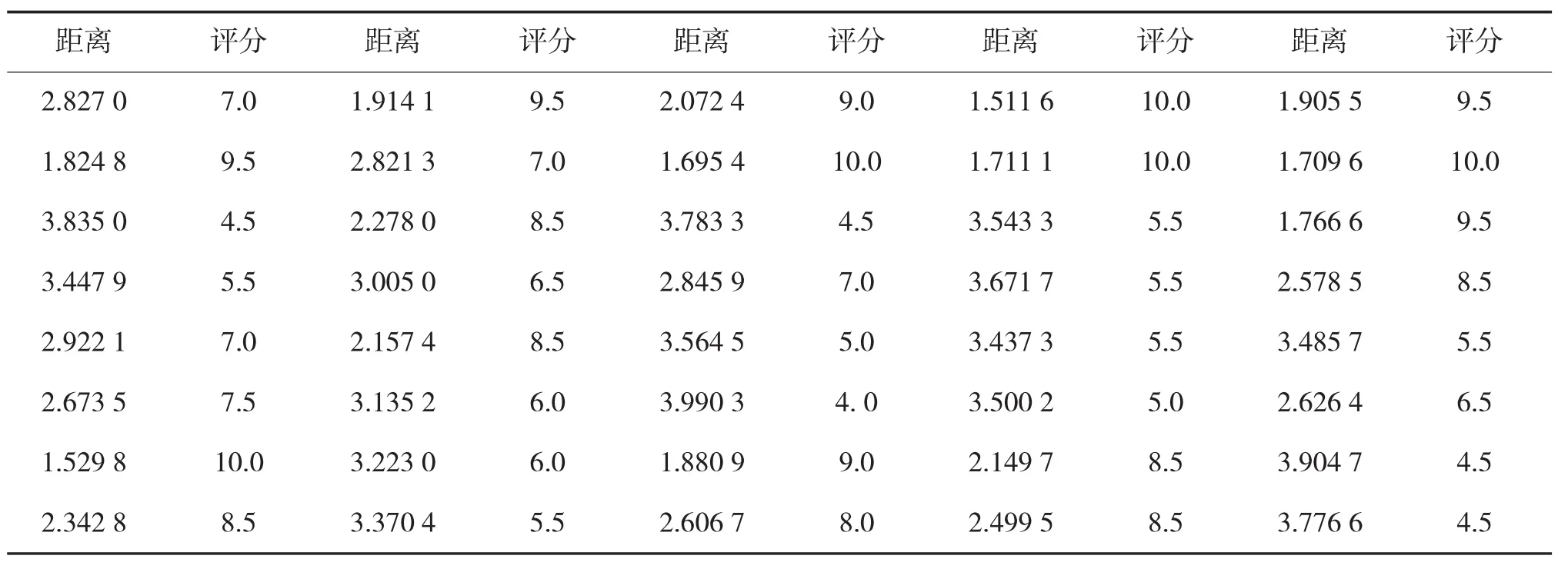
表2 序列距离与助教打分对应表

助教打分作为助教主观对乘员驾驶动作的评价，一般分为3个等级：优秀、良好和不及格，对应的分数段分别为：8.5～10.0（包括 8.5）、6.0～8.5（包括6.0）和0～6.0。按照3个评价等级对序列距离进行统计，如表3所示：

表3 序列距离与评价等级统计表

3 结论

在当前对乘员的驾驶技能进行评价时仍采用助教打分的方式，难以客观全面地评价乘员的驾驶水平。为解决这一问题本文以换挡动作一挡升二挡为例，通过建立换挡动作的标准序列模型，将乘员的换挡动作序列与标准序列进行动态弯曲距离度量，并把度量距离与助教打分进行映射，形成了换挡动作序列距离库，初步实现了对乘员驾驶动作的客观数字化评价。将序列距离库的范围扩大，并将以动态弯曲距离度量为基础的匹配方法应用在复杂的驾驶科目是下一步研究的重点内容。