基于时间-距离像的弹道目标进动特征提取*

韩 睿，耿志远

（1.淮安信息职业技术学院计算机与通信工程学院，江苏 淮安 223003；2.空军工程大学航空航天学院，西安 710038）

0 引言

弹道导弹防御是国防建设的重要组成部分，其中中段防御被认为是反导的关键阶段[1]。在中段，弹道目标为保持自身稳定，除了平动外，还存在旋转、翻滚、进动、章动等不同形式的微动[2]。本文主要对锥柱体目标进行研究。文献[3]利用SSM算法提取了散射中心的位置信息，根据散射中心位置与目标参数之间的关系求解出了目标进动参数和结构参数。但由于单一雷达视角的局限性，该文通过设定修正因子来提高参数的求取精度，算法比较复杂。文献[4-5]通过确定时间-距离像分布与散射中心的位置关系，实现了进动参数和结构参数的联合提取并对影响参数精度的因素进行了仿真分析。文献[6]利用雷达双视角距离像的信息，研究了雷达部署在空间目标落体方向上时锥体目标参数的求取，仿真分析了半锥角的估计与信噪比的关系。

基于宽带雷达距离分辨率高，能够获得目标精细的结构参数，本文利用两部宽带雷达获取的时间-距离像，对锥柱体目标4个散射点可见的情况进行了研究。针对锥柱体散射点数量较多的情况，根据定义的粗匹配模块、精匹配模块和散射点类型识别来联合两部雷达获得的相同散射点的微动信息，并根据两部雷达微动信息实现了进动参数和结构参数的求解。仿真验证了本文方法的有效性和实用性。

1 微动建模

1.1 锥柱体进动建模

图1 弹头进动模型示意图

以锥柱体对称轴与进动轴的交点作为坐标原点O，建立坐标系O-xyz，如图1所示。以进动轴为z轴，定义初始时刻对称轴与z轴所在平面为yOz平面，x轴方向符合右手螺旋准则。设第i部雷达视线的俯仰角为αi（i=1，2），方位角φi，进动角为θ，进动角速度为ωc，半锥角为ε，锥体高度为h1，锥体底面半径为r，锥体底面圆心O'到O点的距离为h2，柱体下底面中心O''与O点的距离为h3。雷达视线方向与对称轴构成的平面为底面圆环的电磁波入射平面，该平面与锥体底面交于B、C两点，与柱体下底面交与D、E两点。雷达视线在O-xyz中的俯仰角和方位角为，与锥柱对称轴的夹角为β（雷达视角）。初始时刻雷达到坐标原点O的距离为R0且满足远场条件。

在光学区，对于锥柱体旋转对称目标，其高频散射特性主要由锥顶散射点、锥体底面边缘两个散射点和锥柱体下底面边缘两个散射点确定[3]。当雷达视角满足时，有4个散射点可见，分别为散射点A、C、D、E。经过几何推导可得雷达视线角β满足：

则散射中心与雷达之间的距离表达式近似为：

1.2 距离像分析

结合式（1）和式（2）可以看出，散射点投影长度变化比较复杂，直接进行特征提取较为困难，需要对式（2）进行合适的变形。为了简化表达式，现将散射点 A、C、D、E 命名为散射点 1、2、3、4。散射点长度表达式可表示为：

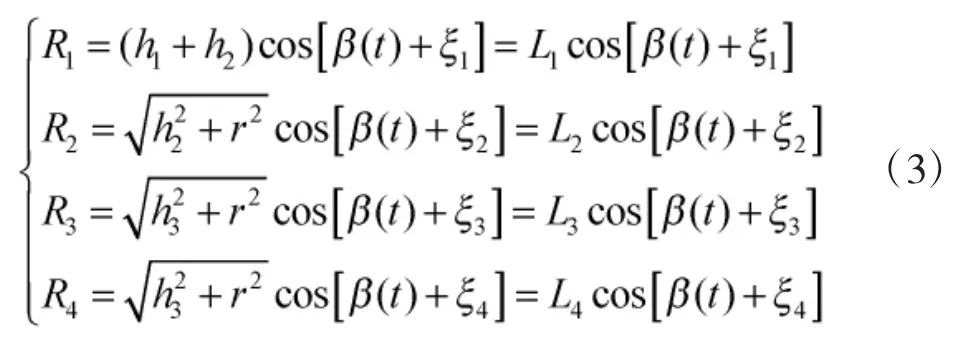
由式（1）可知，雷达视线角 β（t）的变化周期与进动周期ωc有关，而变化的范围由θ和αi确定。由于进动角 θ很小[8]，一般在 5°～15°范围内，可以利用这一信息对散射点的投影长度进行近似：

上式表明，锥柱体散射点在雷达视线上的投影长度变化可近似为正弦变化，分别为正弦曲线的中值、幅值、角速度和初相，可利用合适的曲线提取算法进行获取，其中，φi为已知雷达方位角、ξj与锥柱体的结构参数有关。

2 散射点匹配关联

由于雷达视角的不同，观测相同散射点获得的距离像序列存在差异，且部分散射点会出现交叉的情况，为了准确利用每部雷达的散射点微动信息，需要先对散射点进行匹配关联。然后利用相同散射点在不同雷达视角下的观测信息进行特征分析和参数提取。匹配过程主要包含如下3个部分。

2.1 曲线参数提取

本文采用广义Hough变换[7]提取式（5）中的曲线参数。广义Hough变换能够检测满足特定解析式的各类曲线，精确获得曲线的参数，且具有一定的抗噪性能。考虑到广义Hough变换的运算量是随着参数空间维数的增加而成指数增加。因此，在进行广义Hough变换之前需要对部分参数进行提取。进动角速度ω的提取与其他参数相比相对容易，采用文献[9]提出的将自相关法与平均幅度差函数法相结合的方法来提取进动角速度ωc。由式（5）可以看出，散射点在雷达视线上的投影长度可近似为正弦，参照文献[7]的方法，采用广义Hough变换对参数进行提取。广义Hough变换的基本思想是将图像测量空间的一点变换到参数空间中的一条曲线或一个面，而具有同一参数特征的点变换后在参数空间中相交。通过判断交点处的积累程度来完成特征曲线的检测。

2.2 粗匹配模块

粗匹配的思想是：以雷达1中某个散射点的距离像曲线信息为匹配样本，将雷达2中每个散射点距离像的信息与雷达1中的匹配样本进行匹配，求解出满足设定门限的散射点。此时，雷达2中满足门限的散射点可能不止一个，这就需要下一步的精匹配进行精确筛选。考虑到研究的锥柱体散射点较多，两部雷达提取的散射点信息进行两两组合的情况较多。如果直接对两部雷达获取的散射点距离像进行精匹配，会占用过多的资源。根据式（5）求出散射点距离像的幅值和中值，定义相应的函数进行粗匹配，表达式如下：

其中，l1jA和l1jC为雷达1获得的散射点j的幅值和中值，l2kA和l2kC为雷达2获得的散射点k的幅值和中值。aA和aC分别为幅值一致性和中值一致性，满足aA+aC=1。通过仿真实验，发现不同的散射点对应的中值差别较大，可将aC适当取大一些。所以加权系数可按照aC≥aA进行设定。满足的散射点进入下一步的精匹配模块，其中η为相应的选择门限。在门限选取为0.2时，可以保证在信噪比为5以上时，两关联的两条曲线拟合趋势接近。

2.3 精匹配模块

精匹配的思想是：提取满足粗匹配门限散射点t时刻的位置和幅度信息与样本散射点t时刻的位置和幅度信息进行匹配度检测。当满足粗匹配门限的散射点不是唯一时，多次取散射点不同时刻的位置和幅度进行检测，直到满足存在一个散射点与样本散射点匹配的条件。设雷达1观测下散射点j的位置和幅度信息为p1j和q1j，雷达2观测下散射点k的位置和幅度信息为p2k和q2k，其中位置和幅度信息可通过散射点的距离像序列获得，定义精匹配公式为：

其中，δp与δq分别表示位置与幅度变化的方差，仿真实验表明，δp设为距离像的分辨率，δq一般设为2到5之间的效果较好；b1与b2分别表示位置一致性与幅度一致性的加权系数，满足b1+b2=1。幅度变化的连续性与等效散射中心对应结构有关，可将b1取得大一些。当p1j=p2k，q1j=q2k时，两个散射点完全吻合，匹配度为1。

在对雷达1和雷达2散射点进行匹配时，应使得整体匹配单元最大。其中匹配度最大的两个散射点视为关联的两个散射点，同时将关联的散射点从匹配单元中去除。再重新设定位置和幅度的加权系数，进行下一轮的匹配，直到剩余匹配度最大值小于某一门限或者所有散射点均得到匹配，此时即完成了对散射点的匹配。此时，门限选取为0.05，在保证匹配一致的情况下，对关联的两条曲线进行高质量的拟合逼近，实现曲线的精确匹配。

2.4 散射点类型识别

在对散射点匹配关联的基础上，要准确提取锥柱体的结构参数，还需要对匹配关联后的散射点进行类型识别。由式（3）可知，每个散射点的初相差ξj均不同且仅与锥柱体的结构参数有关，可利用其进行散射点类型识别。利用已知的雷达方位角补偿提取得到的曲线参数初相，可以得到初相差ξj。由式（2）和式（3）可知散射点 A 的初相差 ξ1=0，散射点 C、E 的初相差 ξ2、，散射点D的初相差。同时散射点D、E的初相差还满足关系式ξ3+ξ4=0。通过获取散射点初相差的信息，即可实现对散射点类型的识别。

3 微动参数求解

3.1 进动角θ提取

由式（5）可知，散射点时间-距离像的幅值和中值存在进动角θ与雷达视线的俯仰角αi的耦合，单部雷达难以估计，需要利用两部以上雷达的观测信息进行求解。在组网雷达体系中两部雷达1和2的观测条件下，利用广义Hough变换可得到散射点的信息矩阵，其中 j=1、2、3、4。利用信息矩阵A可得到进动角θ矩阵为：

上式表明每个散射点的微动信息均可求解出进动角，对所有求出的进动角进行加权平均得到最后的进动角θ。

3.2 结构参数的求解

在两部雷达1和2的观测条件下，利用广义Hough变换提取出的参数，求出各个散射点的Lj为：

进一步可求出雷达视角α1、α2为：

在2.4节识别出散射点类型的基础上，在同一位置（同一时刻），确定出散射点D、E的投影长度，并求出散射点D、E投影长度之差的绝对值如下：

由式（9）～式（12）可以看出，锥柱体的结构参数和雷达视线角均与进动角有关，进动角的精确度决定了整体参数提取的精确度，说明了对进动角进行数据融合来提高精度是十分必要的。综上所述，基于两站时间-距离像的弹道目标进动特征提取的具体步骤如下：

步骤1建立两站宽带雷达模型和锥柱体进动模型，并对散射点在雷达视线方向上的投影长度进行分析。对两部雷达接收的回波信号提取各散射点时间-距离像曲线。

步骤2利用广义Hough变换将散射点的时间-距离像上的任意一点映射到三维空间参数空间中并通过峰值搜索求出参数。

步骤3根据不同的散射点中值ljC和ljA幅值的不同，定义粗匹配公式对散射点进行粗匹配；然后根据散射点每一时刻的位置和幅度信息，定义精匹配公式对满足粗匹配的散射点进行精匹配；最后根据散射点初相差仅与结构参数有关这一信息，进行散射点类型识别。

步骤4联立两部雷达同一散射点提取的曲线参数求解出进动角θ。由于每个散射点求解出的进动角不同，为了得到精确的进动角，以进动角的均方误差进行加权系数的求解，将不同的进动角进行融合。用融合后的进动角对锥柱体的结构参数和雷达视角进行求解。

4 仿真实验

仿真参数设置：假设目标为旋转对称锥柱体，目标参数设置为：h1=1.5 m，h2=1 m，h3=2 m，r=0.5 m，θ=10°，锥旋角速度 ωc=4π rad/s。目标散射系数均为1 m2。雷达参数设置为：载频f=10 GHz，信号带宽为4 GHz，雷达脉冲重复频率为1 000 Hz，观测时间1 s，预处理后信噪比为10 dB。

图2 雷达1获得的时间-距离像序列

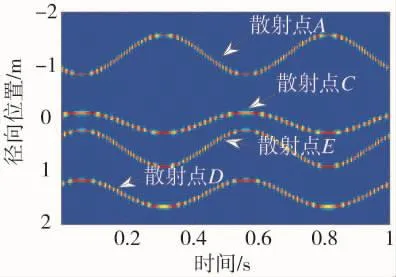
图3 雷达2获得的时间-距离像序列

图4 散射中心及其关联结果

图2和图3为两部雷达获得的时间-距离像序列，其中第1部雷达视线与锥转轴的夹角α1=100°、方位角为 φ1=45°，第 2 部雷达视线与锥旋轴的夹角α2=120°、方位角为φ2=60°。采用广义Hough变换对图2和图3中散射点的时间-距离像进行参数求解，根据第4节散射点匹配的方法确定出散射点的类型，再由式（8）估计得到每个散射点进动角的值。由表1可以看出，散射点A求得的进动角误差较小，散射点C、D、E由于式（4）的近似，误差比散射点A大。利用表1数据平均后的进动角θ代入到式（9）～式（12）可分别解出锥柱体结构参数和雷达的视角，得到表2的数据。

5 结论

本文对锥柱体弹道目标在多散射点的情况下进动参数如何提取进行了研究。利用两部雷达的观测信息对目标参数进行了提取。仿真结果表明：

表1 进动角估计结果

表2 进动和结构参数估计结果

1）利用两部雷达获取的微动多视角信息即可提取出弹道目标进动参数和结构参数。

2）可通过不同散射点具有不同的微动信息定义出散射点匹配门限来区分多散射点情况。

3）本文方法适用于多散射点目标的特征参数提取，为了弹道群目标的分辨提供了一个参数提取方法。下一步工作将对多目标多散射点的参数提取进行研究。