透过散射介质对直线运动目标的全光成像及追踪技术
2018-12-18贾辉罗秀娟张羽兰富洋刘辉陈明徕
贾辉 罗秀娟 张羽兰富洋 刘辉 陈明徕
1)(中国科学院西安光学精密机械研究所,西安 710119)
2)(中国科学院大学,北京 100049)
(2018年5月14日收到;2018年9月12日收到修改稿)
1 引 言
散射介质固有的非均匀性导致光透过介质后形成一个复杂的散斑,影响了光学成像系统的成像分辨率和穿透深度.透过散射介质的全光场成像受到越来越多研究人员的关注,其在生物医学、安防和许多工程领域具有重要的应用价值.例如:对生物组织内部病变细胞的医学成像以及透过云、雾、霾、雨、雪、浓烟等散射介质的成像或遥感测绘等.近年来,研究人员利用记忆效应[1−5]、相位共轭[6−8]、传输矩阵测量[9−12]等技术对透过散射介质的成像进行了研究,取得了一些重大进展.然而,这些技术通常要求散射介质和(或)目标处于静止状态,轻微的运动就会使成像质量严重退化.本文基于散射介质的光学记忆效应理论[13]并结合散斑相关[1,14]的方法,采用散斑差值自相关实现了透过散射介质对运动目标的高分辨率全光成像;提出了一种采用散斑差值自相关对运动目标进行实时追踪的技术,成像过程中使用赝热光照明目标.近期,Cua等[15]实现了采用空间光调制器对明视场中的运动目标成像.本文在赝热光的产生方式中,没有使用价格昂贵的空间光调制器,而是使用旋转硫酸纸改变激光的相关性,使用方便且节约了成本.此外,基于手机相机拍摄散斑图的思路,为研发应用于低成本的便携式设备提供了参考.
2 基本原理
2.1 散斑相关
光束透过散射介质,出射光斑形成一个无规则的散斑,当入射光束偏转一个小角度δθ时,偏转前后两幅散斑的相关度[13,16]表示为
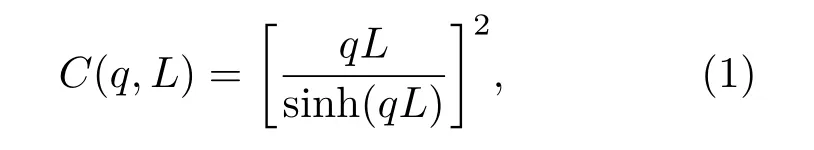
L是散射介质的有效厚度,q=2πδθ/λ,λ为波长,δθ为光束入射角.根据散斑相关函数C(q,L):δθ在一定范围内时,即光束入射角在一定范围内时,C值接近1,也就是出射散斑场近乎相同,散斑只是发生了一定的平移,平移量和入射角度有关,该现象称之为光学记忆效应.
根据光学记忆效应理论,散射成像的过程是点扩散函数(系统的响应函数)与物体的卷积过程.若目标被窄带宽非相干光照明,构成强度的线性平移不变系统[2],如图1(a)所示,目标信息经过散射介质散射,根据光学系统的卷积定理,经过散射介质出射的散斑光强可表示为
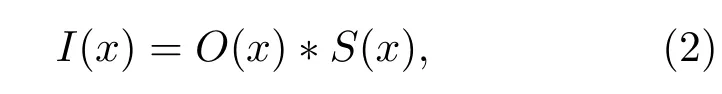
其中,∗代表卷积运算,S(x)代表系统的光强扩散函数(PSF),I(x)和O(x)分别代表探测到的散斑光强和目标强度,x代表目标所处的位置.图1(b)为经过散射介质出射的散斑光强图,由(2)式可知,该图像为携带目标信息的散斑图.做散斑光强的自相关:
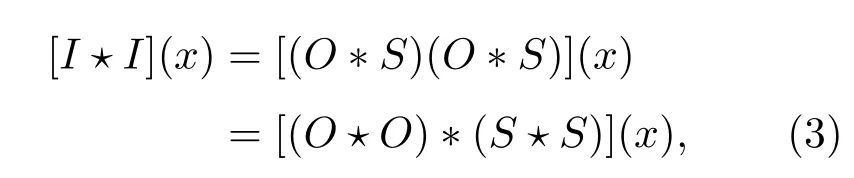
其中,⋆代表相关运算,S⋆S近似为窄脉冲[1,17].也即光强自相关近似为目标物体的自相关[I⋆I](θ)≈[O ⋆ O](θ),如图1(c)和图1(d)所示.
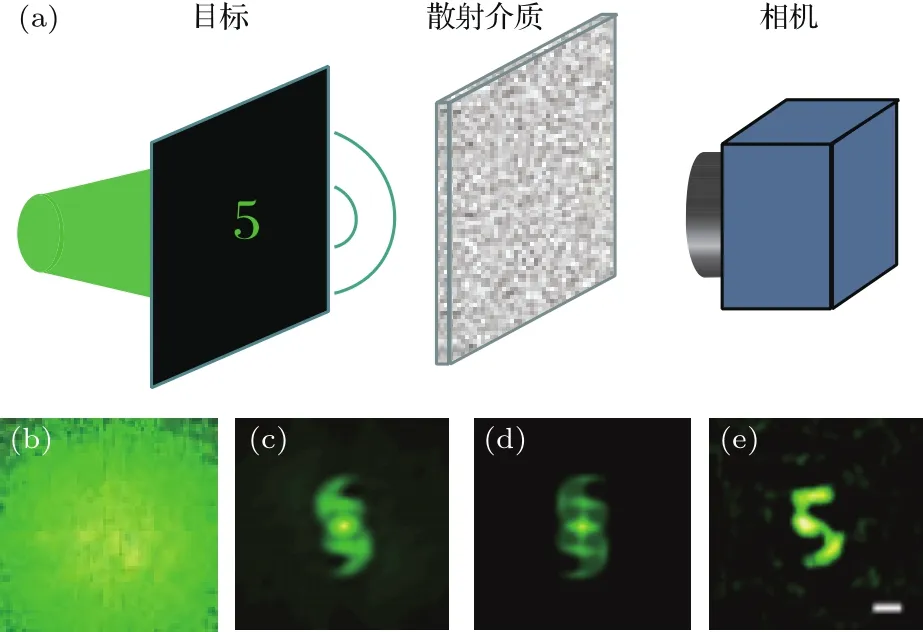
图1 透过散射介质的散斑相关成像 (a)原理示意图;(b)散斑光强图;(c)散斑光强的自相关图;(d)原始目标的自相关图;(e)重建目标图像Fig.1.Imaging through scattering layers by speckle correlations:(a)Diagram of the principle;(b)raw camera image;(c)the autocorrelation of the raw camera image;(d)the autocorrelation of the original object;(e)reconstructed object.
由自相关定理,函数的自相关与其能谱密度构成傅里叶变换对:

其中FT{}代表傅里叶变换运算,由此得到目标傅里叶频谱的振幅信息,由傅里叶光学理论可知,得到目标频谱的相位信息,即可实现目标的高分辨重建.利用Fienup等[18,19]的相位恢复算法,做如下四步迭代:
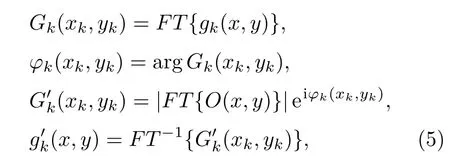
迭代初始值g1(x,y)任意赋值,gk(x,y)为第k次迭代,FT−1{}代表傅里叶逆变换运算,第k+1次迭代由第k次迭代结果得到,在此过程中对目标图像进行物理约束,可以使用约束条件“误差减小法”和“混合输入-输出法”.“误差减小法”的约束条件为
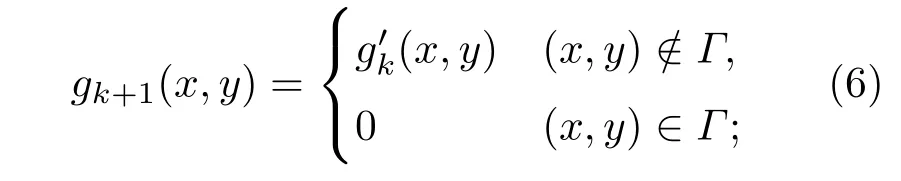
“混合输入-输出法”的约束条件为
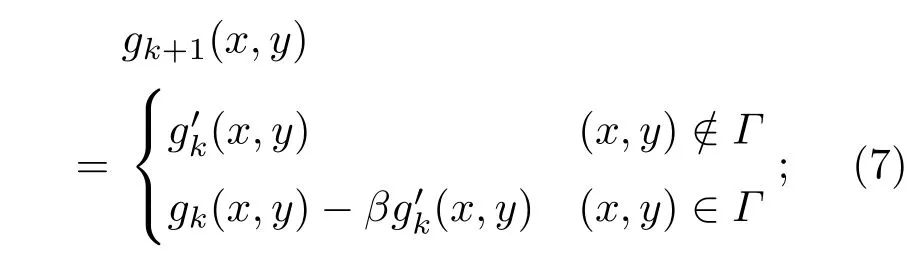
2.2 散斑差值自相关
当隐藏在散射介质后的目标在激光束横截面内运动时,光学系统仍旧是强度的线性系统,但由于目标的运动,造成散斑颗粒的模糊,使得背景噪声增大,从散斑背景中提取出目标的信息[15,20],根据光学系统的卷积定理,将(2)式改写为
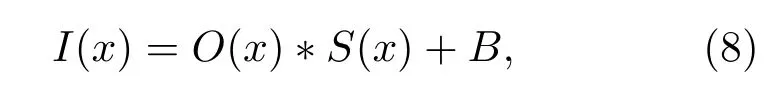
其中,B表示由于目标运动产生的散斑背景噪声.目标移动∆x距离,相机接收的散斑光强为
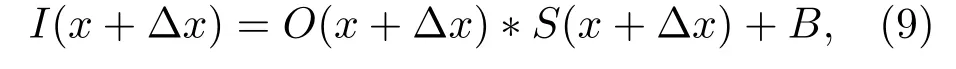
将两帧散斑相减,从散斑差值中提取目标信息,
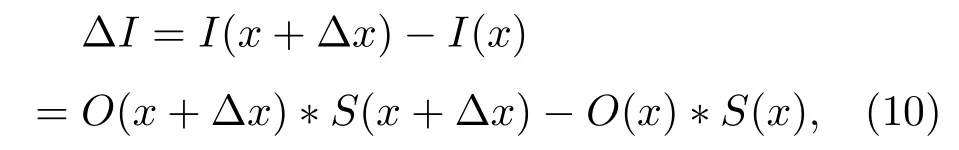
然后对散斑差值做自相关:

当采集的两帧散斑在一个记忆效应角范围内时,S(x)和S(x+∆x)近似相同,统一表示为S,将(11)式改写为
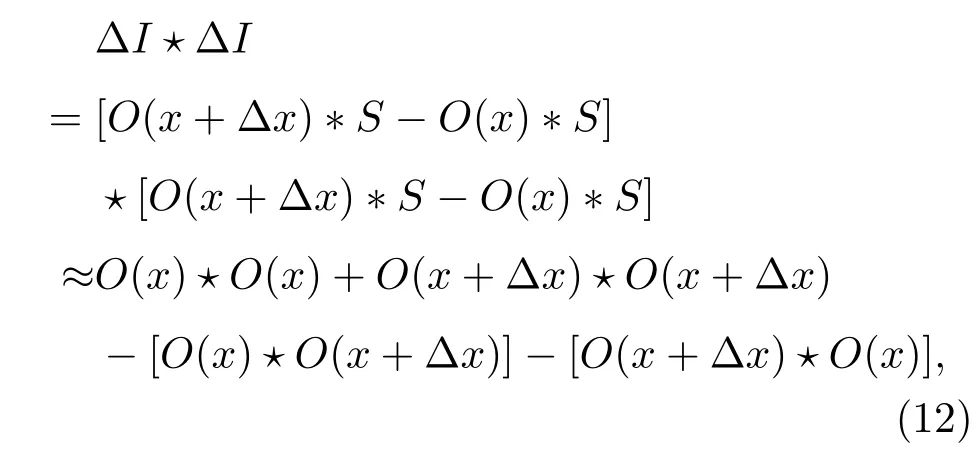
上式包含四项相关,其中前两项为目标自相关,位于输出平面中心,提取目标自相关信息,利用(4)式和Fienup相位恢复算法对目标进行重建.根据成像系统放大率β=u0/u=y0/y,其中,u0是相机到毛玻璃的距离,u是目标到毛玻璃的距离,y0为系统最终重建出的目标大小,y为目标实际大小.在该成像系统中,重建目标大小可表示为
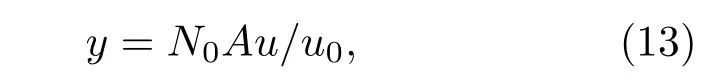
其中,y0=N0×A,N0为重建出的目标所占的像素数,A为像元尺寸.(12)式后两项为目标移动前后的互相关,其中心分别位于目标自相关左右两侧∆x处,∆x=∆P×A,∆P为自相关和互相关之间偏移的像素数.同理,当目标运动时,在一个记忆效应角度范围内,根据散斑差值自相关图中偏移的像素值,可计算出目标实际移动的距离为
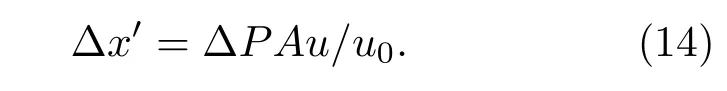
随着目标的运动,互相关信息将出现在散斑差值自相关图的不同位置,根据互相关的位置可对目标进行追踪.
当目标运动范围较广,采集的两帧散斑在一个记忆效应角度范围外时,S(x)和S(x+∆x)不具有相关性,S(x)⋆S(x+∆x)形成了一个弥散斑,如(11)式所示,噪声加在了两侧的互相关中,导致散斑差值自相关图中背景项增大.但这并不影响目标运动范围,不论目标在任何位置,(11)式中目标自相关信息不变,均可成像;对于目标追踪,目标的运动方向和距离是相对的,只要采集的相邻两帧散斑在一个记忆效应角度范围内,均可利用(12)式做出目标的散斑差值自相关图,从而求出目标相对运动距离.总之,采集的相邻两帧散斑需在同一个记忆效应角内,只有这样,才能保证运动距离的计算精确度.其中,探测器的视场角及探测器前的小孔限制了系统的视场角,因此限制了目标运动范围,赝热光源的大小同样也限制目标运动范围.
3 实验验证方法及结果
本文对隐藏在散射介质后的目标进行了两组成像实验,来对比验证采用散斑差值自相关的方法对运动目标的成像能力.并给出了目标运动距离的计算公式,实现对运动目标的实时跟踪.实验中采用波长532 nm的Nd:YAG固体激光器,扩束为直径2.5 cm的光束照射旋转硫酸纸产生赝热光照明目标.实验中对透射式目标进行成像,采用毛玻璃作为散射介质,并用手机相机(荣耀9)拍摄散斑图.
3.1 静止目标成像
第一组实验是对隐藏在散射介质后的静止目标成像,实验装置如图2所示.经过扩束的激光光束照射旋转硫酸纸产生赝热光照明目标,与传统使用旋转毛玻璃产生赝热光的原理相同,硫酸纸的颗粒度改变了激光的空间相干性,使其旋转用来改变光源的时间相干性.目标到毛玻璃的距离u在35—60 cm范围内.相机到散射介质的距离u0在3 cm范围内.小孔直径1 mm,用来控制相机接收的散斑大小和系统成像分辨率.目前手机相机的像素达到千万量级,同时像元尺寸小,此实验只需采集一帧散斑就可成像.因此,在实验中使用手机相机(荣耀9黑白相机,像元尺寸为1µm)拍摄散斑图.
透过毛玻璃对三个不同目标成像,如图3所示.目标“2”的大小为1.2 mm,目标“F”的大小为0.9 mm,目标“E”的大小为1.1 mm.图3(a),(e),(i)所示为相机拍摄到的包含目标信息的原始散斑图像,虽然对不同的目标散斑颗粒度有所不同,但都与原目标形状没有明显的关系.对散斑图做(3)式的自相关运算,近似得到目标的自相关(图3(b),(f),(j)),然后利用窗口函数取散斑自相关的中心部分,采用HIO相位恢复算法[16]重建出目标图像(图3(c),(g),(k)).与原始目标图像(图3(d),(h),(l))对比,目标被有效地重建,验证了该实验方法的正确性,可在此基础上进一步对运动目标进行成像实验.
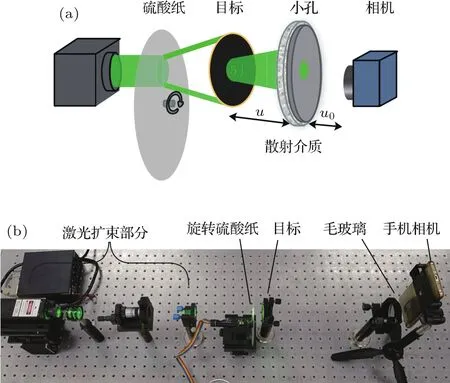
图2 透过散射介质对静止目标成像 (a)实验光路示意图;(b)实验装置实物图Fig.2.Imaging the static object through the scattering medium:(a)Schematic diagram of experimental setup;(b)physical diagram of experimental device.

图3 透过毛玻璃对静止目标成像结果 (a)相机接收的散斑图;(b)散斑图的自相关;(c)重建出的目标图像;(d)原始目标;(e)—(h)和(i)—(l)为对不同目标成像结果,与(a)—(d)一致(比例尺:11个像素)Fig.3.Experimental results of imaging the static object through the ground glass:(a)Raw camera image;(b)the autocorrelation of the raw camera image;(c)reconstructed image;(d)the original object;(e)–(h),(i)–(l)as in(a)–(d)for different objects(scale bars:11 camera pixels).
3.2 运动目标成像
第二组实验是透过散射介质对运动目标成像,我们采用的实验装置(图4(a)和图4(b))与图2中的一致,同样使用旋转硫酸纸改变激光的相干性,转速达到3000 r/min,以减弱背景噪声不一致带来的影响. 选用目标“5”和“2”,目标“5”的大小为1 mm,“2”的大小为1.2 mm.目标在激光束横截面内做水平匀速直线运动,利用软件控制搭载目标的电动平移台在导轨上的运动速度(MC600 motion controller).在目标运动过程中,采集两帧散斑(图4(c)和图4(i)),对散斑做差值运算(图4(d)和图4(j)),然后对散斑差值做(12)式的自相关运算.图4(e)和图4(k)为包含目标运动信息的散斑差值自相关图,图中显示三个目标的相关信息,中间的自相关对应于(12)式的前两项,分布在两边的是目标移动前后的互相关,对应于(12)式的后两项.取图4(e)和图4(k)的中心自相关,如图4(f)和图4(l)所示,利用相位恢复算法,对目标进行重建,如图4(g)和图4(m)所示.与原目标图像对比,有效地重建出了运动目标图像,说明采用散斑差值自相关的方法可以有效减弱运动带来的背景噪声影响,实现对运动目标的清晰成像.
在拍摄目标时,探测器和目标之间发生不同方向或者不同程度的相对运动,得到的图像就会变得模糊,也就是产生了运动模糊.目标的运动造成了散斑颗粒的模糊,在本实验的验证方式中,保持相机不动,曝光时间为1/17 s,系统放大率约为0.0144,目标以一定的速度运动,并允许微小的模糊,理论上,当运动速度约大于2 mm/s时,将产生运动模糊.在实验上,设置不同的运动速度,拍摄运动过程中的两帧散斑图,分别采用散斑差值自相关和散斑相关的方法对运动目标成像.如图5所示,其中,图5(a)—(f)速度为1 mm/s,图5(g)—(l)为2 mm/s,图5(m)—(r)为3 mm/s.采用散斑差值自相关的方法重建目标图像,如图5(d),(j),(p)所示,峰值信噪比分别为15.8478,15.3669,14.7859 dB;采用散斑相关的方法重建的目标图像,如图5(e),(k),(q)所示,峰值信噪比分别为15.9009,15.2670,14.6746 dB.两种方法所得图像质量差别不大,但随着运动速度的增大,采用散斑差值自相关的方法可以较为有效地消除噪声的影响,获得成像质量较高的重建图像.信噪比随着目标运动速度的增大而减小,当目标运动速度为3 mm/s时,散斑差值自相关图中背景噪声随之增大,使得散斑场开始解相关[21],如图5(n)和图5(o)所示,散斑差值自相关图变得模糊,成像效果变差,运动模糊使得成像能力退化.

图4 透过毛玻璃对运动目标成像 (a)实验光路示意图;(b)实验装置实物图;(c)目标运动过程中采集的两帧散斑图;(d)两帧散斑的差值图;(e)散斑差值自相关;(f)取(e)图的中心部分;(g)重建出的运动目标图像;(h)原始目标图像;(i)—(n)与(c)—(h)一致,为对不同目标的成像(比例尺:15个像素)Fig.4.Imaging the moving object through the ground glass:(a)Schematic diagram of experimental setup;(b)physical diagram of experimental device;(c)captured two frame speckle patterns in the process of motion;(d)difference image;(e)autocorrelation of the difference image;(f)the central part of(e);(g)reconstructed moving object;(h)the original object;(i)–(n)as in(c)–(h)for a different object(scale bars:15 camera pixels).
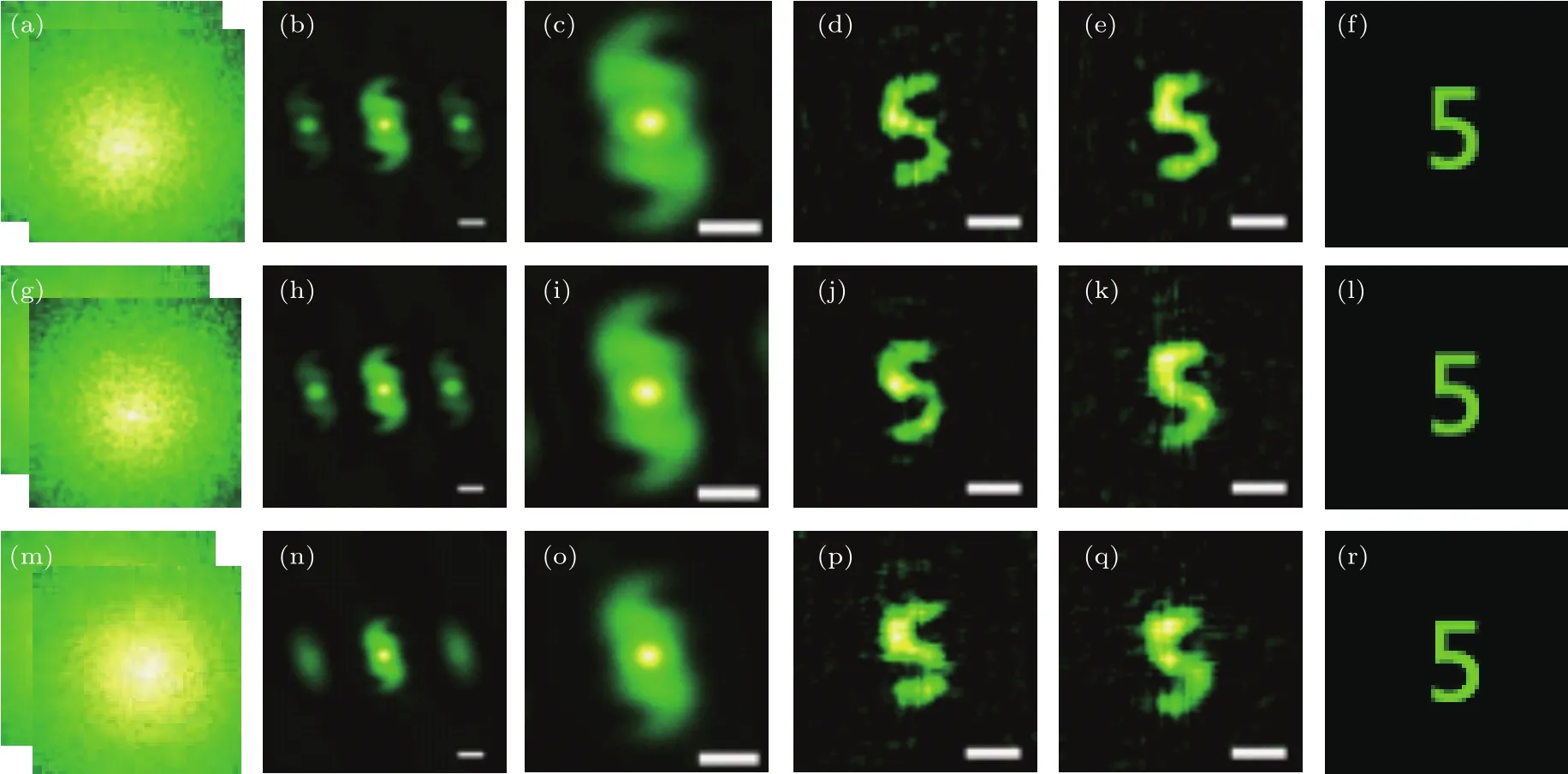
图5 对不同运动速度的目标成像 (a)目标运动速度1 mm/s,运动过程中采集的两帧散斑图;(b)散斑差值自相关;(c)取(b)图的中心部分;(d)重建出的运动目标图像;(e)采用散斑相关的方法重建出的运动目标图像;(f)原始目标图像;(g)—(l)与(a)—(f)一致,速度为2 mm/s;(m)—(r)与(a)—(f)一致,速度为3 mm/s(比例尺:15个像素)Fig.5.Imaging the moving object with different speeds:(a)Captured two frame speckle patterns with the speed of 1 mm/s in the process of motion;(b)autocorrelation of the difference image;(c)the central part of(c);(d)reconstructed moving object;(e)reconstructed moving object with the method of speckle correlation;(f)the original object;(g)–(l)as in(a)–(f)with the speed of 2 mm/s;(m)–(r)as in(a)–(f)with the speed of 3 mm/s(scale bars:15 camera pixels).
3.3 目标运动距离计算及跟踪
第三组实验为透过散射介质对目标运动距离进行测量,实验装置如图4(b)所示,选用目标“5”作为测量对象,u=520 mm,u0=7.6 mm,N0=15,A=1µm,代入(13)式计算得到目标大小y=1.026 mm,目标实际大小为1 mm.实验中,采用MC600运动控制器,设置目标运动速度1 mm/s.每移动1 mm,拍摄一帧散斑图,如表1所列,目标实际总移动3 mm,通过(14)式计算得到目标移动距离∆x′=3.010 mm.误差的存在是由于距离测量和像素数所引起的.

表1 目标“5”的实际运动距离和实验测量结果Table 1.Actual moving distance and experimental results with object “5”.
随着目标的运动,每隔1 mm采集的散斑,分别与第一帧散斑做差值,然后做自相关,在散斑差值自相关图中,目标互相关出现在不同位置,位于图中的两侧,如图6(a)—(c)所示,第一行为散斑差值自相关图,第二行分别对应散斑差值自相关图中心虚线处的强度分布.根据(14)式计算移动后的目标到初始位置的距离,可以对目标进行实时追踪,追踪精度满足A/β,此实验中追踪精度可达到68.42µm,通过增大放大率的方法可以提高追踪精度,但增大放大率将会增大散斑颗粒的模糊程度而使成像效果变差.自相关和互相关中心处光斑能量最高,可根据中心亮斑的强度定位目标位置,互相关的峰值强度比自相关低,这是因为自相关信息是两部分的叠加,如(12)式所表示.另外,由于散斑采集间隔的影响,导致系统PSF的相关性降低及拍摄的散斑图强度存在差别,用(12)式对散斑做差值自相关,理论与实际存在差别,如图6第二行所示,随着目标运动距离的增加,两帧散斑图能量差别较大,背景噪声随之增大.当采集的两帧散斑在一个记忆效应角范围外时,将导致互相关能量较低、背景噪声太大而检测不到强度对比信息,因此,应保证采集的相邻散斑在一个记忆效应角度范围内.
4 讨 论
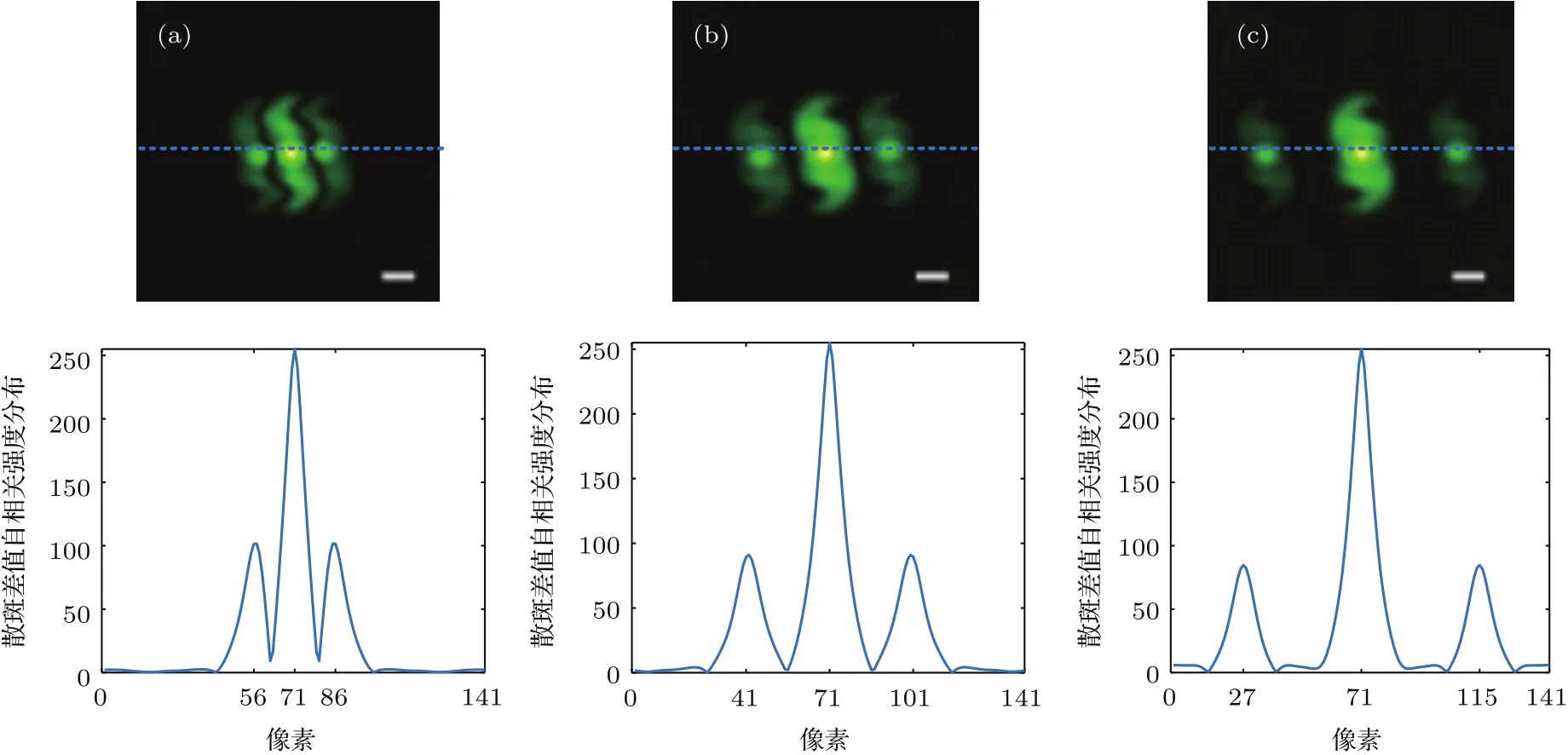
图6 对目标实时追踪 (a)—(c)上图为目标运动过程中自相关和互相关的位置关系图;下图分别对应上图中心处的强度分布(比例尺:15个像素)Fig.6.Tracking the moving target in real-time:(a)–(c)First row:position relationship of the autocorrelation and cross-correlation;second row:intensity value of horizontal direction across the central point of the first row(scale bars:15 camera pixels).
根据(1)式的散斑相关度公式,基于光学记忆效应的散斑相关成像方法的光学记忆效应角满足δθ<λ/(πL),角度范围与散射介质的有效厚度成反比,该方法适用于薄散射介质,通常有效厚度远小于1 mm.目标大小需要在记忆效应角度范围内,δl≪uλ/(πL),当目标运动范围超过一个记忆效应角度,拍摄的两帧散斑相关度降低,导致散斑差值自相关图中背景项增大.因此,在实验中,采用散斑差值自相关对运动目标成像及追踪,采集的相邻两帧散斑需保证在一个记忆效应角范围内,以便获得高相关度的散斑,保证计算出的运动距离更精确.其中,目标运动范围受限于激光束的的扩束直径及能量分布;另外,相机的视场角及相机前的小孔同样限制了目标运动范围.
对于目标运动速度,当相机像元尺寸(A)一定,目标运动速度(v)和曝光时间(∆t)满足v×∆t×β 6 A时,没有运动模糊产生,可清晰成像.在实验上,可允许一定的运动模糊,采用手机相机拍摄散斑图,系统自动匹配曝光时间(1/17 s),最大可对速度为7 mm/s的目标成像及追踪.若要对更高速度的运动目标成像及追踪,需采用高帧频的相机拍摄散斑图来减小曝光时间,以便应对速度在cm/s量级的运动目标;另外,若对散斑图做去模糊处理,甚至可对m/s量级的运动目标成像及追踪.
5 结 论
基于散斑差值自相关方法,本文提出了一种透过散射介质对运动目标的全光成像及实时追踪技术,用实验验证了其可行性,并给出了目标运动距离的计算公式.实现中,可用低价匀光片代替昂贵的空间光调制器产生赝热光,根据应用需求对透射和反射式目标进行成像及追踪,目标大小应满足条件对于不同尺寸的目标,需调整散射介质到目标的距离u以获得清晰的像.若距离太近,系统放大率增大,会造成散斑颗粒的模糊,导致信噪比降低,成像质量变差.为避免图像产生运动模糊,目标运动速度应满足v×∆t×β 6 A条件.采取高帧频的相机拍摄散斑图并对散斑图进行去模糊处理,可实现对m/s量级的运动目标的成像及追踪,目标追踪精度满足A/β.此外,激光束扩束直径及能量分布、相机的视场角等因素会限制目标运动范围,设计成像系统时应加以考虑.影响成像质量的因素有相机分辨率、系统放大率、散射介质的有效厚度和图像重构算法等.相机处的每个散斑颗粒都应满足奈奎斯特抽样定理,同时还应采用高分辨相机,使在每个图像中俘获的散斑颗粒的数量最大化以便减小背景噪声;为获得高保真度的目标图像,除了文中提及的Fienup基本相位恢复算法外,还可采用基于双谱计算的散斑重建[5]等方法,来提高算法的鲁棒性,得到更稳定的图像.如何对任意轨迹目标成像并提高成像质量,将成为下一步的研究重点.
本文探讨的透过散射介质对直线运动目标全光成像及追踪技术,在视网膜白内障诊断、在稀疏变薄的颅骨下可视化脑组织等生物医学诊疗等领域具有广阔应用前景.
