致密气藏压裂水平井产能分析及压裂优化设计

2018-12-18孙元伟程远方时凤霞王艳丽印树明

新疆石油地质 2018年6期

孙元伟，程远方，时凤霞，王艳丽，印树明

（1.中国石油大学胜利学院油气工程学院，山东东营 257061；2.中国石油大学石油工程学院，山东青岛 266580）

近年来，随着水平井压裂技术的不断发展，致密气藏的开采在全世界范围内取得了巨大突破，成为油气增产的主阵地[1-2]。致密储集层具有渗透率低、应力敏感性较大等特点，开发过程中渗透率等物性参数随着应力场而改变，这些变化又反作用于储集层流体的流动[3-5]。由于致密储集层初始渗透率相对较小，应力对渗透率造成的微小变化会对产能产生较大的影响，因而对致密储集层进行应力敏感性研究具有重要意义。

许多学者对应力敏感储集层流体渗流进行了研究：文献［6］和文献［7］描述了压敏介质非线性不定常渗流数学模型，给出了稳态渗流解析解及非稳态渗流数值解；文献［8］采用小扰动等方法求解压敏介质非线性渗流数学模型。以上研究结果对应力敏感储集层渗流机理进行了分析，但是对于开发效果研究较少。文献［9］首次采用三线性流模型描述致密气藏水力裂缝渗流机理以及产能变化规律；文献［10］将三线性流模型与文献［11］的三维数值模拟模型进行了对比，并优化了裂缝参数；文献［12］和文献［13］对三线性流模型进行了发展完善，但是均没有考虑应力敏感性对致密气藏开发效果的影响。

针对以上研究的不足，基于应力敏感性对致密储集层渗透率的影响，建立了致密气藏压裂水平井三线性流耦合模型。在验证模型正确性的基础上，绘制了水平井分段压裂产能变化曲线，分析了产能的影响因素，并设计正交试验确定产能影响主控因素。

1 考虑应力敏感性的致密气藏渗流模型

基于分段压裂水平井三线性流模型（图1），考虑致密气藏应力敏感性对流体渗流的影响，建立致密气藏渗流模型。假设流体在气藏中的渗流过程分为3个阶段，裂缝间改造区域为影响产能主要区域，采用缝网双重介质模型描述其渗流规律，并且假设缝网双重介质中基质与裂缝之间为拟稳态流动。

图1 分段压裂水平井三线性流模型

对致密气藏进行渗流分析时，为了精确表征其渗流规律，引入拟压力的概念[14]：

文献［15］和文献［16］通过实验拟合储集层应力与渗透率的关系，得到考虑应力敏感性时储集层渗透率变化方程：

为方便计算，定义无因次参数如下。

无因次拟压力：

无因次时间：

对图1中人工裂缝区域渗流规律进行分析变换，可以得到其流体无因次拉普拉斯空间渗流方程：

图1中裂缝间改造区域采用缝网双重介质模型描述其渗流规律，该区域流体无因次拉普拉斯空间渗流方程为

图1中储集层未改造区域流体的无因次拉普拉斯空间渗流方程为

（5）式—（7）式为非线性方程，无法对其进行直接求解，采用摄动技术对其进行简化求解，定义：

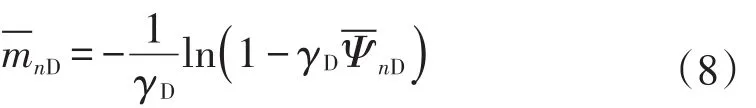
将（5）式—（8）式联立，假设水平井定产量生产，外边界封闭，则可以得到在拉普拉斯空间内的无因次井底压力表达式

在拉普拉斯空间求得压力解，利用Stehfest数值反演方法[17]，便可得到真实空间解。定井底流压生产则压裂水平井产量为

2 模型验证

通过压力恢复、资料解释等手段，获得了胜利油田某致密气藏储集层相关参数（表1）。利用储集层数据计算井底压力，并与实测压力进行拟合（图2）。从图2中无因次压力及其导数曲线可以看出，气体在渗流过程中经历了井筒存储、线性流、拟径向流等阶段，计算结果与实际测量结果拟合较好。但实际试井曲线在生产后期有一定的波动，这是由于生产受到一定干扰引起的。

3 致密气藏压裂水平井产能分析

将该模型应用到胜利油田某致密气藏，研究裂缝长度、裂缝间改造区域渗透率、裂缝间距等压裂参数对水平井产能的影响。

表1 胜利油田某致密气藏储集层参数

图2 胜利油田某致密气藏压裂水平井模型验证

3.1 裂缝半长对产能的影响

分别考虑裂缝半长为20 m，30 m，40 m，60 m，80 m和100 m时，计算不同时刻的累计产气量（图3）。从图3可以看出，随着裂缝半长的增加，累计产气量增加，但增幅越来越小。主要原因是裂缝越长，储集层泄气面积越大，气井产量增加；当裂缝长度增加到一定程度之后，受储集层边界等因素的影响，储集层泄气面积增加幅度将会减小，产能增幅下降。

图3 胜利油田某致密气藏裂缝长度对产能的影响

3.2 裂缝间改造区域渗透率对产能的影响

分别考虑裂缝间改造区域渗透率为1 mD，5 mD，10 mD，15 mD和20 mD时，裂缝间改造区域渗透率对致密气藏单井产能影响（图4）。从图4可以看出，裂缝间改造区域渗透率越大，储集层累计产气量越大，但增幅变化规律不一致：当改造区域渗透率小于10 mD或者大于15 mD时，累计产气量增幅影响较小；当改造区域渗透率为10～15 mD时，累计产气量增幅较大。产量增幅影响较小的主要原因在于人工裂缝并非无限导流，当储集层改造区域渗透率增加到一定程度后，受人工裂缝导流能力的限制，继续增加改造区域渗透率对产能影响较小。

图4 胜利油田某致密气藏裂缝间改造区域渗透率对产能的影响

3.3 裂缝条数对产能的影响

假设水平井筒长度为1 000 m，裂缝均匀分布，分别为3条、4条、5条、6条和7条，可以得到裂缝条数对致密气藏单井产能影响（图5）。从图5可以看出，裂缝条数越多，单井累计产量越大，随着裂缝条数的增加，产能增幅越来越小，当裂缝条数大于6条之后，继续增加裂缝条数对产量增幅影响极小。其主要原因在于当裂缝条数较多时，裂缝间距小于一定程度后，裂缝间的干扰加剧，继续减少裂缝间距对产量增幅影响越来越小。

图5 胜利油田某致密气藏裂缝条数对产能的影响

4 致密气藏压裂参数敏感性分析

裂缝长度、裂缝间距、裂缝间改造区域渗透率等因素对致密气藏水平井产能产生较大影响，可通过正交试验，确定各因素对产能影响的主次关系。分别设计裂缝间改造区域渗透率为5 mD，10 mD，15 mD和20 mD，裂缝半长为40 m，60 m，80 m和100 m，裂缝间距为100 m，200 m，300 m和400 m的情况下，通过正交设计得到16种方案（表2）。通过对各方案水平井产能计算结果进行极差分析可以看出，对致密气藏水平井产能影响排序为：裂缝间改造区域渗透率最大，裂缝长度次之，裂缝条数最小。

表2 胜利油田某致密气藏正交试验方案设计及水平井产能计算结果

5 致密气藏压裂水平井参数优化

图6 胜利油田某致密气藏单井累计产气量与裂缝条数关系

通过对致密气藏压裂水平井产能影响因素正交试验结果表明，裂缝间改造区域渗透率对单井产能影响最大，而图6和图7分别对该气藏裂缝条数及裂缝半长进行优化设计。从图6可以看出，单井产量随着裂缝条数的增加而增加，当裂缝条数增加到6条之后，单井产量增加速度变小，因此最优裂缝条数为6条。从图7可以看出，裂缝半长为140 m之后，继续增加裂缝长度，单井产量增加速度变小，综合考虑压裂成本等因素，最优裂缝半长为140 m.综上所述，在对该区块进行压裂设计时，在裂缝半长为140 m，裂缝密度为6条/km时，尽量增大改造区域渗透率，可以获得最佳产量。