加筋肋薄壁机匣振动及强度综合优化设计
2018-12-18艾延廷赵金明
艾延廷 ,王 亮,田 晶,赵金明
(1.沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室,辽宁 沈阳 110136;2.中国南方航空股份有限公司沈阳维修基地,辽宁 沈阳 110169)
1 引言
航空发动机机匣为典型的薄壁结构,是发动机的主要承力件,也是形成发动机气流通道的主要构件。在工作过程中,薄壁机匣由于受到多种复杂载荷的作用会产生一系列振动和疲劳破坏问题。因此,在发动机设计阶段,机匣的振动和疲劳破坏问题倍受关注。设计者往往要综合考虑发动机机匣减振、提高强度以及减轻质量等重要设计目标。如何迅速、准确地分析和预测发动机机匣结构的动力学特性,并针对设计要求对其进行综合优化设计,使发动机机匣各项性能综合达到一个较高水平显得十分重要。
近年来,国内外学者针对航空发动机机匣振动和强度分析、模态试验及优化设计等问题进行了研究[1-4]。文献[5-6]首先推导出了满足固有频率约束的动力优化设计准则,并利用准则方法对具有频率约束的框架结构进行了优化。文献[7]分析某涡扇发动机风扇机匣的振动过大现象,研究减振措施,在此基础上提出了风扇机匣结构的自主优化设计方法,以减小风扇机匣的振动问题,优化结果显著。文献[8]基于遗传算法,以结构应力为目标函数,以固有频率为约束条件,对加筋圆柱壳进行了动力优化。文献[9-10]分别基于结构面板声功率贡献量的分析方法和Hamilton原理对直升机机匣及桨叶进行了减振优化设计。上述文献只是基于单目标进行了优化,虽然优化效果显著但没有考虑到优化结果可能对其他因素造成的影响。文献[11]通过有限元对多种加肋机匣的振动特性进行了分析,并通过实验验证了结果的正确性。以减振和提高疲劳强度为目标,对薄壁机匣加筋肋进行的综合优化设计。首先,采用有限元软件建立模型,对薄壁机匣结构进行振动分析,并通过模态试验与计算结果相对比验证了计算模型的准确性。其次,对加筋肋位置、几何尺寸进行优化设计,采取正交试验设计方案对设计变量进行优化,并对优化结果的准确性进行试验和有限元计算验证。最后,对加筋肋薄壁机匣的振动和强度进行综合优化设计。将响应面法与正交试验设计相结合,通过模态试验验证优化方法,为发动机薄壁机匣结构减振及提高强度等综合设计提供了参考。
2 有限元模态分析与试验验证
2.1 有限元模态分析
建立机匣有限元模型,如图1所示。薄壁机匣由机匣外环、内环及4根支板组成。外环端面内壁直径494mm;机匣壁厚3mm;机匣总长200mm;法兰厚度4mm;支板厚度3mm。利用WORKBENCH软件建立薄壁机匣模型,根据环向加肋机匣模型特点,采用Edge Sizing和Hex Dominant Method方法进行网格划分。将支板与螺栓孔切割出来进行网格的单独化分,最小网格边界长度为(1.3057×10-10)mm。薄壁机匣结构有限元模型材料采用45#钢,其弹性模量为2.0E5MPa,密度为7850kg/m3,泊松比为0.3。

图1 薄壁机匣有限元模型Fig.1 Thin-Wall Casing Model
2.2 模态试验
薄壁机匣远离支板一端固定,另一端自由,分别在内环、支板以及外壁上优化选取三个测点安装三个加速度传感器。采用锤击法进行模态试验,同时进行加速度和力信号的采集,通过LMS进行数据处理和分析。试验仪器包括LMS振动测量和分析系统及其配套的Test Lab软件、力锤、加速度传感器等,如图2所示。

图2 试验系统Fig.2 Testing System
试验时激振点的选取应能激起结构的各阶模态,避免选在结构节点处。由于试验件整体尺寸较大,为避免实验过程中模态被遗漏,在实验件不同位置粘贴了3个传感器。试验件被划分为480个测点,在每根支板上取15个点,共60个点,内环划分为60个点;外壁划分为360个点,如图3所示。

图3 试验简化模型Fig.3 Simplified Test Model
2.3 计算与试验结果对比分析
通过试验测得结构的前15阶振动模态,经过分析处理后提取薄壁机匣四阶典型振型,如图4所示。图中左侧线形图为试验测得振型,右侧云图为有限元计算振型图。由图4可以看出,机匣振动方式主要以外壁的弯曲振动和支板的扭振为主,试验与有限元计算结果,如表1所示。
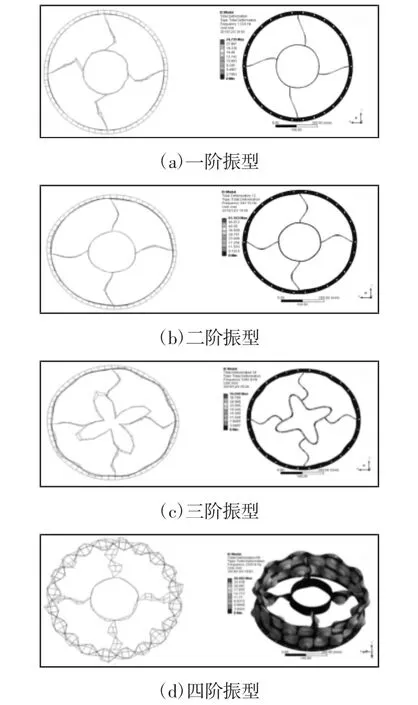
图4 试验与有限元振型对比图Fig.4 The Test and Finite Element Modal Shape
由图4和表1可以看出,选取的薄壁机匣4阶典型振型的有限元计算结果与试验结果基本一致,各阶误差全部在4%以内。

表1 试验与有限元计算值Tab.1 Vibration Value of the Casing
3 响应面法及综合优化流程
3.1 响应面法介绍
响应面法是由英国统计学家G.Box和Wilson于1951年提出的。响应面法是指研究变量与性能指标之间存在非线性关系时,利用试验设计的方法得到响应的数据,采用多元二次回归方程拟合响应值和因素之间函数关系的一种优化统计方法。响应面法具体步骤包括确立目标函数、建立数学模型、数据结果分析和优化。其优化流程,如图5所示。

图5 优化设计步骤Fig.5 Optimization Design Steps
试验过程中由于受到诸多因素的影响,不同因素的重要性在初始研究过程中难以辨别,进行筛选,去除不重要因素。可以通过正交组合设计来实现。一旦判别其重要因素只有少数几个时,可将试验分为两个阶段。首先,判断已知的试验条件和输入变量的水平能否趋近于响应面的最优位置。如果远离其最优位置时,一般选取一阶模型去逼近:

式中:βi—编码变量xi的线性效应。
能使公式系数可估的设计称为一阶设计。
假如试验部分接近或处于响应面的最优区域时,则进行第二阶段设计,即采用二阶模型来逼近,

式中:βi—xi的线性效应;βij—xi与 xj之间的交互作用效应;βii—xi的二次效应。
3.2 基于响应面法的综合优化设计
综合优化设计即多目标优化,是对目标函数进行统一处理从而进行优化。多目标优化问题得到的可能只是较优解,而较优解往往会存在很多个,需要在多个解中找出一个最优解。多目标优化问题的解法主要包括直接法和间接法。
直接法是直接求出较优解,然后再比较选择出最好的解。间接法是将多目标优化问题转化为单目标优化问题,包括线性加权和法、统一目标函数法和理想点法等。
统一目标函数法就是设法将各单目标函数整合构成一个新的目标函数f(X),这样就把原来的多目标问题转化为一个具有统—目标函数的单目标问题来求解,即:
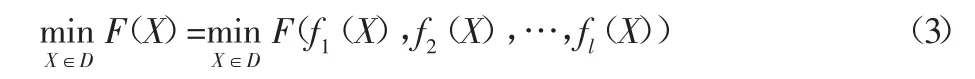
式中:D—可行域;f1(X),f2(X),…,fL(X)—各个子目标函数。
然后根据各子目标对优化结果影响的重要程度设定相应的权数,然后用各子目标分别乘以各自的权数,再求和即构成新的统一目标函数,即总体目标函数:

式中:f1(X),f2(X),…,fL(X)—各子目标函数;ω1,ω2,…,ωL—权数,ωi应满足归一性和非负性条件。

建立该目标函数时,需进行各子目标函数权数的确定和无量钢化处理,权数的确定根据相应目标函数在优化模型中的重要程度决定。无量钢化处理如下式:

4 基于振动特性的优化设计
4.1 优化目标与优化设计变量的选取
通过有限元分析计算,发现第四阶振型在肋面出现了明显的共振,在实际发动机工作状态下气流激振可以很容易激起该阶振型,进而造成机匣的振动破坏。为避免机匣破坏,可以通过优化计算使得该阶振动频率避开某个频率带。以优化该阶频率高于某个值为例进行研究。选择优化目标为:使该阶频率大于无肋时该阶振型的频率,即在保证加筋肋截面尺寸不变的情况下,使该阶频率y1i>2393.6Hz。优化目标的振型,如图6所示。

图6 作为优化目标所选取的某阶振型Fig.6 OptimizationFinite Element Modal Shape
本部分主要研究以环向肋的位置和截面积尺寸为参数优化薄壁机匣的振动特性。选取设计变量环向加筋肋的高度为b、宽度为c和环向肋距右端距离为a。
根据实验件的结构及几何尺寸,选取设计变量的变化范围,如表2所示。

表2 设计变量取值范围Tab.2 Design Variables
4.2 振动特性优化试验设计
采用正交试验设计方法,对设计变量进行正交组合试验设计,采用Ansys Workbench有限元软件进行参数化建模和数值计算,求得目标函数值与设计变量之间的对应关系。按照Box-Behnken Design理论,根据正交试验设计表的数据特点,选择合适的数据拟合模型进行数据拟合及回归分析,得到用设计变量表示目标函数的响应面模型,式(8)为环向肋几何结构参数与第四阶频率的函数关系式。
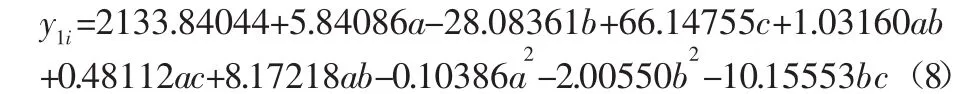
4.3 优化结果
采用基于BBD设计的响应面优化方法对薄壁机匣环向加肋的振动特性进行优化设计,在保证加筋肋截面积为24mm2不变的情况下,经过圆整处理,得到结构各项最优几何参数,如表3所示。

表3 振动优化结果Tab.3 Optimization Result of Vibration
4.4 优化结果试验验证
根据优化结果设计加工了环向加肋薄壁机匣试验件。具体试验方法及过程设置与无肋薄壁机匣模态试验相同,试验结果与有限元对比,如图7所示。
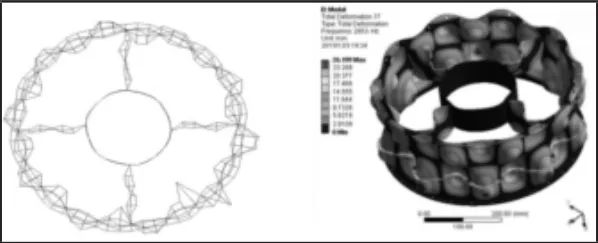
图7 优化结果试验与计算振型对比Fig.7 Optimization Result of the Test and Finite Element Modal Shape
将优化结果带入有限元计算,得出第四阶频率为2853.0Hz,模态试验得出该阶频率为2891.4Hz,优化后第四阶固有频率得到了显著的提升。试验数据与有限元计算结果对比证明了基于响应面法优化的准确性及优化效果的显著性。保证加筋肋截面形式为(8×3)mm计算不同位置下该阶固有频率,如表4所示,保证加筋肋位置75mm计算不同截面形式下该阶固有频率,如表5所示。

表4 不同肋位置频率值Tab.4 Frequency Values at Different Positions of Rib

表5 不同肋截面尺寸频率值Tab.5 Frequency Values of Different Rib Size
从表4和表5中得出在保证加筋肋截面面积不变的情况下,在该优化结果下加筋肋薄壁机匣四阶频率为最大值,说明优化结果准确可靠。
5 基于强度特性的优化设计
5.1 优化目标与优化设计变量的选取
对进气道机匣的受力情况分析表明,薄壁机匣外壁面容易受到破坏,因此选择薄壁机匣外壁面的最大等效应力作为优化目标。模拟实际进气道机匣在内环轴承安装座处受力情况,对计算模型轴承内环上半面施加幅值为10000N呈半正弦曲线分布的径向力,如图8所示。
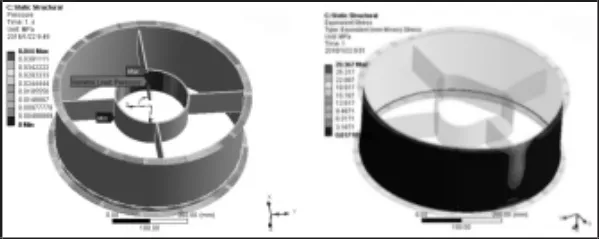
图8 载荷施加图Fig.8 Boundary Condition
根据实验件的结构及几何尺寸,选取设计变量的变化范围,如表2所示。
5.2 强度特性优化实验设计
本部分所采用的实验设计方法与振动特性优化设计相同,即采用正交试验设计方法,式(9)为环向肋几何结构参数与外壁最大等效应力的函数关系式。

5.3 优化结果
同样是保证加筋肋截面积为24mm2不变,经圆整,得到结构最优几何参数,如表6所示。

表6 优化结果Tab.6 Optimization Results of Strength
5.4 优化结果有限元验证
将优化结果带入有限元进行计算,得出薄壁机匣外壁面最大等效应力为25.8MPa,优化后薄壁机匣外壁面强度显著提高。保证加筋肋截面形式为(8×3)mm计算不同位置下外壁强度,如表7所示。保证加筋肋位置90mm计算不同截面形式下外壁强度,如表8所示。

表7 不同肋位置强度值Tab.7 Intensity Values at Different Positions of Rib

表8 不同肋截面尺寸强度值Tab.8 Intensity Values ofDifferent Rib Size
通过表7和表8可以得出在保证加筋肋截面面积不变的情况下,在该优化结果下外壁强度为最大值,说明优化结果准确可靠。
6 加筋肋薄壁机匣综合优化设计
6.1 加筋肋综合优化目标与设计变量选择
选择影响较为显著的振动特性和外壁强度特性作为优化目标,采取统一目标函数法进行多目标优化,优化设计变量选取的范围与振动特性优化相同,如表2所示。
6.2 统一优化目标函数
对振动特性目标函数与强度特性目标函数进行处理,设优化所选的目标函数为Y。

先进行无量纲处理,然后根据两个目标的重要程度给予相应的权数,由于振动特性对薄壁机匣影响较大,可设振动特性及强度特性的权重数分别为ω1=0.8、ω2=0.2。
在强度计算时所选取的是外壁的最大等效应力,等效应力越大表示外壁强度越小,而固有频率优化目标为大于该阶固有频率,优化时设定选取最大值优化。因此,将强度特性目标函数取倒数带入综合优化函数中,形成统一优化目标函数。
6.3 综合优化试验设计
综合优化采用的实验设计方法与振动特性优化相同,即正交试验设计方法,式(11)为环向肋几何结构参数与优化目标Y的函数关系式。

6.4 综合优化结果
同样保持加筋肋截面积不变,进行综合优化,优化结果,如表9所示。

表9 综合优化结果Tab.9 Comprehensive Optimization Results
6.5 综合优化结果对比分析
将单目标优化和综合优化结果带入有限元中计算得出薄壁机匣的各项数据,如表10所示。

表10 优化结果对比Tab.10 The Contrast of Optimization Results
从表10中可以看出,综合优化在振动及强度单方面虽然无法达到单目标优化的结果,但固有频率和外壁强度综合达到一个比较好的结果。能够根据设计的要求来平衡两种性能。
7 结论
(1)通过有限元软件建模与计算,得到环向加肋薄壁机匣振动特性和结构强度,通过与模态试验结果对比,计算误差小于4%,证明有限元方法计算的准确性。(2)将响应面法与正交试验设计相结合,通过模态试验验证优化方法及结果,为发动机薄壁机匣优化方法设计提供了参考。(3)对加筋肋的位置和截面尺寸进行单目标优化时,优化结果显示在等质量的情况下单目标优化可以使振动特性或者强度特性分别达到最优值,可以根据实际情况的不同要求选择加筋肋的位置及形式。(4)采用线性加权平均法对环向加肋薄壁机匣的振动特性及外壁强度进行综合分析,并对加肋的位置及截面尺寸进行优化综合设计,优化结果显示在等质量的情况下,综合优化可以根据振动及强度的要求对加筋肋的位置及形式进行优化,使薄壁机匣的减振及强度同时达到设计要求,为环向加肋薄壁机匣的综合设计提供指导。
