考虑轮胎侧偏刚度的后驱汽车转向中心研究

2018-12-18廖林清陈荣中

机械设计与制造 2018年12期

王伟，廖林清，张君，陈荣中

（1.重庆理工大学机械工程学院，重庆 400054；2.重庆理工大学汽车零部件制造及检测技术教育部重点实验室，重庆 400054；3.南方天合底盘系统有限公司，重庆 402760）

1 引言

理想阿克曼转向原理是将轮胎视为刚体，忽略侧偏力的影响，从最理想状态分析汽车纯滚动转向的条件，确定汽车的转向中心。但实际中轮胎不是刚体，故汽车转向行驶中受侧向力的作用必定会产生侧偏角。目前，国内学者研究聚焦于轮胎的侧偏特性[1-3]，而对于转向特性的侧偏影响研究多集中在基于多体动力学软件进行的仿真与优化[4-5]；国外学者则对多轴汽车转向阿克曼转向原理进行了修正[6-8]，而对于考虑轮胎侧偏刚度下汽车低速转向行驶时的转向理想条件基础理论并没有涉及。对汽车低速转向行驶时的转向理想条件以及已知任意前瞬心点时后驱汽车转向中心进行了研究。

2 阿克曼转向原理的修正

2.1 阿克曼转向原理

为了避免汽车转向时路面产生附加阻力和轮胎磨损过快，要求转向系统能保证汽车转向时所有车轮均作纯滚动运动，车轮转向角满足阿克曼转向原理，即在汽车前轮定位角都为零、车轮为刚性的前提下，所有车轮在整个转向过程中围绕同一瞬时中心转动[9]，此瞬时中心即为汽车转向中心，其转向角需满足式（1）。

式中：α、β—汽车转向时的外轮和内轮转角；l、b—汽车轴距和主销间距。

2.2 阿克曼转向原理的修正

理想阿克曼转向原理在考虑轮胎侧偏刚度后会出现偏离，以后驱汽车为例，据文献[10-12]建立汽车转向力学模型，对理想阿克曼转向原理进行修正。后驱汽车侧偏示意图，如图1所示。考虑轮胎侧偏刚度后，汽车的前轮瞬心点将从A偏离到B。此时汽车转向并不满足理想阿克曼转向关系，为使转向汽车车轮作纯滚动运动，须预先给前轮一个预偏角来抵消其侧偏角，使前轮瞬心点刚好落在后轮轴线上。

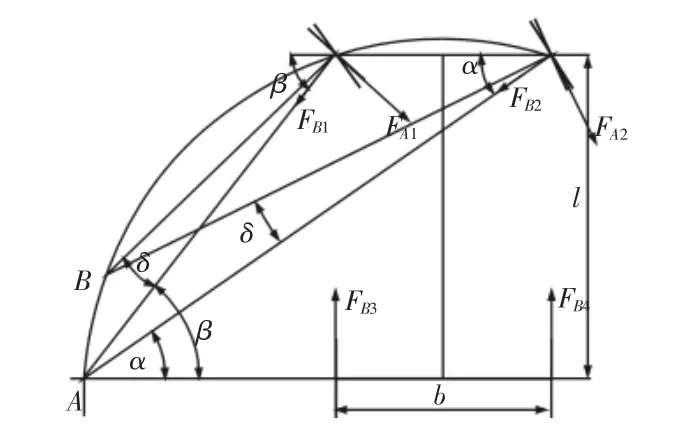
图1 后驱汽车侧偏示意图Fig.1 The Side-Slip Drawing of Rear Drive Vehicle

由分析可得此时的转向角关系应满足：

式（2）即为修正后的阿克曼转向原理，式中：δ—前轮预偏角；因前驱汽车前轮瞬心点侧偏后落在汽车后轴线下方，前轮预偏角的方向与后驱汽车刚好相反，故前轮预偏角δ前的符号可正可负，我们定义前驱汽车预偏角δ前的符号为正，后驱汽车预偏角δ前的符号为负。

3 后驱汽车转向理想线的定义及求解

3.1 汽车转向理想线的定义

汽车转向行驶时前轮发生了侧偏，而后轮没有侧偏，此时不是所有车轮都作纯滚动运动。为使汽车转向时为所有车轮均作纯滚动运动，需使汽车前轮侧偏后前轮瞬心点刚好落在后轮轴线上。因此预先给前轮一个预偏角使侧偏后前轮瞬心点刚好落在后轮轴线上。不同的两前轮转角对应着不同的预偏角即对应着不同的前轮瞬心点，将这样一系列给定预偏角后所对应的前轮瞬心点的连线称为汽车转向理想线。

3.2 后驱汽车转向理想线的求解

建立后驱汽车力学模型，如图2所示。其中图示参数，如表1所示。可得：

式中：F—滚动阻力，F=FA1＝FA2。

图2 后驱汽车力学模型Fig.2 The Driving Force Model of Rear Drive Vehicle

表1 后驱汽车受力模型参数Tab.1 The Stressed Parameters of Rear Drive Vehicle

由汽车转向受力平衡方程解出的汽车驱动力、轴向力的大小只与汽车两前转向轮转角的大小相关，与汽车的坐标系无关。因此为求得汽车前瞬心线，将横坐标定义在汽车的后轴线上，向右为正；纵坐标与汽车左右对称线重合，向上为正。将汽车侧偏后的前瞬心线作汽车后轴线的对称线。可以得到前瞬心对称后的坐标为：

带入某车型参数有：

后驱汽车预偏后的前轮瞬心线偏离中可以看出，无论是大转角还是小转角，前轮瞬心线与后轮轴线的偏离比较小，趋于0，如图3所示。

图3 预偏后后驱汽车的前瞬心线偏离Fig.3 The Deflection of the Rear Drive Vehicle’s Front Instantaneous Center Line After Given the Bias Angle

实线表示后驱汽车预偏角与预偏后的侧偏角的关系，虚线为与水平轴成45°的直线，由图可看出后驱汽车的预偏角和预偏后的侧偏角成线性关系，且与虚线相重合，由此说明后驱汽车给定预偏角后发生的侧偏角和给定的预偏角相等，如图4所示。综合图3和图4，以及汽车转向理想线的定义可知，此种方法求出的后驱汽车转向理想线是可行的。

图4 后驱汽车预偏角与预偏后新的侧偏角的关系Fig.4 The Relationship of the Rear Drive Vehicle’s Bias Angle and New Sideslip Angle After Given the Bias Angle

4 给定前点时后驱汽车转向中心算例

4.1 后驱等效三轮模型的建立与分析

由前面转向理想线分析可知，汽车若按照理想阿克曼转向，前轮必定存在侧偏。而目前现有的转向机构只有一个点满足转向理想线条件，而其它点对应转向中心在哪里我们并不知道。后驱汽车行驶中前轮的轴向力（侧向力）、后轮的驱动力与轴向力都是可以改变的，而切向力（滚动阻力）是不能改变，因此可建立一个新的汽车力平衡关系，使汽车前轮速度瞬心点和后轮速度瞬心点交于一点，此点即为汽车转向中心点。

汽车低速转向行驶时，忽略离心力，将汽车两后轮等效为过汽车左右对称线的一个轮胎，以后驱汽车左转向为例，如图5所示（点划线）等效三轮转向中心力学模型，其中y轴为汽车左右对称线并规定向上为正方向，x轴在汽车后轴线上，规定向右为正方向，图中的参数，如表2所示。

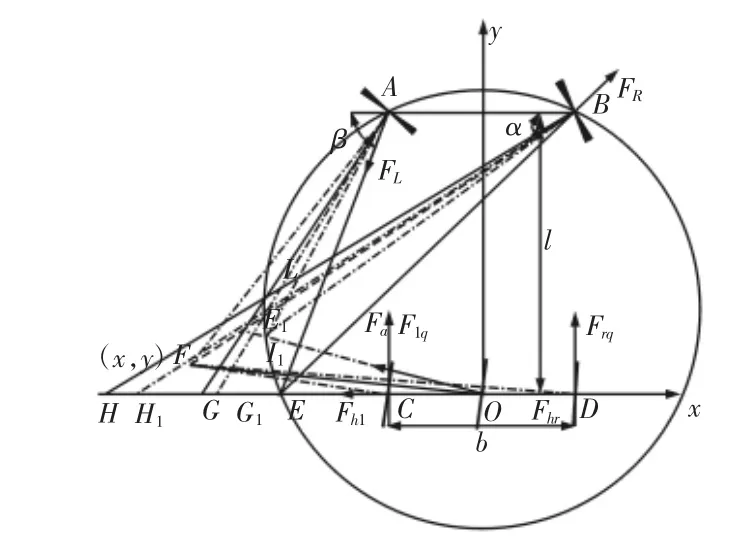
图5 后驱汽车等效三轮模型及四轮模型Fig.5 The Equivalent Three Wheel Model and Four Wheel Model of the Rear Drive Vehicle

假设两前轮侧偏后的侧偏线交于E1点，延长两前轮中心点A、B与E1点的连线交后轮轴线分别于H1、G1两点。由力平衡关系可得，汽车所受力必定汇交于一点。由于两前轮轴向力方向已知，因此等效三轮模型中后轮所受力必定相交于前轮瞬心点。又由侧偏力和侧偏角的关系，前轮瞬心点会变到F点，那么后轮瞬心点必定也只能相交于F点，因此汽车的转向中心即整车瞬心必定落在三角形H1E1G1之内。

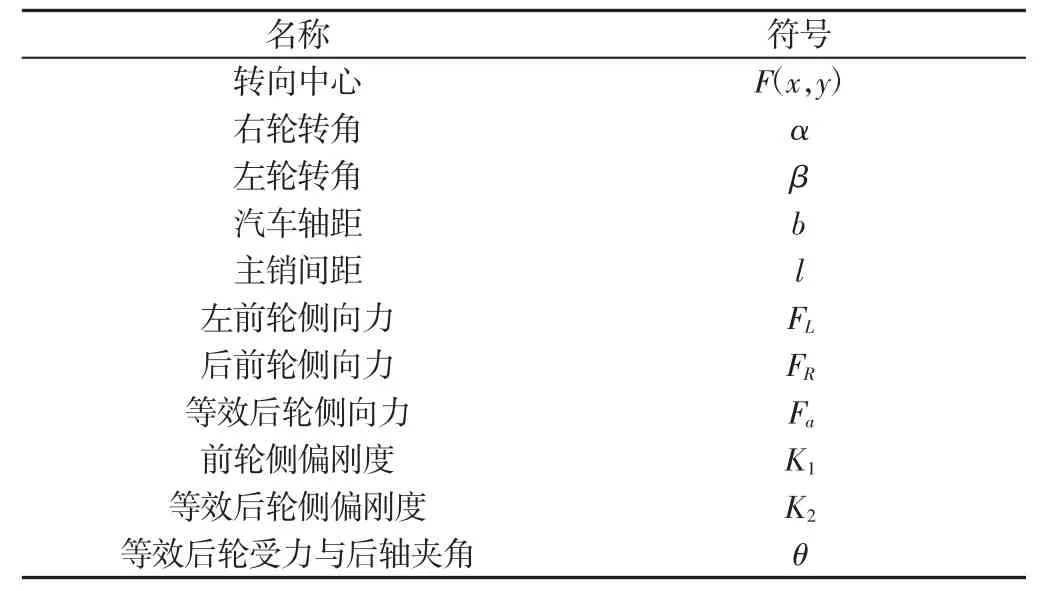
表2 后驱汽车等效三轮受力力学模型参数Tab.2 The Stressed Parameters of Rear Drive Vehicle’s Equivalent Three Wheel Model

由力和力矩的平衡、侧偏角和转向角以及汽车速度垂线的关系有：

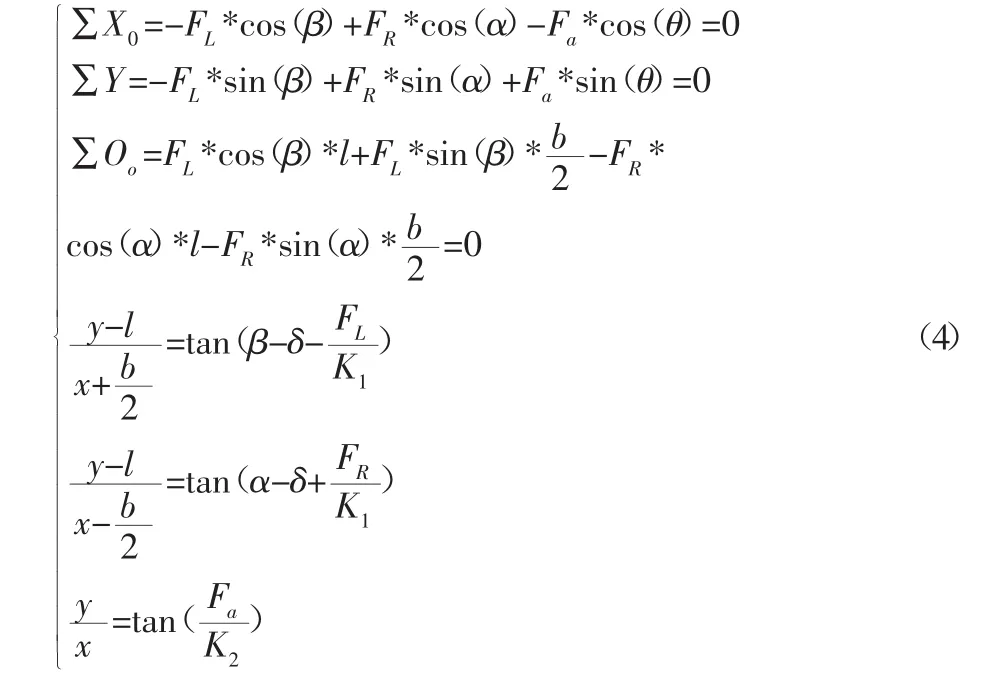
以某后驱汽车为例，车型具体参数值代入式（4）中，并用MATLAB编程对其分析求解，得到图6的各力随内轮转角关系与图7的转向中心位置关系，如表3所示。

表3 某后驱车型参数表Tab.3 A Rear Drive Vehicle’s Model Parameter Table

图6 后驱汽车等效三轮模型各力随内轮转角关系Fig.6 The Relationship of Rear Drive Vehicle’s Forces and Inner Wheel Angel in Equivalent Three Wheel Model

后驱汽车等效三轮模型左转时，左右前轮及等效后轮的侧向力都随内轮转角（左轮转角β）的增大而增大，且左前轮侧向力的变化幅度大于右前轮侧向力，这是由于后驱汽车左转向时，内轮转角大于外轮转角导致的。由前面分析可知，当内轮转角增大时，两前轮所受的侧向力增大，即前轮侧偏角增大，故前瞬心点E1和前轮中点A、B连线的延长线交后轮轴线所连的三角形H1E1G1也增大，新侧偏后的前轮瞬心点与后轮瞬心点相交时也必须侧偏得更多，即新平衡受力中各力也随着内轮转角的增大而增大，如图6所示。

在小转角时汽车的转向中心位置关系变化不怎么明显，几乎是和汽车后轴平行的一条水平直线。汽车在大转向角时，曲线变化较明显，但汽车转向中心离汽车后轴线也小于0.3×10-3m，这说明前轮添加预偏角δ后汽车在整个转向过程中转向中心都能落在汽车后轴线附近，使汽车车轮均作纯滚动运动，如图7所示。

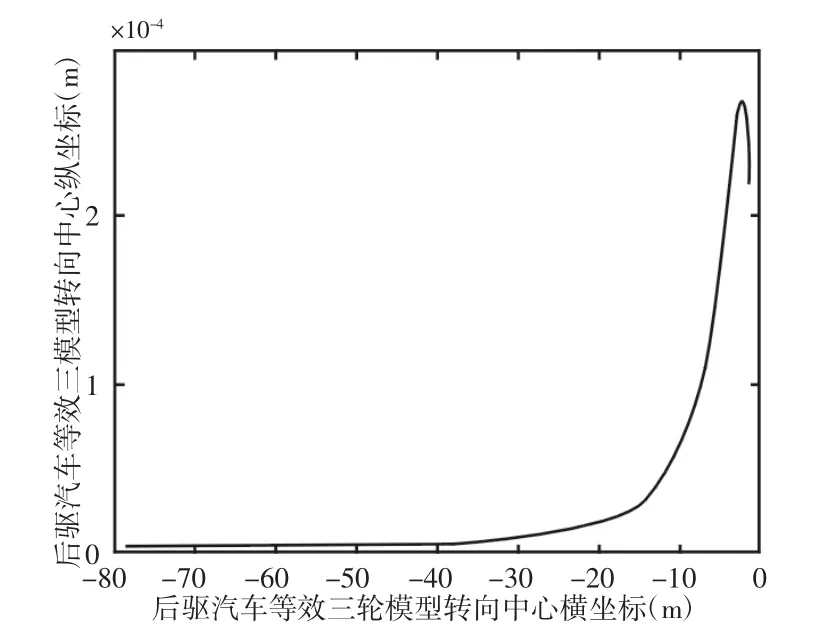
图7 后驱汽车等效三轮模型转向中心位置关系Fig.7 The Steering Center’s Position in Equivalent Three Wheel Model of Rear Drive Vehicle

同时由方程解得θ值为0，即等效后轮受力Fa的方向与后轴线时重合的。将方程组的解带入原方程组，其水平方向的合力均满足力学分析；且两前轮受力的纵向分力的合力也等于0，也说明等效后轮受力的方向θ等于0。

4.2 后驱四轮模型的建立与分析

同样以后驱汽车左转为例，建立后驱汽车四轮模型受力图，如图5（虚线）所示。图中参数，如表4所示。其中y轴为汽车左右对称线并规定向上为正方向，x轴在汽车后轴线上并规定向右为正方向。

表4 后驱汽车四轮受力力学模型参数Tab.4 The Stressed Parameters of Rear Drive Vehicle Four Wheel Model

由力平衡、力矩平衡关系以及侧偏角和转向角以及汽车速度垂线的关系有：

将表3中车型具体参数值代入式（5）中，并用MATLAB编程对其分析求解，得到四轮模型中各力随内轮转角的关系，如图8所示。

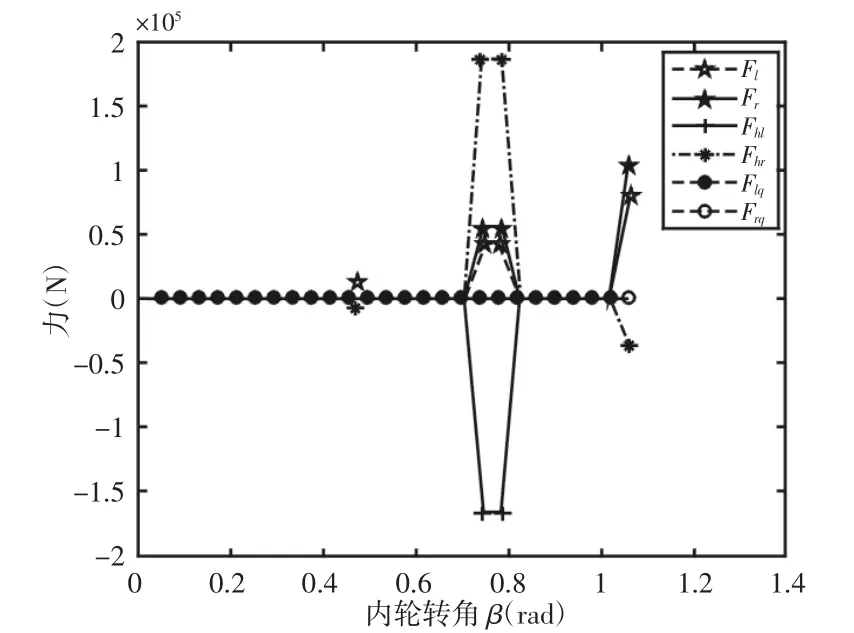
图8 各受力与内轮转角关系Fig.8 The Relationship of FL、FR、Fhl、Flq、Fhr、Frq and Inner Wheel Angel

由图8可以看到各力都有一些突变点。为了验证Matlab计算的准确性，将计算出的各力分别带入式（5）进行验证。经过验算，图8中突变点的解不满足非线性方程组，删除突变数据点后各力随内轮转角关系，如图9所示。

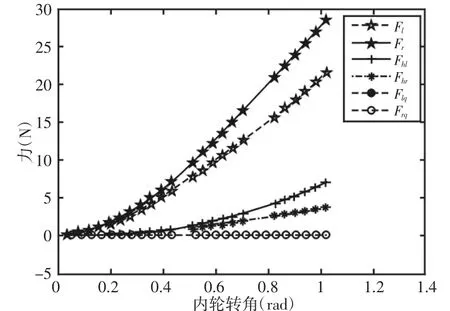
图9 后驱汽车四轮模型中各力随内轮转角关系Fig.9 The Relationship of Rear Drive Vehicle‘s Forces and Inner Wheel Angel in Four Wheel Model

由图9可知，在后驱汽车四轮模型中，左右前轮侧向力、左右后轮轴向力都随内轮转角（左轮转角β）的增大而增大，且左前轮侧向力和左后轮轴向力的变化幅度大于右前轮侧向力和右后轮轴向力，同样这也是由于后驱汽车左转向时，内轮转角大于外轮转角导致的；从图9中还看出，左右后轮纵向力不受内轮转角变化而变化。

4.3 等效三轮模型与四轮模型的对比

将四轮模型与等效三轮模型中各力与内轮转角的关系进行对比，发现四轮模型和等效三轮模型中各力的趋势和大小几乎是一样的。进一步分析得到两种模型中后驱汽车转向中心位置关系，如图10所示。

图10 后驱汽车转向中心位置关系Fig.10 The Rear Drive Vehicle Steering Center’s Position

图中10实线为后驱汽车四轮模型转向中心位置关系，虚线为等效三轮模型转向中心位关系，转向中心横坐标远离零点时转向角较小，反之转向角大。从图中可以看出，转向角较小时，等效三轮模型和四轮模型是等价的；同时，两种模型的前轮瞬心点位置纵坐标值都不大，不超过±0.3×10-3m，同样说明前轮添加预偏角δ后汽车在整个转向过程中转向中心都能落在汽车后轴线附近，使汽车车轮均作纯滚动运动。