基于ANSYS的平头塔机臂架结构静力分析
2018-12-18于洪柱
于洪柱
(山东电力建设第三工程有限公司,山东 青岛 266000)

图1 起重臂结构示意
0 引言
近年来,随着经济的发展,人工成本在逐年增加;随着施工节奏的加快,工程项目的施工周期越来越短:因此拆装更为便捷的平头塔机在市场上得到了越来越广泛的应用。平头塔机无塔帽,具有拆装速度快、主弦受力明确的优点,便于模块化设计并有利于塔群的交叉作业[1]。但是,因为起重臂省去了拉杆支撑,变成了一种悬臂受弯构件,导致起重臂质量大大增加。随着平头塔机起重量的增大,需要通过增大起重臂质量来满足结构受力要求,而起重臂质量每增加10%,平衡臂质量会增加10%,塔身质量会增加5%[2];同时,起重臂结构尺寸也会增大,导致运输超限,增加运输成本,降低经济性。因此,对起重臂结构进行优化计算,将大大提高整机的经济性。本文利用极限状态法,对平头塔机臂架结构进行简要计算。
1 臂架结构理论计算
1.1 臂架结构组成及计算载荷
本文以某款平头塔机起重臂为例进行计算,平头塔机臂架结构如图1所示,主要包括配重、起升机构、平衡臂、中心塔、起重臂、小车及吊钩滑轮组[3]。平衡臂为矩形桁架结构,起重臂为倒三角桁架结构,小车悬挂于起重臂下主弦上。起重臂和平衡臂用销轴连接于中心塔两侧。
该塔机臂架最大工作幅度为80 m,额定起重量为1 000 kN,额定起升幅度为20 m,最大幅度起重量为220 kN;平衡臂长30 m,配重为800 kN。
1.2 臂架结构计算
臂架结构平衡臂部分载荷恒定不变,均为自重载荷。起重臂各部位载荷不同,其中控制工况为额定起重量的最大工作幅度和最大幅度的最大起重量,因此本文分别对这两种工况进行分析计算。臂架结构计算中运用到的载荷主要有自重载荷、吊重载荷、风载荷和惯性载荷。根据规范载荷组合B,取各自载荷的分项系数见表1[4]。

表1 载荷分项系数
将各部分自重载荷简化为集中力作用在各自质心位置,回转惯性力和风载荷也以集中力形式作用在各自质心位置,将各载荷乘以各自分项系数,按载荷组合进行组合,可以得出不同工况下臂架结构危险截面应力,见表2。

表2 不同工况下臂架结构危险截面应力

图2 臂架结构有限元模型示意
2 有限元计算
2.1 模型建立
采用有限元分析软件ANSYS对平头塔机臂架结构进行静力计算。臂架的主要结构均为桁架结构,因此采用BEAM188单元建模。BEAM188单元适合分析细长到中等短粗的梁结构,这个单元非常适合线性、大转动和非线性大应变问题的分析。该单元完全可以满足起重臂静力分析的需要。
起重臂和平衡臂虽采用分段结构,但各段在受载过程中均不会发生移动或转动,因此各起重臂和平衡臂各节点建模时均简化为固接。各杆件均以实际截面赋予截面属性,起重臂主弦为矩形和圆管截面,平衡臂主弦为H形截面。
结构自重以惯性力的方式均匀加载在模型上,吊重、配重、各机构自重以及电气柜自重均采用集中力的方式加载在对应位置节点上。起重臂和平衡臂计算模型及加载情况如图2所示。
2.2 约束求解
将中心塔根部主弦的4个节点固定约束。将各机构自重和吊重分别乘以各自的分项系数,得出设计载荷,分别以集中力的方法施加在对应位置,惯性载荷和自重载荷以加速度方式施加。吊重按工况加在对应幅度。自重载荷因为结构部分在建模时进行了简化,模型自重小于实际自重,加载时首先计算出模型自重,再根据实际自重和模型自重的比例关系,将模型自重乘以相应系数来模拟实际自重。
2.3 计算结果
运用有限元对模型进行计算,可以得出臂架结构在不同工况下的最大应力和位移情况,如图3~图6所示。可以看出,起重臂和平衡臂最大应力均出现在根部截面,最大挠度都出现在端部,80 m幅度最大应力为473 MPa,20 m幅度最大应力为400 MPa,最大位移出现在80 m幅度吊最大载荷时,为3 700 mm。有限元计算结果和理论计算结果基本一致。起重臂采用的是高强钢,由计算可知,此结果满足设计要求。
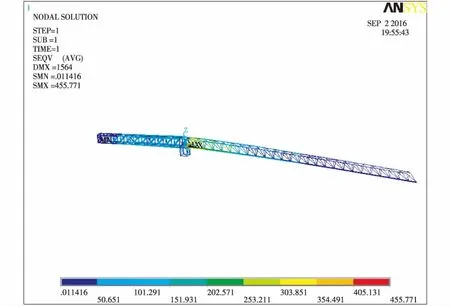
图3 20 m 100 t时臂架结构应力云图
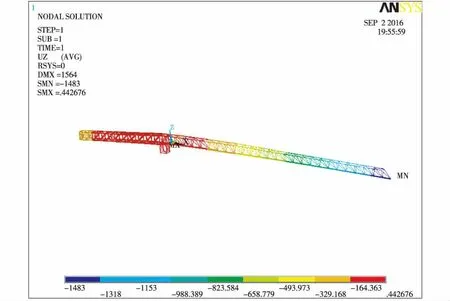
图4 20 m 100 t时臂架结构位移云图
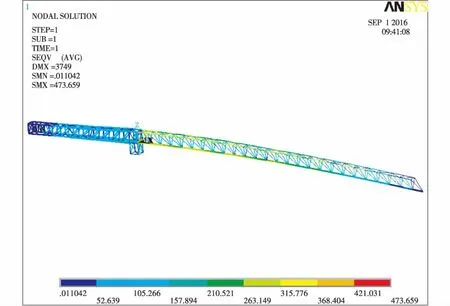
图5 80 m 22 t时臂架结构应力云图
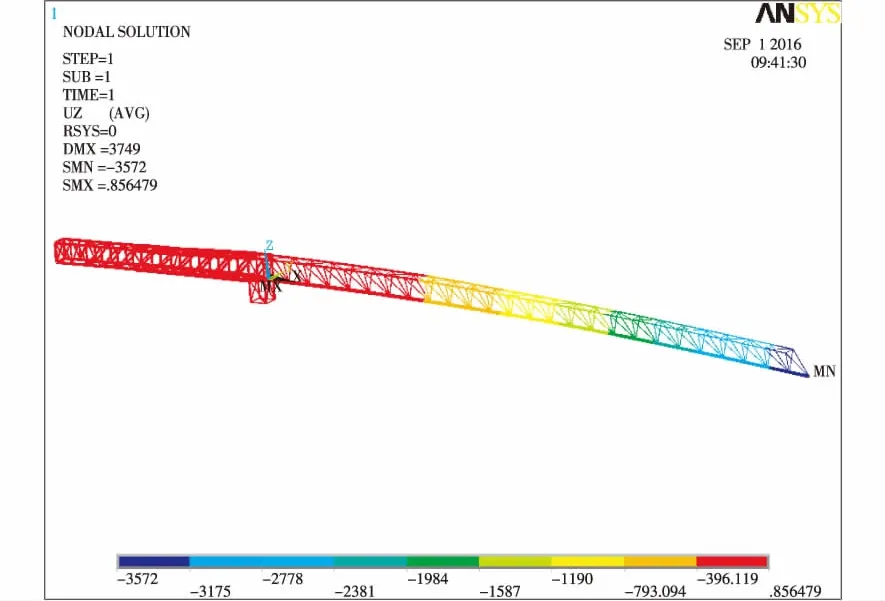
图6 80 m 22 t时臂架结构位移云图
3 结束语
本文对臂架结构分别用极限状态法理论计算和有限元进行了分析,得出了不同工况下起重臂的应力和位移分布云图。有限元计算结果和理论计算结果基本一致,验证了用极限状态法也同样可进行有限元仿真模拟,为臂架结构优化设计提供了精确依据。
