再入飞行器超高温陶瓷防热应用研究
2018-12-18李小艳曹占伟周正阳解静
李小艳,曹占伟,周正阳,解静
(1. 中国运载火箭技术研究院 研究发展中心,北京 100076;2. 空间物理重点实验室,北京 100076)
为了实现高效气动性能,新型高升阻比再入飞行器头锥一般采用尖前缘设计,在减少飞行器阻力的同时提高了飞行器操纵性能及机动性能,并且由于横向机动距离的增加也提高了其飞行安全性能。先进概念性飞行器,例如DARPA的猎鹰项目,其前缘半径尺寸在毫米的量级。对尖锥形飞行器头部驻点区域,其表面气动加热率和几何半径的平方成反比,即随着前缘采用尖细化外形减少飞行阻力的同时,其局部气动热环境变得愈发严酷,尤其在较高飞行马赫条件下,该问题更加凸显。Hyper-X超燃冲压高超声速飞行项目中,在马赫数为10的飞行条件下,气动热环境预测其前缘温度将在2400 K以上[1-2]。在这种情况下,采用 C/C材料的前缘结构即使在一次性较短的飞行中也会超过使用温度极限。针对高超声速飞行器尖前缘设计的热防护材料耐温性能一般在2000 ℃以上。
超高温陶瓷材料(Ultra High Temperature Ceramic,UHTCs)由于具有良好的耐高温性能,可以用作尖前缘设计的热防护材料,例如锆、铪化合物(HfB2的熔点温度大概在3380 ℃)。近年来在超高温陶瓷材料方面取得了很多进展。美国NASA在1997年针对 UHTCs用于飞行器尖前缘设计进行了SHARP-B1飞行试验,随后SHARP-B2飞行试验进一步证明了在极端气动加热环境下UHTCs前缘及连接结构的高效性能[3]。
UHTCs用于再入飞行器热结构设计中遇到的突出问题为高密度防热材料带来的飞行器整体质量增加[4]。材料密度是防热设计重要性能指标,HfB2材料密度为11.2 g/cm3,约为C/C类防热材料密度的6~7倍,这势必为飞行器设计带来质量增加的问题,尤其是对质量较为敏感的飞行器。由于尖前缘几何特点,其气动热环境分布随着离驻点距离的增加而迅速降低[5],其尖缘局部为峰值集中的热流分布模式,热防护设计中仅需在前缘驻点位置采用密度较高的UHTCs以承受严酷的热环境[6]。近年来,针对飞行器尖头锥设计有关学者提出了边界层防热系统概念[6],并初步对飞行器头锥的几何及材料属性进行了研究。
热约束及重量是UHTCs用于尖锥体防热设计需要折中考虑的问题。对于大钝头高超声速再入飞行器,一般采用大攻角剖面减速以满足峰值热流约束。攻角剖面是高超声速飞行器重要的热约束指标。基于UHTCs防热材料极高耐温性,表面峰值热流不再是关键热约束指标,而是关注热流沿锥体分布规律,尽可能使UHTCs仅在尖锥较小区域内使用。合理规划峰值热流水平以及热流密度分布规律与飞行攻角剖面紧密相关,而尖锥飞行器UHTCs端头质量主要由端头长度及头锥几何半径确定。实际工程设计过程中,需要探讨攻角、端头长度以及头锥半径间约束关系。
文中旨在对尖锥形飞行器UHTCs热防护系统设计要求进行研究。首先采用数值方法针对不同攻角及特性尖头锥热环境分布规律进行模拟,进一步探讨头锥外形飞行器超高温陶瓷热防护系统攻角设计约束要求,最后对基于攻角约束下尖锥形飞行器超高温陶瓷TPS热传导特性进行研究。
1 数值方法及验证
控制方程采用三维Navier Stokes方程,气体模型为处于热化学平衡状态的高温气体。采用有限体积方法进行数值求解定常层流条件下高超声速流动特性。首先采用 NASA双锥算例[7]验证当前数值模型的正确性,选取Ma为9.86,攻角为0°~16°。马赫数分布如图1所示,沿着双锥飞行器180°迎风中心线无量纲化热流分布结果如图2所示,试验数据及数值模拟结果均采用参考球头驻点 Fay-Riddle公式预测结果无量纲化。数值解与试验结果吻合很好,验证了文中方法的正确性。

图1 马赫数分布
2 尖锥热环境分布特性
采用典型尖头锥局部构型作为气动热计算物理模型。高超声速气动热环境评价除了采用飞行器表面热流密度外,还引入辐射平衡温度。表面辐射平衡温度是快速估计 TPS系统对热流响应的物理量。考虑材料本身热传导,辐射平衡温度定义为:
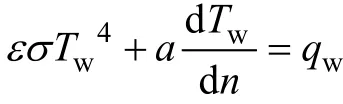
式中:qw为表面热流密度;Tw为辐射平衡温度;a为材料表面热扩散系数, a=k/(ρ c);k为材料热传导率;ρ,c分别为材料密度与热容;ε是表面辐射系数;σ为 Stefan-Boltzmann常数。当前计算中:ε=0.85,σ=5.66961×10-8Wm2/K4。

图2 无量纲化热流分布
尖锥头部半径为11 mm,锥角为12.84°,头锥体总长为2 m。计算分析选择飞行高度h=60 km,来流Ma=15。计算网格为 400万,紧邻壁面网格尺度为10-6m,保证了沿壁面y+值均小于1。计算中分析了不同攻角(0°、10°、20°)条件下头锥热环境的分布特性。
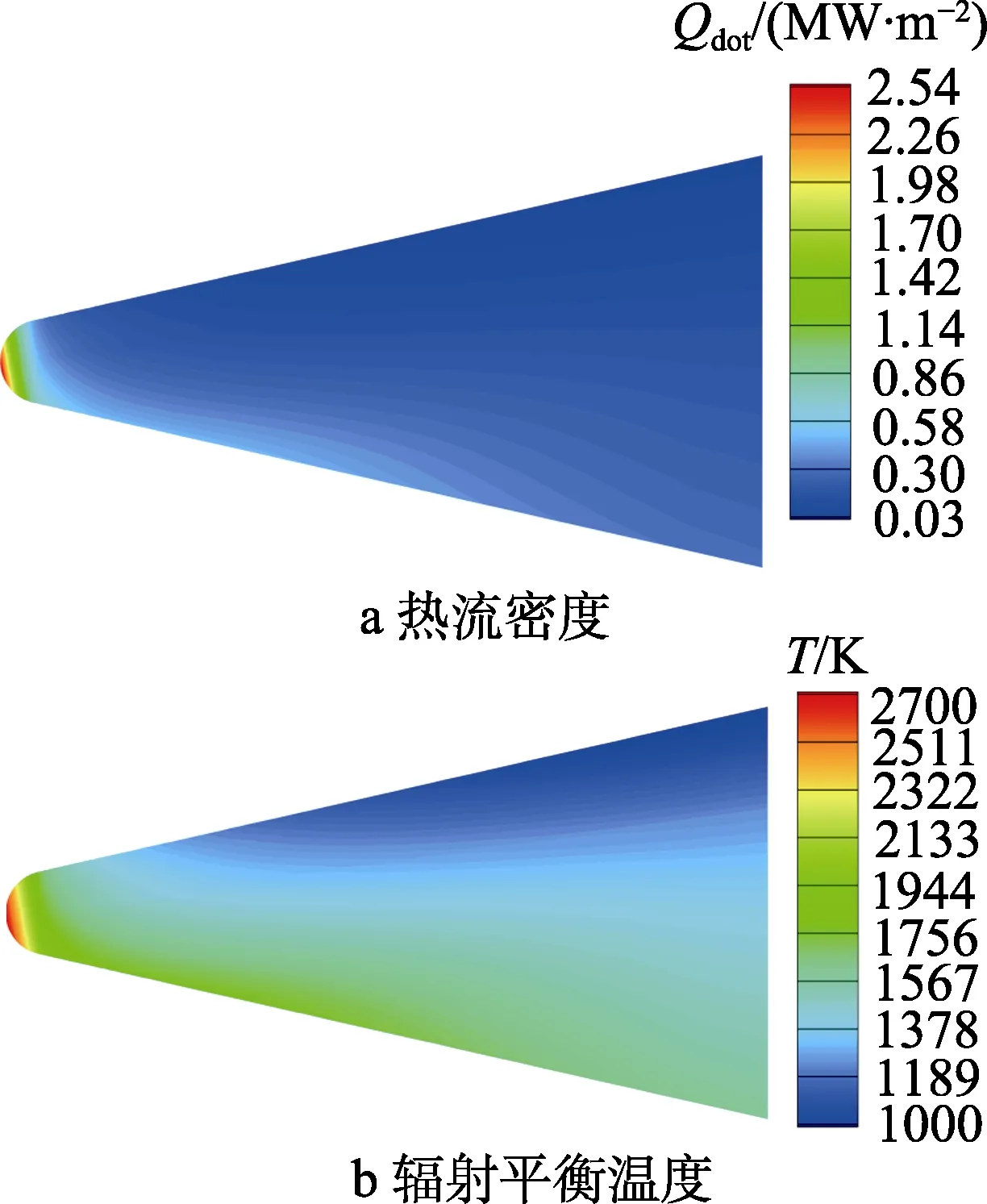
图3 热流密度与辐射平衡温度分布(攻角10°)
带攻角条件下,背风面发生分离,激波更贴近迎风面,边界层沿飞行器轴线逐渐增厚。10°下热流密度及辐射平衡温度分布如图 3所示。驻点热流为2.54 MW/m2,辐射平衡温度峰值为2700 K。对于该尖头锥,热防护系统对材料要求已经超出了抗氧化C/C或SiC材料所能达到的温度极限(1900 K)。
3 UHTCs防热约束/攻角关联性
迎风面与背风面热流及辐射平衡温度分布如图4所示。图 4中 0°攻角以上符号代表迎风面结果,0°攻角以下符号代表背风面结果。0°攻角,迎风面与背风面中心线热环境分布相同,大部分区域热流密度为0.3 MW/m2,相应的辐射平衡温度为1500 K;10°攻角,迎风面与背风面中心线热环境分布差异较大,迎风面及背风面大部分区域热流密度分别为 0.5、0.05 MW/m2,相应的辐射平衡温度分别为 1700、1100 K;20°攻角,迎风面与背风面中心线热环境分布差异进一步加大,迎风面及背风面大部分区域热流密度分别为0.7、0.05 MW/m2,相应的辐射平衡温度分别为1900、900 K。首先,通过不同攻角条件下热环境分布可以看出,高热流及辐射平衡温度仅限于驻点附近很小的区域;其次,可以发现迎风面热流及辐射平衡温度随着攻角增大迅速提高。即在定常驻点温度轨迹中,仅是攻角的变化就可以使尖锥体飞行器表面温度呈现显著差异。

图4 迎风面及背风面中心线热流密度及辐射平衡温度分布
不同攻角条件下热流密度及辐射平衡温度沿轴向剖面分布如图 5—7所示。对于 0°攻角,沿轴线热流密度及辐射平衡温度均降低,热流密度从0.24 MW/m2降到 0.18 MW/m2,辐射平衡温度从1480 K降到1390 K,且迎风面与背风面热环境分布一致。较大攻角条件下热环境分布规律明显区别于0°攻角结果,轴向截面热环境分布剖面变得更宽,随着攻角增大迎风面热环境变得更加严酷,背风面热环境则趋于缓和。例如,对于 x=0.15 m剖面位置,0°攻角条件下辐射平衡温度峰值为1370 K,而20°攻角条件下则增为1800 K。
对于UHTCs热防护设计,由于其材料良好的耐高温性能,UHTCs局部峰值热流本身在防热设计中的约束不再是主要因素,应该侧重UHTCs端头连接结构的热约束要求。随着攻角的增大,头锥末端辐射平衡温度的增加可能超过连结结构的温度使用极限,这是在 TPS设计中必须要考虑的因素。考虑到飞行器质量是一个严格的限制指标,一般 TPS设计时会在UHTCs结构末端连接密度较低、耐温性相对低的连接结构。对于当前的飞行器尖头锥,如果设定连接结构的温度限为1500 K,则该TPS设计存在极大风险。为了使整个头锥 TPS设计在安全的热约束限定边界内,飞行器需采用较小的攻角剖面,这样可以使连接结构位于安全允许温度限内。

图5 0°攻角下热流密度及辐射平衡温度沿不同轴向剖面的分布
4 UHTCs防热约束分析
通过上述分析可以发现,攻角对尖锥体头锥热环境分布影响很大。为了采用特定的 TPS设计方案,飞行器沿弹道攻角能够通过降低其他性能指标单独进行优化,如横向机动距离[10]。当飞行器再入高度-速度曲线初步确定后,确定UHTCs材料使用温度限定,头锥驻点半径可以进行优化设计,以满足防热要求。对于较小攻角范围的再入轨道,温度峰值仅仅依赖于飞行条件及驻点半径值。对于大攻角再入情况,攻角随轨道变化很大,头锥表面温度随攻角变化也变化显著。攻角越高,头锥末端即连接结构的温度也相应增高。目前,设定连接结构的温度使用极限为1900 K,为了保证连接结构在整个再入轨道范围内均在允许的温度界线内,需要设计攻角的允许范围。

图6 10°攻角下热流密度及辐射平衡温度沿不同轴向剖面的分布
设计典型尖锥外形飞行器,尖锥头部半径为72 mm,半锥角为 12.84°,整个 UHTCs端头设计长度小于0.4 m。飞行轨道采用航天飞机STS 5-BET轨道[11]。
4.1 球头半径影响
首先对头锥半径限制进行分析。设计的球头半径为0.072 m,同时选取0.03、0.04、0.05 m 等三种不同半径情况进行比较。四种不同球头半径热流密度及辐射平衡温度沿弹道分布情况如图 8所示。考虑到UHTCs使用温度限制,允许的最小球头半径为0.04 m,热流密度为3 MW/m2。对于设计头锥半径0.072 m,其热流密度峰值位于 70 km高度,峰值热流密度为2.2 MW/m2,相应的辐射平衡温度为2450 K。由于辐射平衡温度沿头锥轴线迅速降低,因此该设计UHTCs头锥均在材料的使用温度范围内。
4.2 攻角影响

图7 20°攻角下热流密度及辐射平衡温度沿不同轴向剖面的分布
通过评估UHTCs TPS连接结构的辐射平衡温度随攻角变化以实现 TPS设计攻角限定。不同头锥长度下辐射平衡温度峰值分布如图9所示。通过比较不同攻角条件下沿弹道的辐射平衡温度峰值能够限定其攻角取值。不同头锥长度下极限攻角值如图10所示。对于长度分别为0.2、0.3、0.4 m头锥,其允许的最大攻角分别为 15°、25°、35°。在目前考虑的头锥长度范围内,可以看出防热允许的最大攻角与头锥长度基本呈正比。高超声速飞行器升力大小可近似认为与攻角的余弦函数成正比,如果要实现飞行器更高升阻比要求,须飞行器攻角增大,则需要进一步加长头锥以保证TPS连接结构的安全性。
4.3 热导率影响

图8 热流密度及辐射平衡温度沿不同球头半径分布
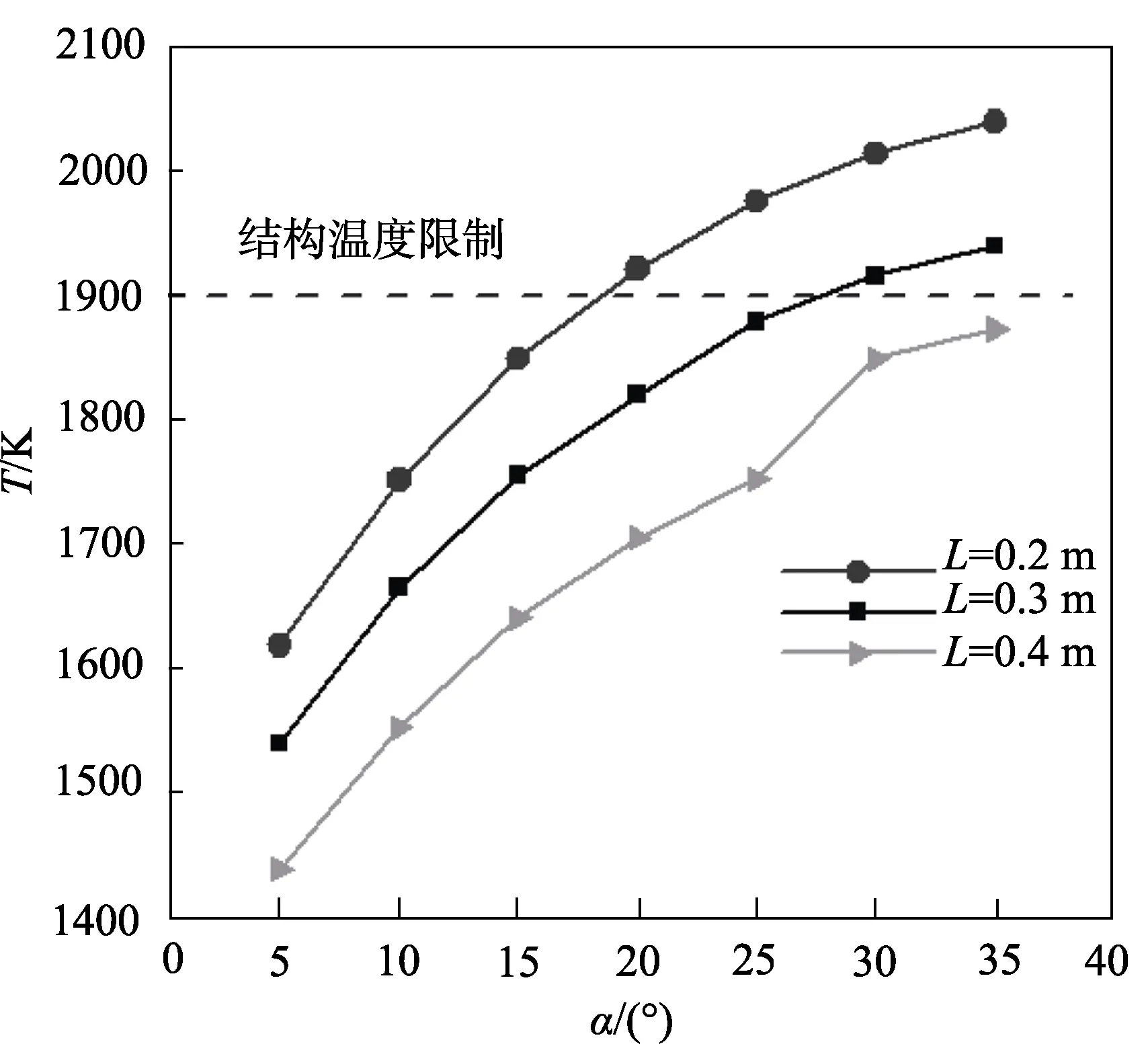
图9 不同头锥长度下辐射平衡温度峰值分布
尖头锥 TPS设计需要材料具备高热导率,来保证热流能够从驻点位置即时疏导到锥体表面以辐射到外界。对于UHTCs材料,其本身就具备优良的热传导性能。SHARP项目对各种UHTCs热导率进行了测量,其中对于HfB2/SiC材料,其热导率在2000 K时为80 W/mK。对于UHTCs类材料,由于高热导率性能其表面热传导不能忽视,气动加热表面热辐射平衡温度评估时需要考虑热流的传导及外表面辐射。为了研究热导率对UHTCs TPS设计的影响,对不同热导率UHTCs材料的导热性能进行了数值模拟研究。按照NASA标准UHTCs材料体系测量数据[9],给定UHTCs材料的密度、热容、表面辐射率,而热导率则取60 W/mK以及90 W/mK两种情况。两种UHTCs材料的各项性能参数见表1。

图10 不同头锥长度下的极限攻角αmax

表1 UHTCs性能参数
两种不同热导率UHTCs材料表面辐射平衡温度沿轴向分布如图11所示。与未考虑材料热导率影响的结果相比,表面辐射平衡温度峰值显著降低。随着热导率的增加,头锥的峰值辐射平衡温度降低205 K,而头锥末端(连接结构)的辐射平衡温度则进一步上升约50 K。因此,在UHTCs TPS设计时,为了平衡连接结构辐射平衡温度与 TPS质量的限制要求,需对材料的热导率范围进行限定。

图11 不同轴向位置辐射平衡温度分布
5 结论
文中主要对尖锥形飞行器头部表面热环境分布规律及UHTCs材料体系热防护设计进行了研究,重点研究了攻角对头锥表面热环境分布影响以及热防护设计约束要求。研究表明,尖锥飞行器高热流仅限于驻点附近很小的区域,迎风面热流随着攻角增大迅速提高;满足防热设计约束的极限飞行攻角与端头长度呈正比;超高温陶瓷热导率对端头防热设计影响较大;尖锥体超高温陶瓷端头防热设计的重要约束指标为端头连接结构温度限制,设计时需要合理优化飞行攻角剖面,选取热导率性能适中的材料。
