在运筹学教学中融入数学建模思想的应用*
2018-12-18季海波
季海波
在运筹学教学中融入数学建模思想的应用*
季海波
(宿迁学院 文理学院,江苏 宿迁 223800)
通过一个“选课策略”的案例,把数学建模的思想引入到运筹学课程教学过程中,启发学生如何利用0-1整数规划进行建模,并通过Lingo软件进行编程求解,既培养学生利用理论知识解决实际问题的能力,又提高学生的计算机应用能力。
运筹学;数学建模;Lingo软件;应用能力
1 运筹学概述
运筹学是一门以人机系统的组织、管理为对象,应用数学和计算机等工具来研究各类有限资源的合理规划使用,并提供优化决策方案的学科,是一门理论和实践应用并重的综合性学科[1]。运筹学应用范围广泛,从军事、政治到管理、经济及工程技术等许多领域都能应用到运筹学的思想和方法。运筹学和数学建模是很多高校数学与应用数学和信息与计算科学专业的核心课程。构成运筹学的理论大致分为分析理论、决策理论和随机服务理论,而运筹学主要包括的内容有线性规划、整数规划、目标规划、动态规划、图与网络分析、存储论、排队论、决策论、博弈论等。而将数学建模的思想融入到许多数学核心课程的相关研究已经有了不少的研究成果[2-4]。而对运筹学的这门课程在不同专业的教学改革研究也有了不少比较好的结果[5-8],运筹学这门课程本身绝大部分理论内容都是通过解决实际问题抽象出来的,因此在本课程的讲授过程中融入建模思想是非常合适的,而且在建模的过程中,除了介绍对应的理论方法外,还可以根据模型利用Lingo软件编程进行求解,训练学生的计算机应用能力,这样也就更加符合信科专业的培养目标——培养“应用型”人才。
2 建模思想在运筹学教学中的实际应用
本文主要通过选取一个与学生切身相关的案例“选课策略”来研究如何在运筹学教学中融入建模思想,在教学过程中既能够锻炼学生解决实际问题的能力,又能了解所需要学习的理论内容,求解过程可以融入计算机编程,锻炼学生的动手能力。以信息与计算科学专业为例,表1给出了该专业其中9门课程的具体情况。
选课要求学生至少要选两门数学课、三门运筹课和两门计算机课。
问题1:为了选择的课程门数最少,应该如何选择课程? 对于该“选课策略”问题,首先需要引导学生根据题目要求该如何假设我们的决策变量。假设决策变量的原则是,除了假设出对应的变量后,还能够较容易地利用设出来的决策变量建立出模型的目标和相应约束条件。
表1 信息与计算科学专业课程情况
课号课程名称学分所属类别先修课程 1数学分析5数学 2高等代数4数学 3最优化方法4数学、运筹数学分析、高等代数 4数据结构3数学、计算机计算机编程 5应用统计4数学、运筹数学分析、高等代数 6计算机模拟3计算机、运筹计算机编程 7计算机编程2计算机 8预测理论2运筹应用统计 9数学实验3运筹、计算机数学分析、高等代数
由于每个学生与每门课程之间只有选与不选两种情况,因此可以考虑整数规划中的0-1规划,假设决策变量为:

下一步根据问题1建立模型的目标函数,为:
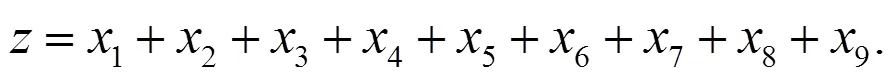
最后一步寻找约束条件,其中第一块约束条件是选择每类课程门数的要求,可得约束:

第二块约束条件是课号为3,4,5,6,8,9的这些课程有先修课程的限制,因此可以建立如下约束条件:
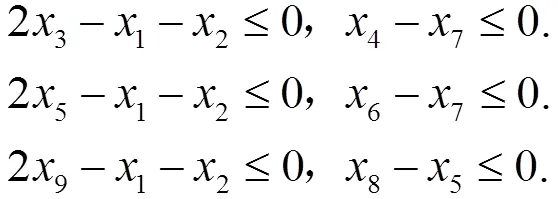
由式(1)(2)(3)就可以得到选课最少情况下的数学模型:
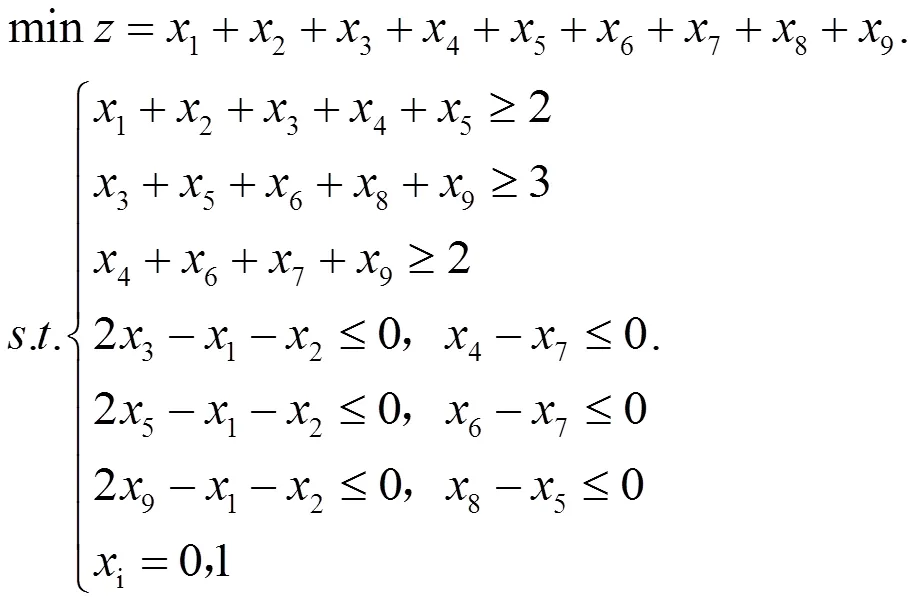
在这个过程中,学生就由数学建模的思想了解了运筹学中的0-1整数规划的模型,知道运筹学是可以解决与他们切身相关的实际问题。但是在实际选课时,虽然做到了选课门数最少,大部分高校还有学分的要求,也就是说,虽然修的课程最少,但是学分没有修够,还必须进一步选修其他课程,所以问题1的最优解在考虑学分这个方面有可能是无法应用的,那么怎么才能使得我们所得到的最优解既能满足学生需求,还能满足学校需要呢?于是在教学过程中紧跟着提出以下问题。
问题2:如果能够使得选修的课程尽可能少,学分尽可能多,那么该如何选择课程呢?
其实问题2只是在问题1的基础上增加了一个总学分的目标函数,在模型(4)的基础上增加目标:
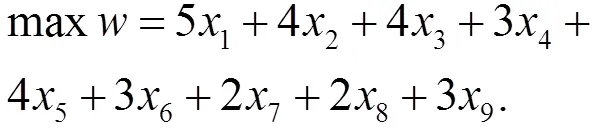
即可得到问题2数学模型:

通过上述过程,把数学建模的思想融入到了运筹学中的整数规划的教学过程中,让学生了解什么是数学建模,怎么样方便地假设出决策变量。当模型建立完以后,可以介绍一下解决一般问题的0-1整数规划的理论方法隐枚举法。该法其实是将完全穷举法进行改进,通过适当选择初值来减少穷举的过程。为了更进一步提高学生的计算机应用能力,继续指导学生利用Lingo软件进行编程来求出结果,从而验证理论方法的正确性,特别地将问题2解决方法作了调整。问题2是一个多目标规划问题,在解决问题2时需要将多目标规划改为单目标规划,主要做法是将其中一个目标函数整体取相反数,与另外一个目标相加就可以得到单目标规划问题,例如目标可以改成max-或者min-.表2是利用Lingo软件编程得到的问题1和问题2的结果。
表2 Lingo给出的选课策略
选课策略选课门数总学分 问题1数学分析、高等代数、最优化方法,计算机模拟、计算机编程、数学实验622 问题2数学分析、高等代数、最优化方法、数据结构、应用统计、计算机模拟、计算机编程、预测理论、数学实验931
3 结束语
本文主要通过运筹学中0-1整数规划的一个“选课策略”案例,融入数学建模的思想,建立了一般的0-1整数规划模型,求解方法不同于分配问题中的匈牙利法,需要用到隐枚举法才能解决。理论方法比较复杂,又借助于Lingo软件进行编程得到了对应不同情况下的选课策略,这样既让学生对理论方法有所了解,还可以提高学生的计算机软件的应用能力。在平时的运筹学课程教学过程中,运筹学的每一块教学内容都可以启发学生去寻找一些实际案例,通过案例运用运筹学中对应章节的内容进行建模,再用对应的理论算法进行求解,并通过Lingo软件进行编程求解。实践证明,教师利用这样的理念进行教学,有利于提高学生解决实际问题的能力和计算机应用能力,还可以激发学生学习数学的积极性,这样的案例教学法还可以应用到其他很多课程的教学中去。
[1]胡运权.运筹学基础及应用[M].第6版.北京:高等教育出版社,2014.
[2]李大潜.将数学建模思想融入数学主干课程[J].中国大学数学,2006,22(1):3-7.
[3]田宝单,姚许乾,陈宁.数学建模思想在常微分方程教学中的应用[J].高师理科学刊,2017,37(6):67-69.
[4]谭永基.将数学建模思想融入通识教育数学核心课程[J].高等数学研究,2009,12(2):8-12.
[5]苏红畏.二本院校的《运筹学》课程教学改革研究[J].教育教学论坛,2013(21):48-50.
[6]陈娜.二本院校数学类专业运筹学课程教学改革探索[J].当代教育理论与实践,2015,7(6):56-58.
[7]杨茂盛,孔凡楼,张炜.以科研促进运筹学教学改革与探索[J].西安建筑科技大学学报(社会科学版),2006,25(6):52-54.
[8]胡胜发,刘桂真.国家精品课程运筹学的教学改革与实践[J].中国大学教学,2006(7):9-10.
季海波(1981—),男,江苏南通人,硕士,讲师,研究方向为极限理论。
2017年江苏省高等教育教改研究项目(2017JSJG278);宿迁学院教改项目(sqc2018jg06)
2095-6835(2018)23-0134-02
O13;G642.0
A
10.15913/j.cnki.kjycx.2018.23.134
〔编辑:王霞〕
