约束回归分析方法在地应力场模拟中的应用
2018-12-18鲁立志杨树新姚瑞郭啟良
鲁立志,杨树新,姚瑞,郭啟良
约束回归分析方法在地应力场模拟中的应用
鲁立志,杨树新,姚瑞,郭啟良
(中国地震局地壳应力研究所,北京 100085)
建立了三维有限元模型,采用约束回归分析方法,对实际地应力场进行评估,使模拟结果更接近实际地应力场,为岩土工程地应力评估研究提供了一种有效方法。
有限元;回归分析;岩土工程;地应力
1 引言
工程区发生的地质灾害与工程区的地应力环境密切相关,准确了解工程区所处的地应力场状态,对于工程设计、施工、生产具有十分重要的科学意义与实用价值。
以往许多学者从不同角度,比如构造演变历史、地壳变形、震源机制等方面探讨和论述了现今构造应力特征,做了许多有益的工作[1-3]。但以上方法只能给出一个地点或地区主应力大致方位,不能给出绝对应力值的大小。通常要了解现今地应力状态,主要通过原地应力测量数据获得,但受测量条件限制只能在工程区进行少量的实测工作。
有限元方法是一种数值计算方法,利用三维有限元模型,可应用于岩土工程中评估地应力场分布情况。然而,地应力场受多种因素相互作用影响,较为复杂。20世纪60年代基本是采用实测点应力结果综合评定,对应力场进行半定量描述[4];20世纪70年代以来,各领域许多学者探讨了用有限元等数值模拟方法研究地壳应力场,逐步将回归分析与数值模拟分析结果相结合,形成把实测点应力转化为场应力的分析方法。本文结合实际地应力测量数据,采用有约束的回归分析方法对原地应力进行有限元模拟,为岩土工程地应力评估研究提供一种有效方法。
2 约束回归分析方法简述
2.1 研究的技术思路
构造应力场的形成决定于重力场作用、地质构造作用和岩土介质等众多因素,通过回归实际的地应力场可以确定诸多因素的合理量值。根据地形地貌资料和地质勘测资料建立三维有限元模型,并选取构造运动、重力场等主要影响因素作为待定的变量,拟定初始载荷边界条件分别加载到有限元模型中计算,建立应力实测数据与待定因素之间的多元回归方程;然后用逐步回归分析考察待定因素的全面性及显著性,通过约束条件的回归分析确定各待定因素的最终值,使其更合理、可靠;最后将各待定因素拟定的初始载荷乘以所求得的对应系数同时加载到模型中进行应力场模拟计算,从而得到更符合实测数据的地应力场[5-6]。
2.2 有约束的回归分析模型
在构成实际地应力的因素中有些待定因素的某些性质是已知的,比如岩体比例、区域构造主应力的概略方向等,为充分利用已知资料,使回归分析结果更合理可靠,应该依据已知资料进行约束。本文采用的线性约束数学模型[7]如下:

式(1)中:n为单位矩阵。
其中的,,,,,如下:
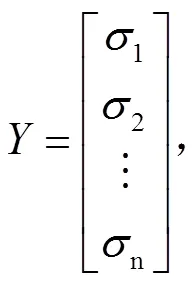
(2)
式(2)中:i(=1,2,…,)为实测应力值;i,j(=1,2,…,;=1,2,…,)为个拟选待定因素作用下的模拟计算值。0,1,2,…,m为待定参数;为随机误差,并假定其数学期望和均方差分别为()= 0,() =2.

式(3)中:ij,i(=1,2,…,;=1,2,…,)分别为为线形约束系数;i为常数项。
根据微积分中求条件极值理论,用拉格朗日乘子法求线性约束回归方程残差平方和的最小值解,回归方程的显著性检验采用F检验。
3 工程案例
3.1 计算模型的建立
本文选取以某工程区地下厂房群为中心,东西向长约5 000 m,南北宽约4 500 m,向下取到800 m高程作为模型截取范围。
有限元坐标系轴取北偏东60°方向,轴取北偏西30°方向,轴垂直于地面,计算中考虑了地形地貌,建立三维有限元模型如图1所示,考虑工程区风化岩体、断层的介质力学参数如表1所示。

图1 三维有限元模型网格图
表1 介质力学参数表
材料介质弹性模量/MPa泊松比容重/(T/M3) 微风化岩体16 000.00.242.75 弱、强风化岩体6 0000.262.74 断层F2 000.00.352.67
3.2 待回归因素的分析与模拟
据地质构造分析和原地应力测量资料(如表2所示)的综合分析结果,最大主压应力方向为向。
考虑地球托举约束模型底部向位移,模型东与北侧约束,方向位移。
考虑岩体受重力作用(如图2所示)和在西、南侧受到水平地质构造挤压作用1,2(如图3所示),选取,1,2作为待回归因素。
表2 地应力实测结果
测zn点水平主应力三维主应力 名称量值/MPasH方位/°名称量值/MPa方位/°倾角/° CFZK1sH7.74317~321s18.3731926 sh5.09s25.1419350 s35.076428 CFZK2sH//s17.88161.6﹣3.37 s h/s27.1855.51﹣77.96 s34.73252.2﹣11.55 CFZK3sH12.65325~335s19.6033619 sh7.48s25.3916571 s33.93673 CFZK4sH6.40328~355s16.413408 sh4.74s25.9723561 s34.407428
注:表2中,H为水平最大主应力;h为水平最小主应力;1,2,3分别是最大、中间、最小主应力。
3.3 回归分析
3.3.1 回归方程
设共有个观测值数据值,用k(=1,…,)表示。将图2和图3模式中3个待定因素,1,2分别加载到有限元模型中,求得各个测点有限元模拟观测值分别为krh,KP1,KP2.
krh,KP1,KP2的基本方程如下:
k=rhkrh+p1KP1+p2KP2+k. (4)
式(4)中:rh为重力因素的待回归系数;p1,p2分别为构造因素1,2的待回归系数;k为误差估值。
3.3.2 回归计算
在计算中使用了4个钻孔的实测数据,其有限元坐标系下的应力分量如表3所示。按图2和图3所示模式计算出的有限元模拟值如表3所示。
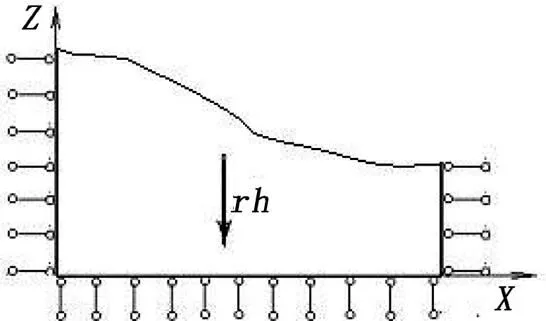
图2 重力作用模式

图3 构造作用模式
表3 回归分析数据表
测点编号应力分量实测应力有限元模拟值回归应力 σkp1/MPaσkp2/MPaσkrh/MPa CFZK1σx5.193.470.833.624.430.76 σy7.640.982.82.017.140.51 σz5.750.58﹣0.225.234.741.01 τxy﹣0.50.040.070.10.3﹣0.8 τyz1.260.03﹣0.46﹣0.25﹣1.12.36 τzx﹣0.28﹣1.39﹣0.25﹣1.75﹣1.771.49 CFZK2σx4.953.350.893.754.620.33 σy7.750.9732.317.690.06 σz7.080.29﹣0.36.746.10.98 τxy0.620.010.090.010.190.43 τyz0.140.04﹣0.3﹣0.04﹣0.630.77 τzx﹣0.46﹣1.08﹣0.26﹣1.62﹣1.81.34 CFZK3σx3.993.490.963.774.74﹣0.75 σy9.111.053.082.27.811.3 σz5.820.48﹣0.245.414.920.9 τxy0.540.050.140.120.420.12 τyz1.270.06﹣0.39﹣0.08﹣0.812.08 τzx0.05﹣1.25﹣0.26﹣1.62﹣1.71.75 CFZK4σx4.923.40.833.64.430.48 σy6.310.962.832.067.28﹣0.97 σz5.510.45﹣0.265.735.170.34 τxy0.110.050.060.080.24﹣0.13 τyz0.040.02﹣0.42﹣0.23﹣1.011.05 τzx﹣0.36﹣1.31﹣0.26﹣1.77﹣1.851.5
3.3.2.1 逐步回归分析计算
通过对重力因素和构造因素1,2逐步回归计算,得到重力回归系数rh= 0.970 9,地质构造回归系数p1= ﹣0.400 5,p2=1.677 8,常数项0= 0.302,复相关系数=0.973 3,回归方程显著性检验值=119.866 6.
从逐步回归分析结果来看,重力因素系数rh=0.970 9,与实际的重力因素大小接近。回归方程复相关系数= 0.973 3与临界值0.05=0.388相比,前者明显较大;显著性检验=119.866 6与临界值0.05=3.01相比,前者明显较大,说明回归效果显著。同时,本文考虑的三个回归待选因素与工程区构造地质背景相符,说明此三个回归待选因素是形成该地区地应力主要因素。
3.3.2.2 约束回归分析计算及结果
由逐步回归分析确定的三个因素,1,2是计算该工程区应力场主要控制因素,可忽略其他因素,因此0=0.0,又因工程区岩体的比重取值比较合理可靠,自重因素对应力场的影响是确定的,因此rh=1.0.
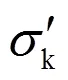
4 结论
本文应用约束回归数理统计方法研究地应力场模拟,使分析结果更合理、更准确。对某工程区地应力场进行数值模拟,计算结果表明,采用约束回归分析方法对实际地应力场进行评估,得到的分析结果更接近实际地应力场。
[1]马杏垣.中国岩石圈动力学地图集[M].北京:中国地图出版社,1989.
[2]谢富仁,崔效锋,赵建涛,等.中国大陆及邻区现代构造应力场分区[J].地球物理学报,2004(4):654-662.
[3]杨树新,陈连旺,谢富仁.中国大陆现今构造应力场的回归分析研究[J].岩土力学,2003(Suppl 2):357-360.
[4]Hast N.The state of stress in the upper of the Earth’s crust[J]. Tectonophysics,1969(8):169-211.
[5]姚瑞,杨树新,周俊,等.某水电站地应力场数值模拟与工程区稳定性分析[J].地震工程与工程振动,2011,31(2):103-110.
[6]王迪,姚瑞,杨树新,等.新疆某水电站地应力场数值模拟与分析[J].地壳构造与地壳应力文集,2016(1):65-77.
[7]方开泰.实用回归分析[M].北京:科学出版社,1989.
2095-6835(2018)23-0053-03
P553
A
10.15913/j.cnki.kjycx.2018.23.053
鲁立志(1989—),男,硕士,主要从事地应力场数值模拟及地球动力学研究工作。
姚瑞(1985—),女,硕士,助理研究员,主要从事地应力数据应用与构造应力场数值模拟工作。
〔编辑:严丽琴〕
