基于高频注入法的无轴承异步电机转子位移观测*

张晓峰，卜文绍，陈有鹏

(1.河南科技大学 信息工程学院，河南 洛阳 471023； 2.河南科技大学 电气工程学院，河南 洛阳 471023)

0 引 言

无轴承电机是根据磁悬浮轴承与普通交流电机定子结构的相似性，提出的一种适合于高速旋转的新型电机。在无轴承电机的定子槽中嵌放有两套绕组，即转矩绕组和悬浮绕组。通过两套绕组所产生的气隙磁场的叠加，可使电机部分气隙区域的磁场增强，部分气隙区域的磁场减弱，可产生作用与转子的径向磁悬浮力[1]。无轴承控制技术可用于各种交流电机，因无轴承异步电机具有健壮紧凑的结构，已成为国内外研究的热点之一。要实现无轴承异步电机转子的稳定悬浮运行，需要对转子径向位移进行实时检测和反馈。采用位移传感器检测转子径向位移会增加系统成本，而且存在安装困难。因此，开展研究无轴承异步电机转子径向位移的自传感检测技术研究，具有重要理论和实际意义。

关于无轴承电机的无位移传感器研究，国内外已取得可喜的研究进展。目前实现无轴承电机转子位移自检测的方法主要有三种：基于人工智能的方法[1-3]；高频注入法[4-8]；观测器法[9]。文献[1]采用最小二乘支持向量机进行转子位移估计；文献[4]分析了转矩绕组和悬浮绕组之间的互感与转子径向位移成线性关系的特点，通过在转矩绕组注入高频信号，提取悬浮绕组差分电压信号来检测转子位移；文献[5]利用悬浮绕组自感，通过在悬浮绕组中注入高频信号，提取悬浮绕组的差分电压信号来实现转子位移自检测；为了提高高频信号注入法对位移的估算精度，文献[7]使用最小二乘法对永磁无轴承电机转矩绕组电感、悬浮绕组电感，以及两套绕组之间的互感参数进行了辨识研究；文献[8]分析了基于两套绕组互感的高频信号注入法位移检测机理，设计了位移检测电路，但未对无位移传感器控制系统进行深入研究；文献[9]根据主动磁轴承的数学模型，通过建立位移观测器，实现了转子位移自检测。但观测器法需要精确的无轴承电机数学模型，鲁棒性差。文献[10]利用转子偏心引起的磁链差，通过悬浮绕组电压、电流对磁链进行辨识，从而推算出转子位移。

目前，高频信号注入法在普通交流电机无速度传感器控制中已有较多应用；在无轴承电机无位移传感器方面亦有报道，在所采用的数学模型和提取信号方法方面有所不同。文章在无轴承异步电机逆系统解耦控制基础上，利用转矩绕组和悬浮绕组之间的互感变化规律，在转矩绕组注入高频电压信号，通过提取悬浮绕组高频电流信号，进而实现对径向位移的估算。

1 基于高频信号注入法的位移估计原理

1.1 基本原理

根据无轴承异步电机的电感矩阵方程[11]，可得到在两相同步旋转d-q坐标系下的磁链方程：

(1)

式中ψ4d、ψ4q和ψ2d、ψ2q分别为转矩绕组和悬浮绕组沿d、q轴的磁链分量；L4、L2分别为转矩绕组和悬浮绕组自电感；α、β为α-β静止坐标系中的转子径向位移分量；is4d、is4q和is2d、is2q分别为转矩绕组和悬浮绕组沿d、q轴的电流分量；M为两套定子绕组之间的互感系数。

忽略绕组电阻压降，由式(1)可得d-q坐标系下的无轴承异步电机电压方程：

(2)

式中u4d、u4q、u2d、u2q分别转矩绕组和悬浮绕组电压分量；p为微分算子。

对式(2)求反变换，忽略位移平方项并作近似处理，可得无轴承异步电机电流方程：

(3)

根据式(3)，因为转矩绕组和悬浮绕组之间存在互感，当给转矩绕组注入高频电压信号时，可在悬浮绕组中检测出含有径向位移信息的高频互感电流信号。

沿d轴给转矩绕组注入脉振高频电压信号，即：

U4d-i=Uisin(ωit),U4q-i=0

(4)

式中U4d-i和U4q-i分别为转矩绕组d轴和q轴注入的高频电压信号；Ui为高频电压幅值。

将式(4)代入式(3)，可得悬浮绕组高频电流方程：

(5)

对式(5)两边取积分，可得悬浮绕组高频感应电流与转子径向位移之间的关系式：

(6)

由式(6)看出：悬浮绕组d、q轴高频电流分量is2d-i、is2q-i包含有互相解耦的转子径向位移量α和β。用电流传感器检测到悬浮绕组电流，通过合适的信号解调技术即可得到转子径向位移信号。

1.2 转子径向位移信号的估算

通过式(6)得到转子径向位移，需对实测悬浮绕组电流信号进行解调。具体步骤为：

Step1：通过带通滤波器(BPF)从悬浮绕组电流中提取出高频感应电流分量。

Step2：将注入到转矩绕组的高频电压信号经移相器分别移相90°和-90°后，与Step1中得到的悬浮绕组高频感应电流信号一起送进乘法解调器进行解调。即将式(6)分别乘以cos(ωit)和-cos(ωit)，得：

(7)

Step3：将Step2得到的电流信号经过低通滤波器(LPF)滤除高频分量，得到直流信号分量：

(8)

式中 转子径向位移α、β与相应的直流分量成线性关系，据此可以得到转子径向位移量。

图1是转子径向位移估算器结构图。如图1所示。首先将测得的悬浮绕组电流经带通滤波器提取出高频感应电流信号；然后经移相器和乘法器进行解调；最后通过低通滤波器，得到包含转子径向位移信息的直流信号。

图1 径向位移估算器结构图Fig.1 Structure diagram of radial displacement estimator

2 无位移传感器控制系统仿真分析

2.1 无位移传感器控制系统结构

无轴承异步电机的可控径向力模型为：

(9)

式中的Km是与电机结构有关的系数，其表达式为：

(10)

式(9)～式(10)中Fα、Fβ分别为可控悬浮力沿α-β坐标轴分量；μ0为气隙磁导率；l为电机定子铁心长度；r为定子内径；Lm2为悬浮绕组单相激磁电感；N1、N2分别为转矩绕组、悬浮绕组的有效串联匝数。ψ4d、ψ4q分别为d-q坐标系转矩系统气隙磁链分量，可由气隙磁链和转子磁链之间的关系得到：

(11)

式中ψr为转矩系统的转子磁链；Lm、Lr、Lr1l分别为定转子互感、转子自感、转子漏感。

图2所示为无轴承异步电机无位移传感器控制系统结构，包括四极转矩控制系统和两极悬浮控制系统。在转矩控制系统中，为实现转速和磁链解耦控制，采用逆系统方法实现解耦控制[12]，具体设计方法此处不再详述。转矩逆系统的输出变量为d-q坐标系下的定子电压，在d轴注入高频正弦电压信号。在悬浮控制系统中，根据第1.2节所述的方法，提取转子的径向位移信号，将位移估计值用于位移闭环反馈信号，从而实现无轴承异步电机无位移传感器控制。

2.2 系统仿真验证与分析

在图2所示控制系统结构的基础上，通过MATLAB/SIMULINK仿真实验来验证此方法的正确性。仿真实验所用样机的参数见表1。

表1 无轴承异步电机样机参数Tab.1 Prototype parameters of bearingless induction motors

仿真条件设置如下：磁链给定0.6 Wb，转速给定1 500 r/min，在t=1 s时，转速突变到3 000 r/min，径向位移给定α=0 mm、β=0 mm；初始径向位移α0=-0.13 mm、β0=-0.14 mm。图3～图6给出了系统仿真响应结果，其中：图3给出了电机启动至稳定运行时的转速响应曲线；图4、图5分别为电机α轴方向和β轴方向转子实际位移和估算位移曲线。为便于观察对比分析，图6给出了采用高频信号注入法估算的位移和实际位移误差曲线。

图2 无轴承异步电机无位移传感器控制系统结构框图Fig.2 Structural block diagram of sensorless control system for bearingless induction motor

图3 转速响应曲线Fig.3 Response curve of speed

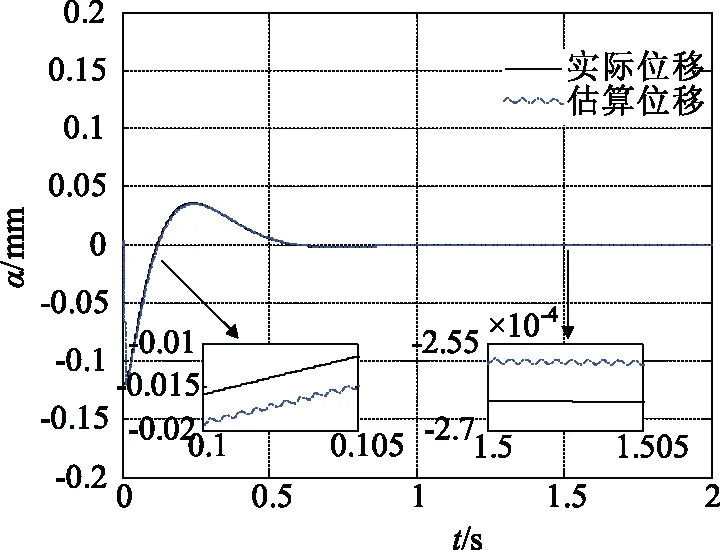
图4 α方向位移响应曲线Fig.4 Response curve of α displacement

从图3～图6可以看出：

(1)起动过程中，转速出现了超调，超调量约为40 r/min，但在0.15 s内稳定运行在给定的1 500 r/min；

(2)电机在起浮阶段，转子的α和β轴方向位移都略有超调，但超调量均小于辅助轴承间隙0.2 mm。此结果表明：采用高频信号注入法时，可以确保电机从静止到给定转速的稳定磁悬浮运行控制;

图5 β方向位移响应曲线Fig.5 Response curve of β displacement

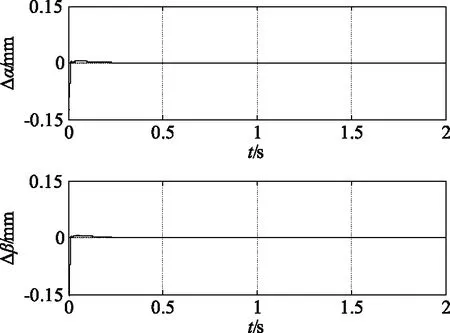
图6 位移估算误差曲线Fig.6 Displacement estimation error curve

(3)电机启动瞬间，α轴和β轴方向估算的位移偏差较大；当电机稳定运行时，误差几乎为0。从图4、图5中的局部放大图可以更加精确地看出，高频信号注入法估算的位移略小于实际位移。这是由于在高频信号注入法中，滤波器的加入给系统带来了时间延迟，使得估算的位移滞后实际位移。但是，此误差数量级很小，对无轴承异步电机控制系统控制性能的影响可以忽略不计；

(4)从图4、图5中的局部放大图可以看出，在稳定悬浮运行阶段，α方向和β方向估算位移有周期性高频脉动，位移的微量脉动源于PWM高频调制，但波动幅度均小于10-5mm，可以忽略不计。

为进一步验证所设计的无位移传感器控制系统的动态性能，当电机以额定转速1 500 r/min稳定运行时，α轴给定位移信号在时间t=1.5 s时突变到-0.03 mm，t=2.5 s时恢复到0 mm。β轴给定径向位移信号在时间t=3.5 s时突变到0.03 mm，t=4.5 s时恢复到0 mm。图7、图8分别为位移突变时转子α方向和β方向的位移曲线。从图7、图8可以看出：

(1)当α轴和β轴径向位移发生突变时，α轴和β轴估算径向位移与实际位移波形基本上保持一致，表明高频信号注入法能够精确地对转子位移进行在线估算，并且响应时间快，满足控制系统性能；

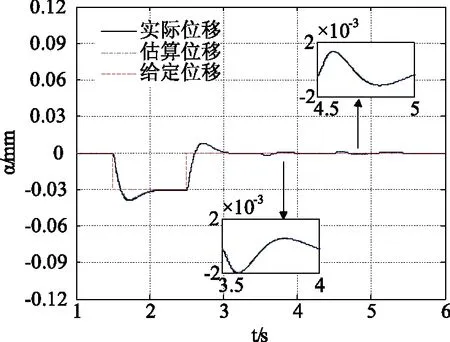
图7 位移突变时α方向位移曲线Fig.7 α displacement curve of displacement mutation

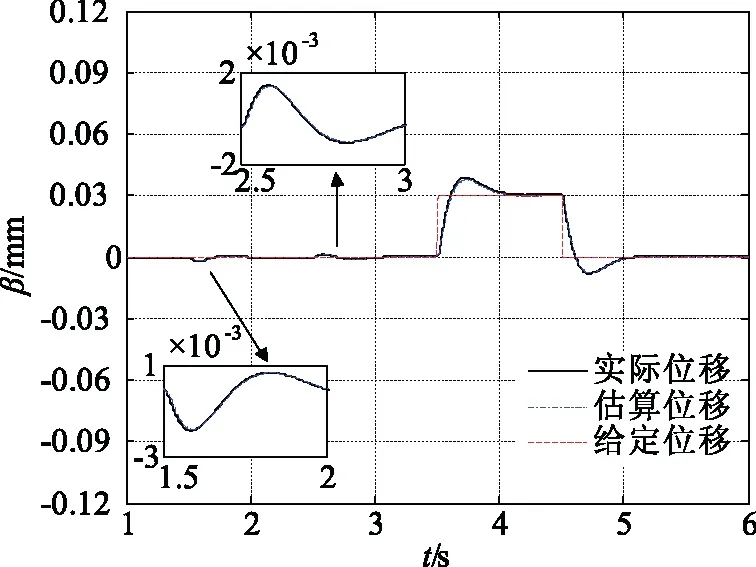
图8 位移突变时β方向位移曲线Fig.8 β displacement curve of displacement mutation

(2)当α向位移t=1.5 s和t=2.5 s时刻发生突变时，β方向位移波动幅度小于0.004 mm，所受影响很小，表明α方向和β方向位移分量之间实现了良好的动态解耦。

3 结束语

为了解决无轴承异步电机中机械式位移传感器安装困难、成本增加等问题，根据转矩绕组与悬浮绕组之间的互感耦合特性，研究了基于高频信号注入法的转子径向位移估算方法。首先在转矩绕组注入高频电压信号；然后通过检测提取悬浮绕组中的高频互感电流信号，用以估算转子径向位移，进而设计出转子径向位移估算器。控制系统仿真结果表明：采用文中所提出的方法，可以较高的精度估算出转子径向位移信号，并且能实现无轴承异步电机的无位移传感器系统稳定悬浮运行控制。另外，相比人工智能方法和观测器法，基于高频信号注入法进行转子位移观测，具有对电机参数变化不敏感的特点。