二维圆柱形亚波长结构集成芯片的设计方法

王加科，张雷梦婷 ，郑阳，何峰，邱伟

（1.长春理工大学 光电工程学院，长春 130022；2.长春理工大学 光电测控与光信息传输技术教育部重点实验室，长春 130022；3.上海航天控制技术研究所，上海 201109）

衍射透镜与谐衍射透镜设计和制作方法已经很成熟，通过台阶的高低实现相位差，从而达到调制波前相位的目的[1]。衍射透镜可以用传统套刻法和激光直写的方法制作而成，而多次刻蚀导致多台阶式衍射元件加工精度大大降低。本文采用的二维圆柱形亚波长结构只需要一次刻蚀即可，适合高精度批量生产。

亚波长结构相当于多层折射率渐变的薄膜，可以降低菲涅尔反射[2]，通过改变它的形状、周期、占空比、刻蚀高度等参数，得到不同的等效折射率，用于增加光学元件表面透过率。亚波长结构的制造工艺有很多[3，4]已经成功应用于太阳能电池表面等。由于亚波长结构形状的不同，可以将其应用于抗反射薄膜[5]、滤波片[6]、闪耀光栅[7]等。通过严格耦合波理论计算可知，当亚波长结构周期足够小时，透射光不存在高级次衍射[8]，这使得亚波长结构的应用得到拓展。由于全介质亚波长结构对光相位的调制能力，Philippe Lalanne等人提出高效率惠更斯表面[9]；由于全介质亚波长结构的会聚能力，Fanglu Lu和D.Fattal等人提出一维光栅透镜[10，11]。Paul R.West等人运用等效介质折射率理论，进行了圆柱形亚波长结构衍射透镜设计，制作了单个衍射透镜，实现了红外波段的高斯光束会聚[12]。但该结构口径有120μm，不利于集成化设计。

严格耦合波理论（Rigorouscoupled-wave analysis，RCWA）和等效介质折射率理论（Effective medium theory，EMT）已经证明了亚波长结构等效折射率随占空比增大而增大[13，14]。本文利用时域有限差分方法（Finite difference time domain，FDTD）计算等效折射率，并列出不同半径亚波长结构的等效介质，通过计算结果设计一个口径仅有4μm，厚度仅为1μm的衍射透镜，以实现在折射率为1.4的介质中对400nm～800nm波段的会聚。该方法可用于设计满足光学系统集成化要求的衍射透镜，有利于集成芯片批量生产。

1 理论基础

1.1 计算亚波长结构周期

光透过光栅后，会产生高级次衍射光，根据光栅常数与衍射级次的关系，能设计出各种衍射元件。一维亚波长光栅使偏振态与光栅方向平行的光透过率大，与光栅方向垂直的偏振光透过率低，导致出射光偏振态与入射光不一致，因此本文主要研究圆柱形二维光栅。在FDTD软件中创建了圆柱型二维光栅模型，其折射率为1.4，周期为1μm，半径为400nm，设置X-Z平面为结构截面图，光源为X方向偏振的线偏振平面波，位于结构上方Z=0.8μm处，垂直射入结构，对其进行仿真计算，结果如图1所示。

图1 二维光栅衍射效果

图1（a）所示，深色区域为光强较大区域，浅色为光强较弱的区域，证明了该结构使出射光能量分布发生改变，不再是平面波。图1（b）为相位分布图，深色区域与浅色区域交替表示相位值为-π～π，波前相位图弯曲的地方光强大。图1证明了该二维光栅使光场能量重新分布，不再是均匀分布，具有多级次衍射光。这将导致所设计的衍射透镜具有多焦点，不利于成像和探测。

为了使光透过光栅后只存在零级衍射，高级次衍射光变成倏逝波，则需要光栅尺寸足够小。当光栅特征尺寸和入射光波长相当时，光场计算不能再用标量衍射理论，其矢量特性不能忽视，因此采用严格耦合波方法和时域有限差分方法计算光场分布较为准确。严格耦合波理论在衍射结构的分析和设计中得到了广泛的应用，是一种相对直接的、非迭代的、确定性的分析方法，根据严格耦合波理论[7]得出：

当入射光波为正入射（θ≠0°）时，反射波只存在零级衍射，须满足：

透射波只存在零级衍射须满足：

其中，θ为入射角度，其中λ为入射光波波长，n1为空气折射率，n2为基底折射率。为了使任意角度入射光波透过圆柱形亚波长结构后不存在高阶衍射，取θ=90°，由公式（2）可知其周期应该满足：

取基底折射率为1.4时，针对入射光波段为400nm～800nm，其亚波长结构周期必须满足0＜Λ＜166nm。取周期为100nm时，即可满足消高级次衍射光的条件。如图1所示为周期100nm，半径为40nm的圆柱形亚波长结构。

图2 圆柱形亚波长结构

当光栅结构尺寸过大时，光透过光栅结构会产生高级次光，通过严格耦合波分析，得出消除高级次光需要满足的周期条件，并选择了结构周期为100nm的圆柱形二维亚波长结构，能满足消透射光高级次的要求。

1.2 计算亚波长结构等效折射率值

时域有限差分方法是Kane S.Yee提出的方法，将解域离散化成空间网格，并把带时间变量的麦克斯韦旋度方程转化为差分格式，并采用空间、时间差半个步长的离散网格形式，用前一个时刻的电场值和磁场值，得到现在时刻的电场值和磁场值，并在每一时刻都计算空间域的电磁场。每个磁场分量由四个电场分量环绕，每个电场分量由四个磁场分量环绕。取样方式符合法拉第电磁感应定律和安培环路定律。电场和磁场在时间上交替抽样，抽样时间彼此相差半个时间步。

为计算周期100nm，半径不同的亚波长结构的等效折射率值，采用软件FDTD-solutions对不同半径的亚波长结构进行仿真模拟，从相位延迟量计算出亚波长结构的等效折射率。建模结构为半径40nm，周期100nm的亚波长结构，将入射光设置为X轴向的线偏振平面光，为避免产生边缘效应使平面波波前变形：与光轴平行的方向采用周期性边界条件，与光轴垂直方向采用完美吸收匹配层。沿Z轴方向上，0～2μm处为亚波长结构区域，2～4μm处为空气。结果如图3所示，图3a、3b、3c、3d分别表示E矢量分布、H矢量分布和相位分布及沿光轴方向的相位曲线图。图3a、3b表示，有亚波长结构的区域，磁场和电场均被调制，但离开亚波长表面后，光波电磁场均匀，表明出射光依旧为平面波。图3c、3d表示，有亚波长结构的区域相比于无亚波长结构的区域产生相位延迟，根据相位延迟量可以计算该亚波长结构对应的等效折射率，计算原理为：

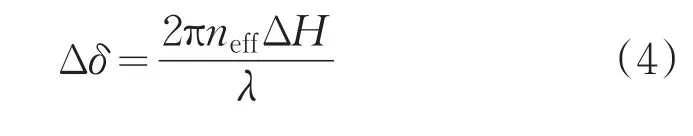
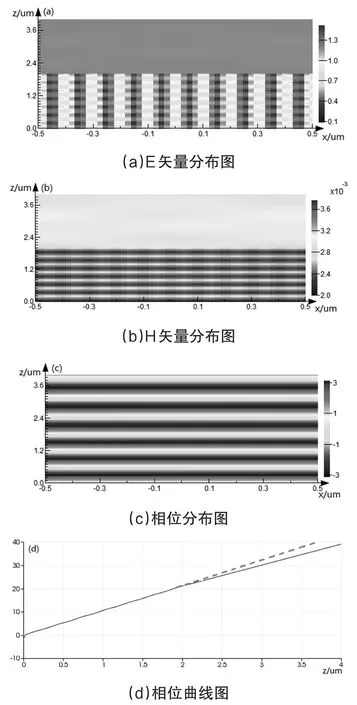
图3 圆柱形亚波长结构的波前调制能力

重复上述步骤，分别计算不同半径亚波长结构的相位随厚度H的变化规律，并利用公式（2）计算出等效折射率值，其对应关系如表1所示。

表1 半径与等效折射率值的关系

由表1可知，亚波长结构半径越大，其等效介质折射率越大，但半径与等效折射率值不成正比关系。

为了验证计算结果，并证明二维圆柱形亚波长结构确实能实现0～2π的连续相位调制，将建模改为：不同半径的亚波长结构依次从左往右排列开，得到一个调制波前的相位板，该相位板从左往右等效折射率依次增大。将入射光设置为沿X方向线偏振平面光，入射光波长为700nm，与光轴平行的方向采用周期性边界条件，与光轴垂直方向上采用完美吸收匹配层，探测器沿光轴方向放置，与光轴平行。

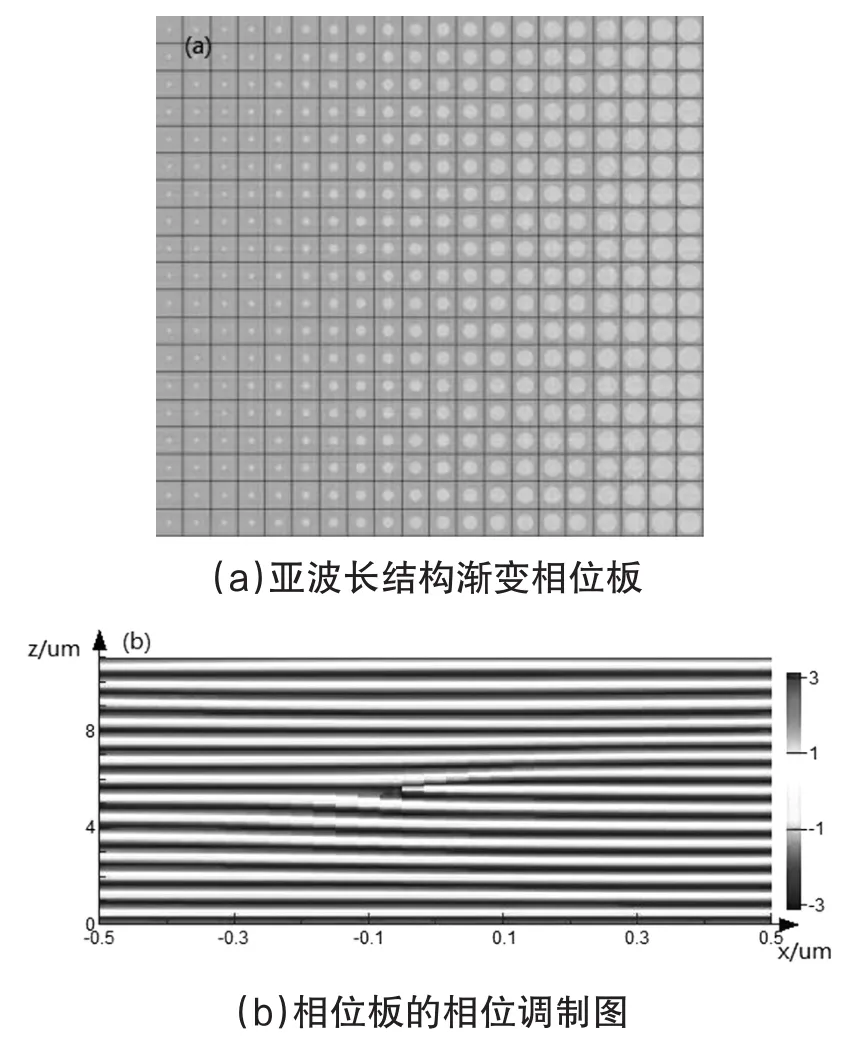
图4 亚波长结构连续调制相位能力

计算结果如图4所示。图4（a）为半径依次增大的亚波长结构，图4（b）为光通过相位板后的相位分布，深色与浅色线条表示相位由-π～π变化，左右两边正好相差一个2π。亚波长结构半径从左往右依次增大，相当于折射率从左往右逐渐增大的相位板，证明了二维圆柱形光栅确实可以实现连续相位调制。使得亚波长结构可以制作成涡旋光相位板，平面衍射透镜等。

2 设计与仿真

衍射会聚透镜需满足：透镜中心区域产生的相位延迟大于透镜边缘区域产生的相位延迟，由透镜中心向外相位延迟量逐渐降低。

2.1 全介质圆柱形亚波长结构透镜的设计

与衍射透镜和谐衍射透镜不同之处在于：其高度各处相等，只等效折射率值不同。因此，衍射会聚透镜需将半径大的亚波长结构排列在光轴附近，沿光轴中心向外径向依次减小，原理如图5所示，透镜中心等效折射率大，边缘等效折射率小。

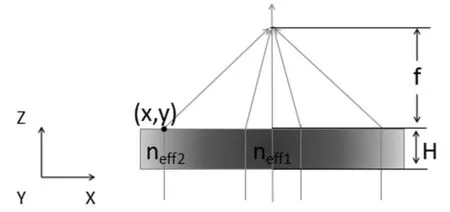
图5 衍射会聚透镜原理图

产生相位差与焦距的关系为：

其中，Δneff=neff1-neff2，(x,y)表示出射光位置坐标。

2.2 圆柱形亚波长结构透镜光强会聚仿真

对所设计的圆柱形亚波长结构会聚透镜进行仿真，采用400nm～800nm线偏振平面光入射到衍射透镜上，介质折射率为1.4，全介质圆柱形亚波长结构透镜厚度为1μm，口径为4μm。采用所有边界条件为完美吸收匹配层，得到光波会聚图样。图6（a）为各波长光垂直入射，透过圆柱形亚波长结构透镜后的坡应廷矢量分布。从左到右分别为800nm、640nm、533nm、457nm、400nm光入射，透过全介质圆柱形亚波长结构透镜后的会聚图样。深色区域表示光强最大，随着波长减小，焦距增大，由左向右图案表明，波长越小焦距越大。

图6 会聚光强图

图样表明亚波长结构可以在厚度为1μm的情况下，实现高数值孔径的会聚。同时能够观察到圆柱形亚波长结构透镜有与传统透镜相反的色差，800nm光焦距短，400nm光焦距较长。与传统透镜相结合时，可以有效消除色差。图6（a）为各波长光5°入射，800nm、640nm、533nm、457nm、400nm光透过亚波长结构透镜后的图样。

衍射会聚透镜用于集成光路中是很有意义的，能很大程度提高光学系统集成度，将该会聚透镜排列形成阵列，得到与光轴方向垂直的多光束会聚，相当于微透镜阵列，该系统的厚度仅为1μm，并且该衍射会聚透镜适用于所有光学材料，这增大了该衍射会聚透镜的适用范围。如图6所示为多光束会聚图样，入射光波长为800nm，与光轴平行方向为周期性边界条件，与光轴垂直方向为完美吸收匹配层。

图7 集成衍射型微透镜阵列会聚光强图

图7所示，阵列排布的衍射会聚透镜结构实现了数值孔径约为0.72的多光束会聚，该系统非常紧凑。微透镜阵列在均匀光系统、光场成像、波前传感器等领域有着广泛的应用。当光透过物体或物体反射时，波前相位发生变化，用集成微透镜阵列作为探测器，将探测器中小衍射透镜的会聚光斑位置读取出来，并反向计算波前信息，由波前信息又可以算出物体的面型特征。由于该芯片各个结构高度相同，因此只需要一次刻蚀即可，极大的提高了加工精度。

3 结论

本文提供了一种设计亚波长结构芯片的方法，通过时域有限差分方法计算出不同形状的亚波长结构的等效折射率值，并依据相位分布优化设计亚波长结构器件。亚波长结构不受基底材料的限制，光学材料都可以用于制作亚波长器件，因此，无论是单独使用亚波长结构制作的会聚透镜（阵列集成芯片），或是与传统光学系统相结合都是很有意义的。同时该结构只需进行一次刻蚀加工，使得加工精度得到很大提高。