浅谈“构造法”在解题中的妙用

（湖北省嘉鱼县教研室 湖北嘉鱼 437200）

构造法是运用数学的基本思想经过认真的观察，深入的思考、分析，迁移联想，正确思维，巧妙地、合理地构造出某些元素、某种模式，使问题转化为新元素的问题，或转化为新元素之间的一种新的组织形式，从而使问题得以解决，这种方法称之为“构造法” .

怎样构造呢？构造法的内涵十分丰富，没有完全固定的模式可以套用，它是以广泛抽象的普遍性与现实问题的特殊性为基础，针对具体问题的特点而采取的相应的解决方法，基本的方法是：借用一类问题的性质，来研究另一类问题的思维方法，在解题过程中，若按习惯定式思维去探求解题途径比较困难时，我们可以根据题目特点，展开丰富的联想拓宽自己的思维，运用构造法解题也是培养我们创新意识和创新思维的手段之一，同时对提高我们的解题能力也有所帮助。[1]

案例：人教版八（上）教材第130页第11题：一次越野赛跑中，当小明跑了1600米时，小刚跑了1450米，此后两人分别以a米/秒和b米/秒匀速跑，又过100秒时小刚追上小明，200秒时小刚到达终点，这次越野赛跑的全程为多少？[2]

思考：本题从表面上似乎与函数没有关联，但却可以构造函数关系并运用函数的相关知识予以解决，由于小明和小刚两人是匀速跑，我们可以将路程y看成是时间x的一次函数，依题意可画出如下函数图象（图1）：

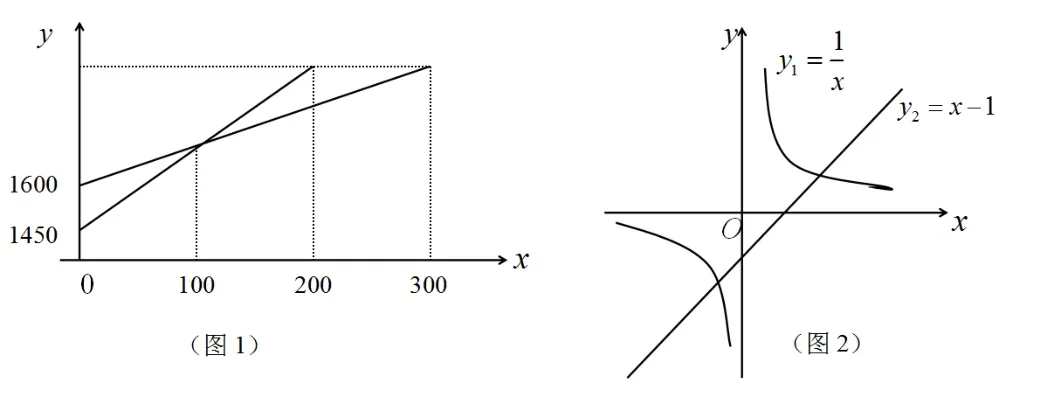
根据函数图象，可设y1=bx+1450，y2=ax+1600，当x=100时，y1=y2；当x=200时对应的与x=300时对应的相等，及100a+ 1600=100b+1450，200b+ 1450=300a+1600，联立解得a=1.5，b=3，故此次越野跑的全程为：200×3＋1450=2050.

回顾本题的解答过程，通过巧妙地构造一次函数并通过函数图象形象、直观地使问题得以解决，思维活跃，解法新颖，令人回味！

思考：尽管本道题超出了课程标准要求（可化为一元二次方程的分式方程问题），但我们仍能打破常规，从中体会到构造法的妙用！可以将方程两边分别

反思：本道题的初衷是将分式方程转化为一元二次方程，再通过判断一元二次方程解的个数得到原分式方程解的个数，可在上述解决问题过程中，通过构造两个函数，将判断方程解的个数问题转化为判断两个函数图象交点个数问题，既体现了方程与函数的本质联系，又发散了思维，培养了创新意识，数学课程标准（2011版）明确指出，创新意识的培养应该从义务教育阶段做起，贯穿数学教育的始终，而创新意识正是学生所缺乏的.我们不能错失这样的好机会！

可以看到，构造法虽然算不上是解决数学问题的一般方法，其技巧性较强，但是在数学很多领域都有它的身影，只要我们发散思维，丰富联想，合理构造，勇于创新，它就在你身边！对“构造法”的理解和运用有助于我们打破思维定势，完善思维品质，达到解题境界上的升华！