一道方程题的证明过程

（浙江求是工程咨询监理有限公司 江西鄱阳 333126）

已知方程：axm-byn=R，其中，其中a，b，R为给定的正整数，且gcd（a，b）＝ 1，x，y，m，n都属于正整数。

求：方程axm-byn=R仅有有限组解（x，y，m，n）。

解：设axm=AC2；byn=BC2，R=AB2

则方程axm-byn=R

可转化成AC2=BC2AB2

于是根据三角形的勾股定理性质可得（如图1）：

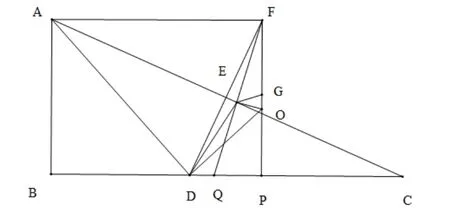
图1

则，在BC边上取一点D，使BD＝AB

连接AD，作AF⊥AB交AB于 点A，其中AD＝AF，过AF⊥BC交BC于点P。

由AF⊥AB，FP⊥BC，AB⊥BC

⇒四边形ABPF为矩形

另在AC边上取点E，使AE＝AD

又∵AD＝AF

⇒AE＝AD＝AF

⇒点D，E，F三点共圆

过AD⊥DO交FP于点O

∵PF⊥AF，且D，E，F三点共圆

⇒OF＝OD

连结EO，作EG＝EO交FO线段于点G

⇒∠EGO＝∠EOG

本题分为以下几个步骤解析

（一）

（二）

即，当∠ODE＝∠DEO＝22.5°时，在Rt△ABC中，AC和BC仅有有限组解（k＜AC＜2.29k，0＜BC＜2.06k）

（三）

当∠EDO＝22°时，∠DEO＋∠DOE＋∠EDO＝180°

⇒∠DEO＋∠DOE＝158°

分析1）：在△DEO中，当∠DOE＜∠DEO时

根据三角形的余弦定理可得

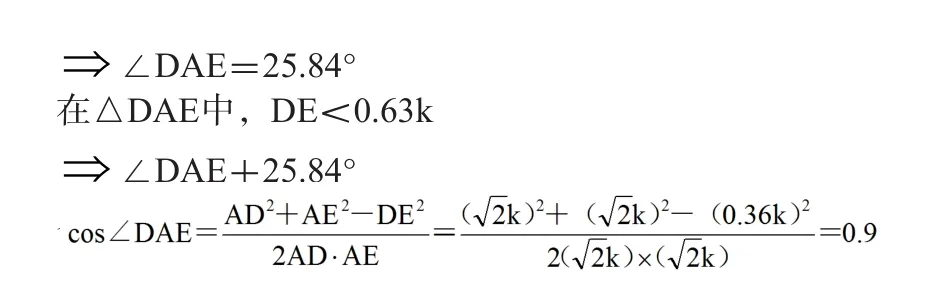
即，当∠DOE＜∠DEO时（∠DOE＜79°），在Rt△ABC中，AC和BC仅有有限组解。

2．当∠DOE＞∠DEO时，∠EDO＝22°

取EF＝0.24k，根据三角形余弦定理得

即，当∠DOE＜∠DEO时，在Rt△ABC中，AC和BC仅有有限组解（k＜AC＜2.93k，0＜BC＜2.75k）。

（四）

当∠EDO＜22°时，由∠QFP＝∠FDE，且∠EDO＋∠FDE＝22.5°

即，当∠EDO＜22°，在Rt△ABC中，AB和BC仅有有限组解。

综合上述（一）（二）（三）（四）可知，在Rt△ABC中，已知AB＝k，则AC和BC的解仅有有限组解（AC，BC）

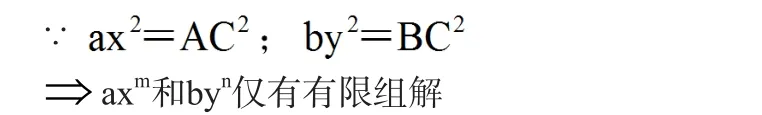
又∵a和b为给定的正整数，且gcd（a，b）＝1

⇒方程：axm-byn=R在a，b，R为给定的正整数时仅有有限组解（x，y，m，n）。