浅谈初中代数式最值的求解技巧

（福建省泉州市第七中学金山校区 福建泉州 362000）

在生活实践中，人们经常面对带有“最”字的问题，如花费最低，面积最小，产值最高，获利最大等。近年来各地中考题中最值问题更是频频出现，问题背景新颖，常出现的最值问题有应用题、几何动态、函数最值等。在初中数学竞赛中整式、分式、二次根式、函数、多元方程等形式也常求某个变量或特殊结构代数式的值。最值问题构题精妙，牵涉的知识点多，解题方法灵活多变。下面就本人在初中阶段的教学谈谈较常见的最值问题的求解方法，以便大家举一反三。

一、直接代入计算，穷举获取法。

例1：已知点A（1，a），B（-2，b），C（0，c）都在函数y=1-x的图像上，求a,b,c的最大值。

分析：将三个点代入函数解析式，易知a= 0,b= 3 ,c=1，所以a,b,c的最大值是3

二、建立函数模型求最值：利用函数图像的增减性。

初中阶段的重点函数是一次函数与二次函数，利用函数的单调性来解决应用性问题的最值，要注意先引入变量，列出函数关系式，尤其要注意求出自变量的取值范围及区间范围对最值的影响。在例1中可知一次函数y=1-x中，所以由一次函数图像的性质知y随着x的增大而减小，又因为-2＜ 0 ＜1，所以b＞c＞a，所以a,b,c的最大值是b，再求出b=3。2018年福建中考数学第23题重点考查了二次函数的区间最值。

解析：第（1）步易由一元二次方程求解

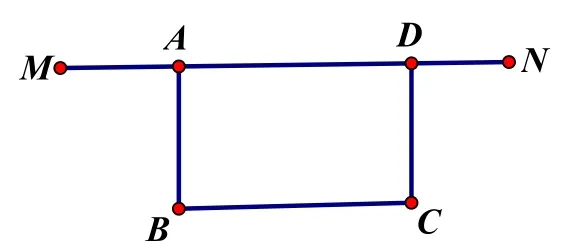
第（2）步，设AD＝x米，矩形菜园ABCD的面积为S平方米，

学生易忽略A D≤a这个条件的限制，很多考生忘了分类讨论。①当a≥50时，由于抛物线开口向下，顶点为（50，1250）且x≤a，所以当x= 50时，S 最大值是1250平方米；②当0＜a＜ 50时，则0＜x≤a在对称轴x=50的右侧，此时S随着x的增大而增大，所以当x=a时，

S最大＝

本题不仅考参查了二次函数的最值，而且考查了学生的分类讨论能力、对参数范围的理解，值得老师与学生高度重视。

三、用根的判别式法，在方程有解的条件下求最值

例3：在2017年福建中考数学第25题压轴题中问题的核心是：已知直线y=2x+m与抛物线y=ax2+ax+b有一个公共点M（1，0）及另一个交点N，且a＜b.求△QMN面积的最小值。又求得点M（1，0），点

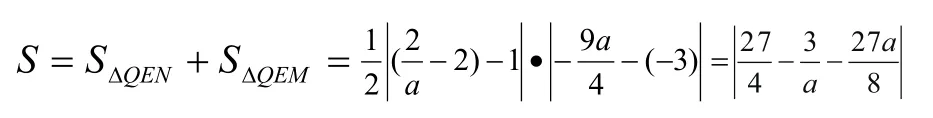
初中学生对含有分式形式的代数式的最值是很陌生的，如何引导他们在能力范围内解决这个问题呢？可以借助“主元思想”、“去分母”技巧，化分式为整式方程，整理得（★），把它看成以a为主元的一元二次方程，a有实数解，所以

四、利用配方法及基本不等式、因式分解等代数式的恒等变形技巧解决最值。

1.利用基本不等式、配方思想求最值。

例4：设a,b,c为正数，且abc(a+b+c)=4，则(a+b) (b+c)的最小值。

解析：

由此可以想到：

解：法一：将y看成参数，按x作降幂排列，再配方。

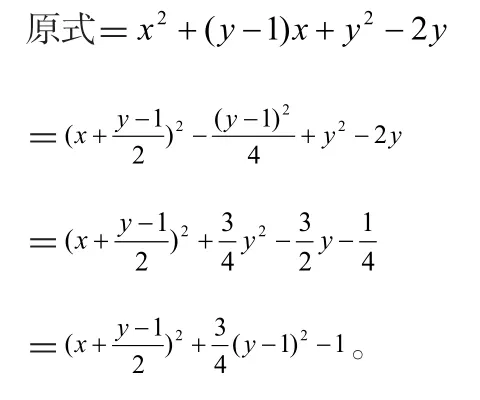
当且仅当y= 1 ,x=0，原式取到最小值-1

用配方法求代数式的取最小值，要注意两个完全平方式能否同时为0，即最小值能否取到。

法二：（本题也可以用根的判别式法）

设t=x2+x y+y2-x-2y，整理成关于x的一元二次方程x2+(y-1)x+y2-2y-t=0，

则Δ=(y-1)2-4(y2-2y-t)=-3y2+6y+1+4t≥0，

2.利用解多元方程组、不等式的性质求最值

解析：由x1,x2,x3, … ,xn都是整数，且-1≤xi≤2(i= 1 ,2,3…,n)可设这n个整数中有a个-1，b个1，c个2，

得2b+6c=118，即b+ 3c=5 9，

解得b=5 9 - 3c,a=-c+4 0（0≤c≤ 1 9）

所以1 9≤w≤133

当c= 0,b= 5 9,a=4 0时，w的最小值是19；当c= 1 9,b= 2,a=2 1时，w的最小值是133

3.用换元法、待定系数法、韦达定理、因式分解等技巧求竞赛中的最值问题。

例7：设x,y都是正整数，且有的最大值。

解析：依题意知x-116,x+100,y都是整数，所为x- 1 16 ,x+100必为整数，设x-116 =m2,x+100=n2(m＜n，且m,n都是正整数），因式分解得(n+m) (n-m)=216=4×5 4=2×108，所以当m+n=108时，y有最大值，且最大值是108

例8：若实数x,y,z满足，求z的最大值。

解析：

由x+y= 5 -z,

x y=3-(y z+z x)=3-z(x+y)=3-z(5-z)=z2- 5z+3，所以运用韦达定理构造二次方程a2-(5-z)a+(z2-5z+3)＝0，因为a有解，所以Δ=(5-z)2-4(z2-5z+3)=3z2-1 0z-1 3≤0，

五、用放缩法求代数式的最值

这种方法在在高中数学中用得较多，这里就不再举例说明。

从以上分析论述可知：最值问题的解决并不是绝对孤立不变，有时可以一题多解；有时需要多种方法一起使用才能灵活解决问题。解题时，要仔细观测代数式的结构特点，以便选择合理的解题方法，做到快速解题。同时要说明最值在什么情况下可以达到，以养成严谨思维的习惯。