小学生几何概念形成的途径及教学思考
2018-12-17
(重庆市沙坪坝小学 重庆 400030)
《义务教育数学课程标准(2011年版)》基于数学这样定义到:数学是研究数量关系和空间形式的科学。显而言之,空间形式的研究对于小学生而言,意义是非凡的。然而在小学阶段的几何教学中,涉及到的几何概念繁多,且由于几何概念固有的高度抽象性和普遍性适用性的特点,使得部分孩子在掌握几何概念的过程中存在着一定的困难。[1]
心理学对“概念”这样界定:概念属于理性思维的基本形式之一,是客观实物的本质属性在人们头脑中的概括反映。人们在感性认知的基础上,从同类事物的许多属性中,概括出其所特有的属性,形成用词或词组表达的概念。概念具有抽象性和普遍性,因而能反映同类事物的本质。[2]
结合自身的教学实践,特此对小学生几何概念教学进行了初步的分析与思考,并作出如下的梳理。
一、概念抽象的两个措施
“概念是客观实物的本质属性在人们头脑中的概括反映,人们在感性认知的基础上,从同类事物的许多属性中,概括出其所特有的属性。”因此,几何概念的形成必须是要在众多的图形属性中,去找到该图形的本质属性。在这样的经历过程中,合理运用比较和分类,有利于帮助学生概括概念的本质属性。
1.比较。
在小学生的意识中,有很多概念性的认识在他们的头脑中已经有了足够的判断经验,但是如果要让他们用规范、简洁的语言来表达的话,就比较吃力了。所以,在教学几何概念的时候,老师可以利用这样的儿童认知心理水平,有意识的设计一些非本质的特征,让孩子在认知矛盾冲突中自己判断,然后一步一步的“逼近”概念的本质,让其抽象出概念的内涵,并能用自己的语言恰当的表达出来。
2.分类。
“分类”即是指按照种类、等级或性质分别归类。(语出《书·舜典》附亡《书》序:“帝釐下土,方设居方,别生分类,作《汩作》。)
比如:当我们学习了普通三角形的概念后,要进一步学习直角三角形、锐角三角形、钝角三角形的时候,我们就可以给学生提供若干三角形,让学生对这些三角形进行分类。
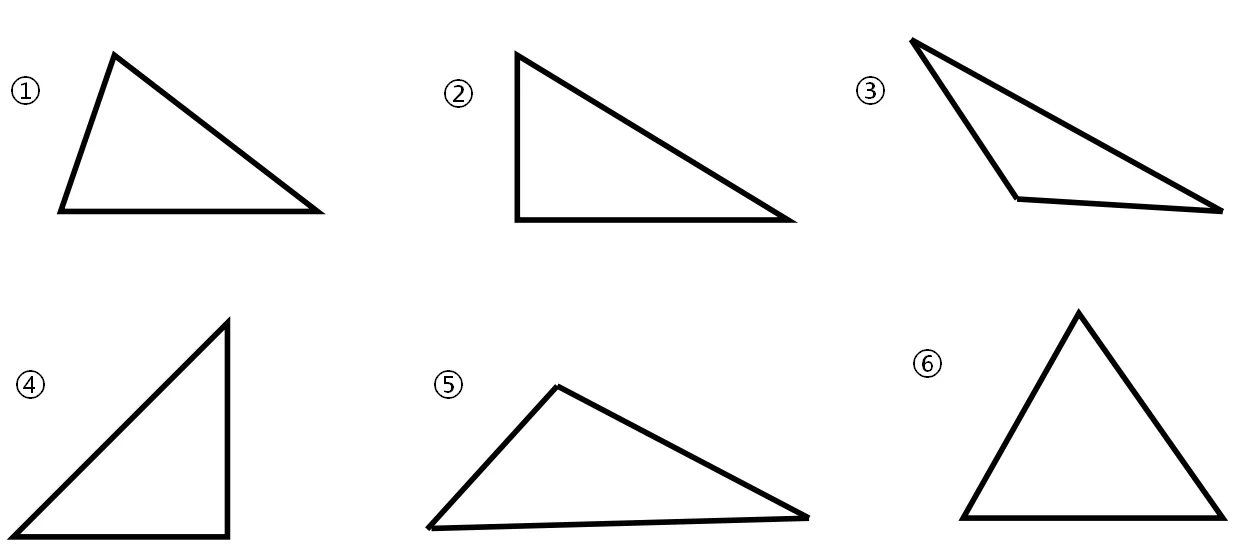
学生通过思考操作,会将①和⑥、②和④、③和⑤分别归为一类。这时就可以让学生说一说自己的想法,由此让学生梳理出相同类别三角形的共同属性,即“第一类三角形三个角都是锐角,第二类三角形有一个角是直角,第三类三角形有一个角是钝角。”这样,学生在通过分类的活动中,就分别找到了锐角三角形、直角三角形和钝角三角形概念的本质属性,由此得出这三种三角形的概念。这样的操作,可以让孩子对概念的理解更深刻,对概念本质的掌握更牢固。
二、概念教学的三个层次
1.借助实践操作,概括几何概念的特征。
任何一个几何图形的特征的获得,都是学生思维活动的结果。那么,儿童思维是从哪儿来的?瑞士心理学家皮亚杰提出这样的观点:儿童的思维不是单纯的来自客观物体,也不是单纯的来自主体,而是来自主体对客体的动作,是主体与客体相互作用的结果。
所以,当我们要让我们的孩子对一个几何概念进行认识的时候,我们必须要给孩子提供具体的、现实的实物学具。鼓励孩子通过自己的多种感官(包括视觉、触觉等)进行体会,并结合具体的感知进行体验,形成属于自己的知觉雏形。
比如:当我们教学三角形的时候,教师往往会给孩子提供一些三角形的学具,让孩子先看一看、摸一摸、想一想,然后再来说一说“三角形有什么特征?”
学生的回答也许是这样的:(1)三角形有三条边(2)三角形有三个角(3)三角形有三个很“尖”的地方,还很扎手(4)三角形的面是平的(5)三角形的边是直的……
在这个过程中,学生就动用了自己的视觉和触觉,并能够将自己感知到的“特征”进行思维加工,得出自己的“三角形概念”。或许此时的概念并不准确,有的不够简化,有的不够健全,但是,这都不妨碍孩子思维的发展。
2.认真分析归纳,抽象几何概念的内涵。
一个几何图形的特征往往是多方面的,但是其本质特征则是需要在这些众多的特征中去进行分析、归纳,最终抽象出属于这个“概念”的本质内涵。同样借用上述例子分析:当孩子通过多重感官获得了众多的三角形的特征后,这时老师可再提出一个核心问题:你认为什么样的图形是三角形?这时学生就会根据上述的特征,自己想办法去组织语言来描述“什么图形是三角形?”
学生的概括可能不会很精简,这时教师可以适当的提出疑问。比如:当有学生概括出“有三条边,三个角组成的图形就是三角形。”很明显,学生的头脑中这个图形一定不是三角形,那么问题出现在哪里呢?鼓励学生自己发现。哦!每条边必须是“直”的。教师又可以追问:我们学过 的“线”中,哪些是直的?你认为这里应该用什么“线”来描述合适。通过这样的实践操作,孩子进一步的得出三角形概念的内涵包括“三条线段”,那么这三条线段是怎样摆的呢?再进而得出“围成”,有了三条线段“围成”的描述后,“有三个角”也就可以不必再叙述了。
如此的分析与归纳,让孩子从众多的特征中逐步抽象出概念的本质内涵,这其实就是对孩子空间思维能力的有效培养。
发展孩子的几何直观和空间思维,帮助孩子有效形成几何概念,形象是前提,表象是基础,抽象是本质。综上所述,即是我在教学实践中的一些初步感悟和体会。
