深度挖掘教材,展现思维过程
2018-12-15王圆月
王圆月

【摘 要】 教材是人类知识及其精神产品的精华,是学校教育资源目标的重要载体,也是教学的重要资源。教师做为学生学习、成长的引导者,对教材的领悟程度直接关系到教材目标的实现程度,教师在备课时,需要解读教材、正确理解和把握教材的价值取向和分析学生的特点,结合教材的重点和难点,设计有针对性的教学环节。
【关键词】 数学教材;深度挖掘;思维变式
数学课本除了仅有的一点文字,尽是大量的数字和字母,难得出现一幅画,却只是简单的线条。以前我认为课本价值不大,原因是书上的问题太简单了,恐怕不能提高学生的能力,因此备课时把大量的时间放在了一本本教辅资料上。由于教师的浅显认识,在学生眼中数学课本似乎可有可无。其实数学课本不同于一般参考材料或其他一些读物,它是按照学科系统性结合学生认知规律,以简练的语言呈现数学知识的。知识结构虽然存在,但思维过程被压缩。学生看到的往往都是思维的结果,看不到思维活动的过程,思想、方法更是难以体现。课本呈现的是一幅幅知识的框架,要让课本生动起来,就需要教师对课本内容添砖加瓦,体现数学本身那种令人倾倒的丰满的内容,体现思维过程和思想方法。这样不仅使学生掌握书本上看得见的思维结果,更让他们参与那些课本上看不见的思维活动过程。
华东师大版2013新教材八年级上73页-75页13.2.6节《斜边直角边》知识简单,内容很少,一个做一做、一句全等方法总结、一个例题。10分钟讲完知识,再从其他教辅资料上找些练习题让学生强化,但这样的课堂显得单调、死气。于是我通过对本节内容的补充和延伸后,学生学到的不只是一种全等的判定方法。
一、延伸“做一做”,诱发思考,渗透分类讨论思想
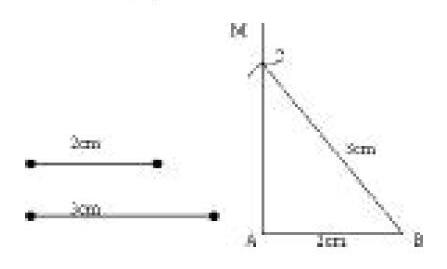
课本上P74“做一做”要求分别以2cm、3cm为直角边和斜边画一个直角三角形。等同学们按课本步骤画好后,我提出问题:“我们画好线段AB后,还可以怎样画呢?”
学生甲说:“点C可以画在下方呀。”
学生乙说:“直角也可以在点B画,而且点C可以画在AB上面也可以在AB下面。”
学生画出了以下四种情形
学生丙说:“还可以先把斜边画出来……”
师:“很好!然后呢?同学们试一试能否画出来?”先让大家画出一条3cm的线段。接下来,同学们发现,线段的两端只能画锐角不能画直角,可是锐角的度数无法确定。
师:“这四种情形的三角形什么关系呢?”
学生:“都是全等的。”
师:“说明斜边和一条直角边分别对应相等的两个的直角三角形全等。”
课本上虽然只给出了一种情形,但它本身包含了多种情形,需要师生一起去发现,这其实也是教材的编者们有意留给教师发挥的空间。对于一些爱思考的学生,他们会产生疑问,若不按课本上的步骤画,会出现什么情形?若教师一言带过,反而忽视了他们的对数学的热爱。而对于不太主动的学生来说,若教师不引导,他们便不会再去思考,这样反而会更让学生的思维更懒惰。对做一做的延伸,不只是分类讨论这一重要思想的渗透;同时还教会学生要善于发现问题,敢于创新。
二、解读“斜边和一条直角边分别相等的两个直角三角形全等”,全面、深入理解全等的判定
师:“用H.L.判定全等的前提是什么?”
生:“两个三角形都是直角三角形。”
师:“在已知了哪些等量关系后,可以用H.L.?”
生:“斜边和一条直角邊相等。”
师:“请看这幅图,已知了两三角形是直角三角形,要用H.L.判定图中两三角形全等,还需什么条件?”
学生甲:“AC=DF,AB=ED”
学生乙:“AC=DF,BC=EF无论怎样,用H.L.必须有斜边相等。噢,还可以吧BC=EF换成BF=EC。”
学生丙:“看似只需要两个条件,实际上得找到三个条件。”
教师板书后。
师:“直角三角形也是三角形,以前的四种方法也可以用。现在请同学们自己补充条件,来得到两个三角形全等。例如要用A.S.A.还需添哪些条件?”
生:“∠A=∠D,AB=DE,或者∠ACB=∠EFD,BC=EF。”
师:“还可以怎样改呢?角相等可以通过什么得到?”
生:“AC∥FD,那有好多种做法。”
师:“是的,只要你们愿意动脑,方法比总是问题多。现在请同学们自己提问,叫其他同学回答。”
大家都争先恐后地举手提问……
学生丁:“老师,我可以把问题出难一点吗?”
师:“可以。”
学生丁:“我添AC=FD,BF=CE,求证AC∥DF,我想让刘忻回答。”
刘忻:“由BF=CE可以得出BC=EF,又因为AC=FD,它们是直角三角形,可以用H.L.得到全等,则∠ACB=∠EFD,所以AC∥DF。”
新知识结合已学的知识,形成知识体系,让学生全面掌握。并且通过教师引导,让学生自己提出问题,能让学生更深地理解所学知识。同时学生积极参与,体现了学生的主体,是对学生的更高要求,课堂也不再死气沉沉。
三、例题变形记,小例题,大收获
上一环节完成后,让学生自己解答课本上例题,再与课本上的解答对照。然后我通过对例题的变式,让这个简单的例题丰富了起来。
变式一:变结论
因为由原例题学生已经得出△ABC≌△BAD,所以起初我以为学生会通过∠CAB=∠DBA,直接得出AO=BO。可是大部分学生是由△ABC≌△BAD得出AD=BC,然后通过A.A.S.得出△ADO≌△BCO,最后得出AO=BO。学生尽管做对了此题,但是并没有了解透彻,原因是对于找等量关系,学生很容易找到明显的量,而对于有重叠部分的角或线段学生往往忽略,这也是为什么一旦问题复杂了许多学生便无处着手的原因之一。因此通过此题让学生体会到,每一个已知条件或证得的结论,都必须好好利用,在图中仔细找隐含的关系。
变式二:变已知
我要求学生用不同的方法解答。法一:可以直接用A.A.S.得出△ABC≌△BAD,则BC=AD。法二:先得出AO=BO,然后用A.A.S得出△ADO≌△BCO,则BC=AD。
变式三:变图形
此时学生能马上想到简便做法“连接AB”,用H.L.证△ABC≌△BAD,则AC=BD。也有学生想到用A.A.S.得出△ADO≌△BCO,就有DO=CO,AO=BO,则AC=BD。由于此题是在例题的基础之上变形得到的,学生能马上找到简便方法,因此在一段时间之后或复习时还可以让学生用不同方法练习此题。
以上三个变式都可以用两种方法作答,既打开了学生思维,也让学生从中体会到数学的乐趣。
原本10分钟就可以讲完的内容,花了快一节课的时间。在这节课上,学生是快乐的,学生动手、动脑、动口,全面参与,学到的不只是H.L.,还有如何思考问题,如何在问题中找到解决办法。
而这一切都来源于课本,来源于课本上字里行间隐藏的思维过程。
【参考文献】
[1] 刘润珍. 挖掘教材习题,提高数学素养[J]. 青少年日记(教育教学研究),2018(1).
[2] 邱利娟. 挖掘教材内涵巧设数学游戏课[J]. 新课程(小学版),2018(3).
