高压断路器瓷套裂纹的数值建模及临界尺寸研究

，

(1.国网盱眙县供电公司，江苏 盱眙 211700； 2.国网淮安供电公司，江苏 淮安223001)

0 引言

大量断裂事故分析表明，因结构中存在裂纹而引起的断裂失效是工程中最常见、最重要的失效模式[1]。高压断路器瓷套断裂会严重危害电力系统的安全稳定运行，而瓷套往往存在因陶瓷材料本身缺陷或制造、使用所产生的裂纹，为确定瓷套能否继续安全使用，最重要的就是判断裂纹是否会失效扩展，从而导致瓷套断裂。断裂力学指出[2]：裂纹的尺寸若小于材料断裂的临界尺寸，则可继续安全，反之则会发生断裂。因此，为保证高压断路器瓷套的安全运行，需计算出导致瓷套断裂的临界裂纹尺寸。

文献[3]根据支柱瓷绝缘子的简化力学模型和断裂力学相关理论，分析了瓷绝缘子的临界裂纹尺寸及其无损探伤的灵敏度。文献[4]通过有限元法计算了瓷绝缘子的结构应力，并根据断裂力学的相关理论计算了其临界裂纹尺寸。文献[5]通过断裂力学的方法分析了碳化硅陶瓷的临界裂纹尺寸大小。文献[6]建立了瓷套的有限元模型，分析了瓷套的应力分布情况，基于断裂力学的方法获得了瓷套的临界裂纹尺寸大小。以上文献在计算陶瓷材料断裂的临界裂纹尺寸时，都是根据断裂力学理论推导临界裂纹尺寸简化的解析表达式，对于瓷套等复杂几何构件误差较大，临界尺寸的精确性难以满足要求，也并未对瓷套裂纹的临界尺寸分布规律进行深入研究。

笔者建立了高压断路器瓷套及其裂纹临界尺寸的数值计算模型，计算研究了不同位置、不同长深比和不同弯曲载荷下的临界裂纹尺寸及变化规律，为瓷套的无损探伤及运行状况评估提供有效的理论参考和技术支持。

1 应力强度因子的数值计算方法

在断裂力学中，应力强度因子是含裂纹结构断裂的重要判断参数，其求解方法主要有解析法、权函数法、有限元法等[7]。有限元法因具有强大的建模能力，适用于复杂几何模型和各种边界条件，并能保持较高的精度，效率高、成本低，已成为求解应力强度因子最广泛、最有效的方法。裂纹应力强度因子的有限元法求解法包括位移法和积分法等，相互积分法从能量角度出发，计算的结果具有更高的准确度，且相互积分法只需进行一次后处理，求解更加简便[8]，因此，本文在有限元法求解应力强度因子时采用相互积分法。

相互积分法最先由Stern为分离二维裂纹应力强度因子而提出，GOSZ等将其进一步推广到三维裂纹应力强度因子的求解[9]。根据断裂力学相关理论可知

(1)

(2)

式中：T为在积分边界上所作用的力；u、s分别为边界上的位移大小和弧长；W为材料的应变能密度；εij为部分应变值。

将模型所受真实载荷形成的裂纹尖端场与一个可设计的辅助裂纹尖端场进行叠加，结合式(1)和式(2)可得：

式中，M(1,2)为真实场与辅助场的相互作用积分，其表达式为

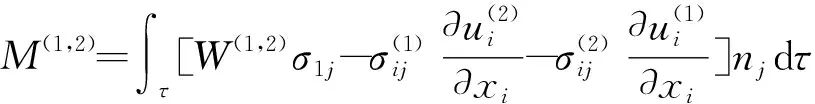
(4)

应力强度因子和相互作用积分的关系为

(5)

对于平面应变满足E*=E/(1-ν2)。

2 高压断路器瓷套裂纹的数值建模

2.1 高压断路器瓷套基本结构

以500 kV电压等级户外式断路器为例，断路器灭弧介质为SF6，其瓷套的组成主要包括铸铜法兰、水泥胶合剂、瓷套本体以及自由侧的接线端子板和外接导线等部分，其结构简化示意图见图1，主要几何尺寸参数见表1。瓷套本体主要作用为承载和绝缘，采用的材料为氧化铝陶瓷，水泥胶合剂为铸铜法兰和瓷套本体间空隙处的填充剂，断路器通过接线端子板与外导线相接[10]。高压断路器瓷套在其服役过程中的主要受力有瓷套自身及其金属附件的重力、瓷套腔内SF6气体向外作用压力、温度热应力、外接导线拉力以及短路电动力、风力等动态作用力，高压断路器瓷套组成部分所采用材料的性能参数见表2。

图1 高压断路器瓷套简化结构图Fig.1 Simplified structure of high voltage circuit breaker porcelain bushing

表1 断路器瓷套主要几何尺寸参数Table 1 The main geometry size parameters of circuit breaker porcelain bushing

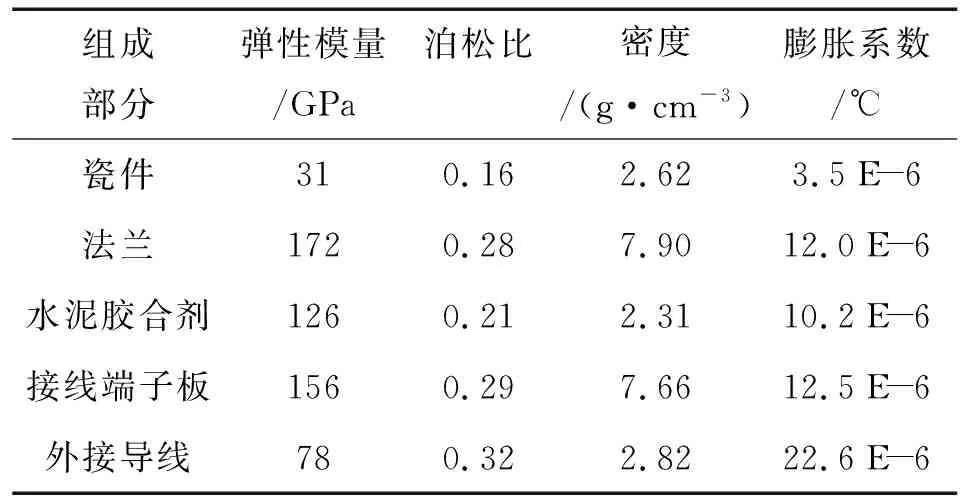
表2 瓷套组成部分材料性能参数Table 2 Material performance parameters of porcelain bushing component

2.2 断路器瓷套的热-结构耦合数学模型

高压断路器瓷套在其服役过程中受到的主要应力为温度热应力，即因瓷套法兰、水泥胶合剂和瓷套陶瓷本体材料线膨胀系数不一致而产生的热膨胀力，热应力大小与瓷套所处环境温度相关，在冬季低温条件下该力最为明显[11]，因此，断路器瓷套的温度场与结构场之间存在着相互影响和作用，瓷套受力是热-结构耦合作用的结果。

对于体积为V、边界为S、质量密度为ρ的连续介质，其能量平衡方程和力平衡方程可表示为[12]

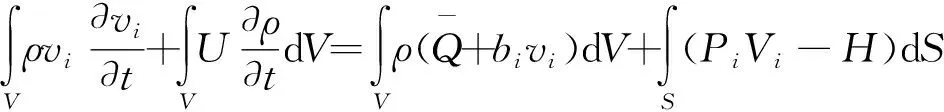
(7)

用柯西应力来表示压力，则根据式(6)和式(7)可得热-结构耦合分析的能量方程为

(8)

由虚功原理可知结构位移ui需满足关系：

(9)

不考虑惯性作用，并假设物体的能量方程和力平衡方程均建立在当前的构型上，则可用弱耦合的增量非线性有限元法对热一结构耦合进行处理，得到的结构温度场和热应力应变场的有限元方程可表示为

(10)

式中：KU、MT分别表示力学刚度和热学刚度矩阵，MU、CU分别表示热力耦合矩阵和热容矩阵，u(t)、T(t)分别表示点位移矢量和节点温度矢量。

2.3 裂纹临界尺寸的数值计算方法

三维裂纹体的有限元建模主要有两种方法：逐节点直接建模法和实体建模法[13]。逐节点建模法为节点—单元—结构逐步建模，该方法工作量大，建模繁琐，不适用于复杂几何结构，而实体建模法采用“自上向下”的整体建模思路，复杂结构适应性很强，而且具有很好的精确度。工程实践表明，Ⅰ型(张开型)裂纹是瓷套发生断裂的主要原因，同时也是最危险的裂纹形式，而且当实际裂纹为复合型裂纹时，也可将其等效为Ⅰ型裂纹处理[14]，因此本文研究主要针对Ⅰ型裂纹形式。结合裂纹实体建模法和应力强度因子的相互积分法求解方法，可得瓷套裂纹临界尺寸的数值计算方法，具体步骤：

1)根据瓷套的结构参数和力学参数，建立不含裂纹缺陷的瓷套模型，并设定断裂的允许应力强度因子差ΔK。

2)根据裂纹的类型，设定初始裂纹临界尺寸并建立相应类型及尺寸的裂纹辅助模型。

3)根据所要求的裂纹位置的临界尺寸，将建好的裂纹辅助模型移至无缺陷模型的相应区域，并进行相应的布尔操作，获得含裂纹缺陷的瓷套模型。

4)对裂纹辅助模型的面采用MESH200单元进行网格划分，并在裂纹尖端通过设置奇异点来生成二维奇异单元，然后将所生成的面网格沿裂纹深度方向通过体扫掠方式生成三维单元，并对面网格做清除处理，裂纹前缘采用的是solid186单元退化生成的三维退化奇异等参单元。非裂纹区域采用自由网格划分，模型中裂纹与非裂纹的过渡区域可采用多点约束法(MPC)进行连接。

5)对模型施加相应的边界约束条件，根据瓷套实际所受载荷施加相应的载荷，采用相互积分法计算裂纹尖端应力强度因子。

6)对计算得到的应力强度因子K与瓷套陶瓷材料本身断裂韧性所对应的临界应力强度因子K0进行比较，若|K-K0|<ΔK，则当前裂纹尺寸即为所要求的临界裂纹尺寸，反之则对裂纹的尺寸进行相应的调整，重新进入步骤2)进行求解，直至获得满足|K-K0|<ΔK的裂纹临界尺寸。

基于有限元法的裂纹临界尺寸计算适用性强，且准确率也比传统的解析法要更高，尤其是在复杂几何模型及应力分布复杂的情况。裂纹临界尺寸的数值求解法在工程实践中获得越来越广泛的应用。

2.4 断路器瓷套的数值建模

有限元法是一种以变分原理和加权余量法为基础的偏微分方程数值求解方法，它最早应用于结构力学领域，随着计算机技术的快速发展，为有限元方法的发展提供良好的条件，有限元法在流体力学、电磁场等众多工程领域都得到了广泛的应用，并在实践中被证明是一种有效实用的数值分析方法。热-结构耦合场的有限元求解方法主要有两种：直接耦合法和间接耦合法。直接耦合法虽然精度较高但其收敛性差，且计算量大，不适用于工程实践应用，而间接耦合法对于温度场和应力场耦合较弱时特别适用，易于收敛，计算简单且精度也能满足工程要求[15]。因此本文在求解断路器瓷套热-结构耦合场时采用间接耦合法。

根据高压断路器瓷套基本结构及其运行状况，建立的瓷套无缺陷有限元仿真模型见图2。为方便有限元的计算分析，所作主要简化包括：瓷套组成部分的材料各向性质具有一致性，忽略材料的热电效应带来的影响[16]。模型设置的边界条件主要包括：重力加速度9.8 m/s2，瓷套腔内SF6气体压力为0.69 MPa，温度热应力参考温度为18 ℃。

图2 高压断路器室瓷套有限元仿真模型Fig.2 Finite element simulation model of highvoltage circuit breaker porcelain bushing

根据本文介绍的瓷套裂纹临界尺寸数值计算方法，裂纹数值建模过程见图3，本文考虑的是表面直缘裂纹。图3(a)为裂纹辅助模型，图3(b)为将裂纹辅助模型移动到无缺陷瓷套模型正前方区域并进行相应的布尔操作后含裂纹的瓷套模型，图3(c)为裂纹区域，图3(d)为含裂纹瓷套模型网格图划分情况。

3 断路器瓷套裂纹临界尺寸计算分析

瓷套在运行过程中所受的静态载荷力主要包括瓷套自身及其金属附件的重力、瓷套腔内SF6气体向外作用压力、温度热应力等，外界环境温度设为-2 ℃，有限元仿真得到的静态载荷力下瓷套的应力分布见图4。瓷套本体材料为脆性陶瓷，易在拉应力作用下发生脆性断裂，而在压应力下则要安全得多[17]，瓷套断裂事故统计也表明断裂一般均由拉应力引起，且发生在瓷套陶瓷本体[18]。因此本文只对瓷套本体拉应力进行分析，瓷套本体的应力分布见图5。

(a) 裂纹辅助模型

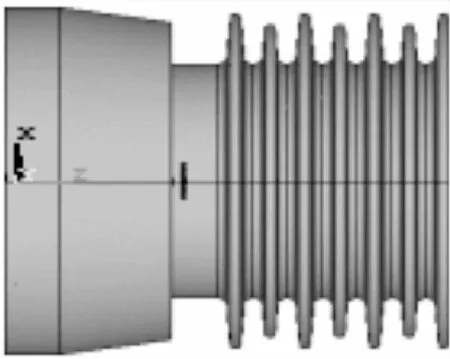
(b) 含裂纹的瓷瓷套模型

(c) 裂纹区域

(d) 含裂纹瓷套网格划分图图3 瓷套裂纹建模Fig.3 The crack modeling of porcelainbushing

图4 断路器瓷套应力分布图Fig.4 The stress distribution of circuit breaker porcelain bushing

图5 瓷套本体应力分布Fig.5 The stress distribution of bulk porcelain bushing

3.1 不同位置下裂纹临界尺寸分析

为分析裂纹位于不同位置时，瓷套裂纹的临界尺寸大小及其变化规律，根据建立的含裂纹瓷套数值模型及裂纹临界尺寸数值法进行相应的计算。图6为裂纹分布位置示意图。裂纹长深比设为常见的4:1，图7为计算得到的θ=180°时裂纹临界裂纹尺寸随L的变化情况，图8为L=100 mm时裂纹临界裂纹尺寸随θ的变化情况。

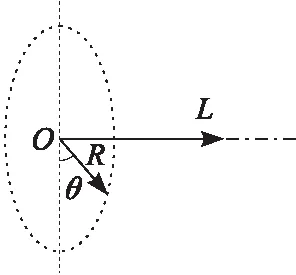
图6 裂纹分布位置示意图Fig.6 The distribution of crack position

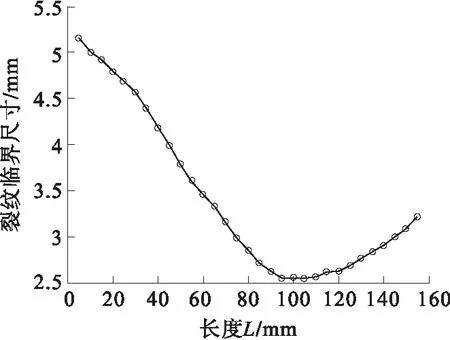
图7 不同L下的临界裂纹尺寸Fig.7 Critical crack size under different L

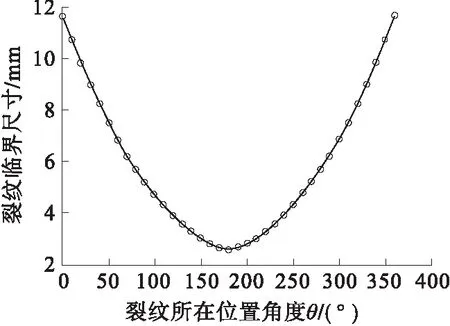
图8 不同角度θ下的裂纹临界尺寸Fig.8 Critical crack size under different position angle θ

由图7可知，当θ=180°时，裂纹临界尺寸会随着其所处长度L先逐渐减小，后逐渐增大，约在h=105 mm处达到最小值2.55 mm。由图8可知，当h=100 mm时，裂纹临界尺寸会随角度θ呈对称分布，θ=180°时值最小，θ与180°相差越远，裂纹临界尺寸越大。

3.2 不同长深比下裂纹临界尺寸分析

瓷套的裂纹形状在实际中是很复杂的，虽以直缘裂纹为主，但其长深比并不固定[19]。为分析裂纹临界尺寸随长深比的变化规律，保持裂纹θ=180°、L=100 mm不变，改变其长深比，计算得到的裂纹临界尺寸的变化规律见图9。由图9可知，裂纹临界尺寸会随着其长深比的增大而逐渐减小，且减小的速度越来越慢，瓷套裂纹临界尺寸主要决定于裂纹深度。

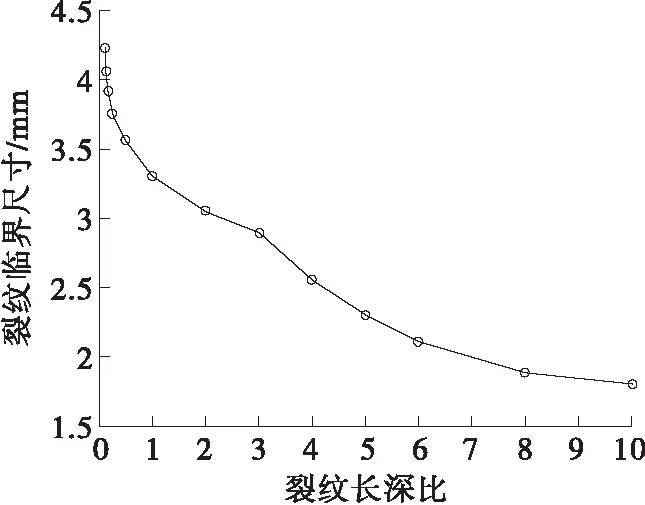
图9 不同长深比下的裂纹临界尺寸Fig.9 Critical crack size under different length-to-depth ratio

3.3 不同弯曲载荷下的裂纹临界尺寸分析

瓷套在运行过程中要受到各种力的综合作用，风载荷、电动力载荷等都可以等效转化为瓷套自由侧的弯曲载荷，因此瓷套在不同运行工况下所受的弯曲载荷大小是不同的[20]，为分析不同载荷下瓷套裂纹临界尺寸的大小及变化规律，设置瓷套裂纹所在位置θ=180°，h=100 mm，长深比为4:1，改变瓷套自由侧向下弯曲载荷的大小，计算得到的不同弯曲载荷下瓷套裂纹临界尺寸见图10。由图10可知，瓷套裂纹临界尺寸的变化与弯曲载荷呈近似反比例关系，瓷套所受弯曲载荷越大，瓷套裂纹临界尺寸则越小。

图10 不同弯曲载荷下的临界裂纹尺寸Fig.10 Critical crack size under different bending loads

4 结论

瓷套裂纹尺寸大于临界值时便会发生断裂故障，给电力系统的安全稳定运行带来严重危害。本文基于应力强度因子的相互积分有限元计算法及三维裂纹实体建模法，结合高压断路器瓷套的基本结构及实际运行情况，建立了瓷套热-结构耦合有限元数值计算模型及裂纹临界尺寸数值计算模型，计算分析了不同位置、不同长深比和不同弯曲载荷下的裂纹临界尺寸大小，结果表明：高压断路器瓷套裂纹的最小临界尺寸在固定侧法兰口最上方位置，裂纹临界尺寸是关于轴线呈前后对称分布的；瓷套裂纹在不同长深比下的临界尺寸是不同的，其尺寸主要决定于裂纹深度；瓷套裂纹临界尺寸随弯曲载荷的增大而减小，两者呈近似反比例关系。本文研究结果可为瓷套无损探伤灵敏度的确定及其运行健康状况的评估提供有效的理论参考和技术支持。