地貌起伏坡度因子对架空输电线路耦合过电压的影响

，

(1.国网安徽省电力有限公司，合肥 230022； 2.国网安徽省电力有限公司淮北供电公司，安徽 淮北 235000)

0 引言

随着社会的飞速发展，输电线路、变电站等电力系统建设也越来越多。根据电网公司输电线路遭受破坏统计数据显示，每年因雷击造成的线路跳闸、闪络等故障事件数占总故障数前列。当雷击输变电杆塔时，产生瞬时变化的电磁场，而电磁场会在输电线上产生耦合过电压。同样，雷击输电线路附近也会在线路上感应幅值较高的过电压[1-4]。因雷击在线路上耦合的过电压会引起线路的跳闸，从而造成断电事故，对电力部门带来不可估量的经济损失。

针对电力部门对电网雷电防护业务的需求，包括雷电监测、线路雷击跳闸、应急抢修等业务在时间、空间上的特点，越来越多的学者对输电线耦合雷电过电压进行了研究。姜伟等[5]针对现有输电线路雷击耦合过电压计算手段的不足，提出了基于DEPACT宏模型的输电线路耦合过电压改进计算方法。指出了该计算方法要优于FDTD算法。李海涛等[6]对规程法雷电耦合过电压计算模型进行改进，主要研究了土壤电阻率、输电线长度等因子对10 kV配电线路耦合过电压的影响。研究得出了线路耦合过电压幅值随着土壤电阻率的增大而减小。向保林等[4]基于FDTD算法对闪电通道任一位置处建立通道回击电流模型，并建立多导线传输的耦合电压计算方法，对输电线路任一位置处雷击过电压进行计算。黄志都等[7]利用ATP-EMTP电磁暂态响应仿真软件，对杆塔进线端线路耐雷水平进行计算。研究指出，输电线三相均安装电涌保护器，能够有效的抑制雷电耦合过电压。刘刚等[8]研究指出，不同地形地貌对雷电流峰值具有较大的影响。还有其余学者也考虑地形地貌因子对雷电流以及过电压影响进行了研究[9-12]。

虽然很多学者采用不同的理论计算模型对输电线路耦合过电压进行了一系列的研究，但从研究过程可以看出，均是假设地面是水平面的情况，忽视了真实环境下地表存在一定坡度的实际情况。因此，为了得到更真实、准确的线路耦合过电压情况，本文利用FDTD算法，考虑地表起伏角度影响因子，对电磁辐射场进行计算，然后结合Agrawal耦合模型对输电线两端点耦合过电压进行计算，研究其差异性。Agrawal耦合模型计算出的耦合过电压精确度已经被人工引雷试验证实[13-14]。因此，本文选用Agrawal耦合模型计算出的雷电过电压所得结果是准确可靠的。

1 计算模型建立

1.1 等效计算模型研究

图1(a)为本文考虑地表起伏坡度的输电线路耦合过电压等效计算模型，在闪电通道电磁辐射计算中，FDTD算法是建立在直角柱坐标下，对于倾斜表面利用FDTD方法不利于对空间网格进行划分。因此，本文图1(a)计算模型进行改进，改进原则为将倾斜表面等效为倾斜通道情况，即主要将斜坡等效为水平面，而原来垂直水平面的闪电通道设置成倾斜放置，倾斜角度与地表起伏角度相一致，见图1(b)。

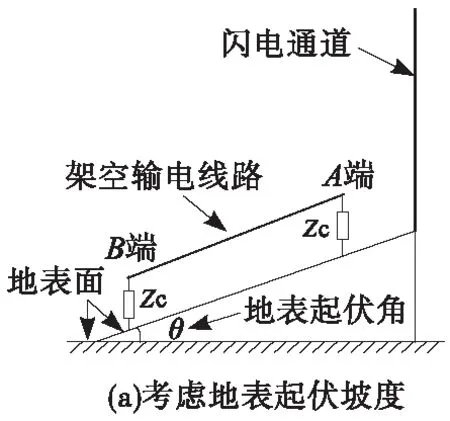
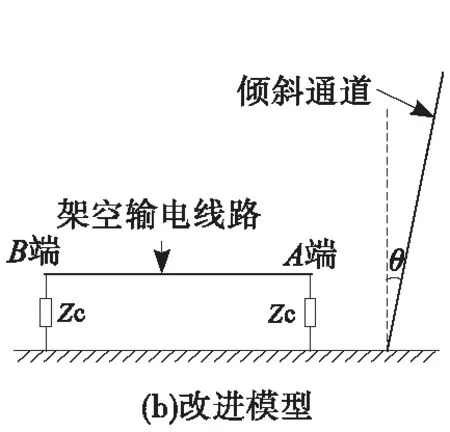
图1 考虑地表起伏坡度的输电线路耦合过电压等效计算模型Fig.1 Equivalent calculation model of transmission line coupled overvoltage considering surface gradient

从图1(b)可看出，倾斜通道不再满足二维柱坐标下轴对称的计算条件，因此需要对通道基部电流源公式在直角坐标系下进行改进。图2为倾斜通道直角坐标系下示意图，I为倾斜通道基部电流，S1为三维直角坐标系下Yee元胞的下表面。Maxwell旋度方程的微分表达式如下：

(1)

根据面积分与环路积分计算公式，对式(1)电场强度、磁场强度、电流密度在S1上进行积分：

(2)

根据S1和S2的关系，对式(2)中电流密度积分表达式进行改写：

(3)

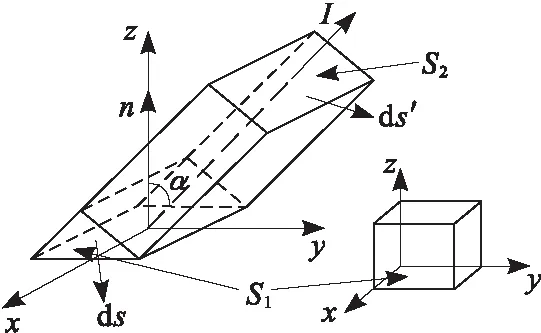
图2 倾斜通道直角坐标系下示意图Fig.2 A schematic diagram in a rectangular coordinate system with an inclined channel

将式(3)代入式(2)，同时对电磁场进行离散差分处理，可以得到Ez离散差分形式：

(4)

同样有：

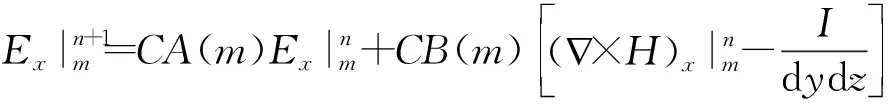
(5)

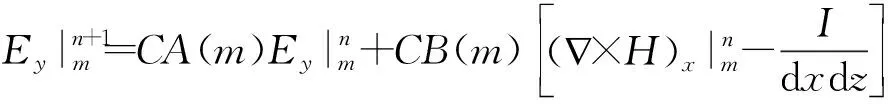
(6)

1.2 输电线路耦合过电压计算模型

利用上述介绍的二维FDTD算法对等效计算模型进行网格划分，计算出不同坡度情况下雷电电磁场变化情况，然后结合Agrawal耦合模型对输电线两端点耦合过电压进行计算。在利用Agrawal耦合模型对过电压计算过程中，由于本文主要研究架空线两端位置处雷击过电压变化趋势，因此仅需要考虑与架空线水平入射的电场水平分量，因为在Agrawal耦合模型中水平电场为雷电感应过电压的激励源。图3为Agrawal耦合过电压计算模型等效电路图，对Maxwell方程组进行回路积分处理，可得到以下表达式：

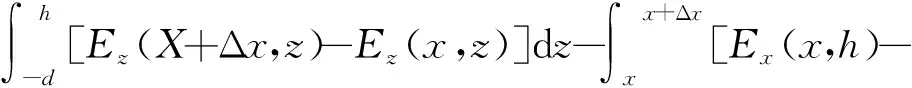
(7)

经过公式推导，可以得出架空线两个端点处耦合过电压计算表达式：

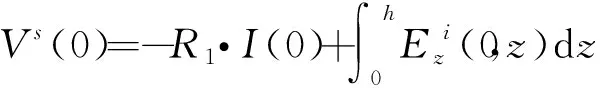
(8)

式中，R1和R2分别为架空线路两端的匹配阻抗，在本文研究中假设架空线两端匹配阻抗相同，图中用Zc表示。

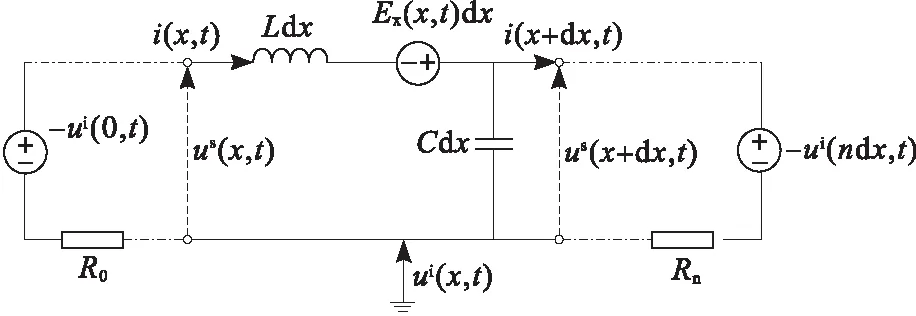
图3 Agrawal耦合过电压计算模型等效电路图Fig.3 Equivalent circuit diagram of Agrawal coupling overvoltage calculation model

2 计算结果分析研究

2.1 算法准确性验证

为了验证本文所建立的架空线路耦合过电压计算模型的准确性，本文假设地表起伏度θ=0°的情况，与研究学者计算结果进行比对。Baba等[15]利用C-R近似算法以及采用Agrawal耦合模型，考虑雷击地面时，对架空线过电压计算研究中，假设闪电回击速度为c/3(m/s)，地面土壤电导率(0.01 S/m)为均匀的情况，闪电通道长度为8 km，架空线距离通道40 m。本文选取参数与该作者一致，计算出耦合过电压与本文对比结果见图4。从图中可以看出，针对地表无起伏坡度，且在相同计算参数设置情况下，本文计算结果与文献[15]具有较好的一致性，虽然在峰值上存在一点偏差，主要是因为文献[15]采用的是C-R近似算法，缺乏FDTD算法对空间区域进行网格划分的优势。因此，本文结果应该是优于Baba结果的。文献[15]中并没有研究地表起伏角度对架空线过电压的影响，本文将基于上述建立的模型，继续研究地表起伏角度在架空线两个端点处过电压的差异性。

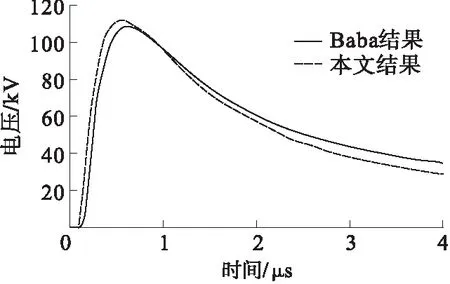
图4 本文计算结果与Baba等结果比对Fig.4 Comparison between the results of this paper and the results of Baba

2.2 地表不同起伏角度对架空线两端过电压影响

为了研究地表起伏角度对架空线两端处耦合过电压的影响，本文假设回击速度v=3/c(m/s)，地面土壤电导率(0.01 S/m)为均匀的情况，闪电通道长度为8 km，架空线长度为1 km，架空线距离斜坡垂直距离为10 m，且架空线与闪电通道之间沿斜坡距离200 m，斜坡角度分别取值θ=0、θ=30°、θ=45°、θ=60°这4种情况。采用上述建立的架空线耦合过电压计算模型，对架空线两个端点处过电压进行计算。图5为靠近闪电通道处架空线起始端过电压随起伏角度变化趋势，从图5中可看出，在不同坡度情况下，架空线起始端耦合过电压存在较大的差异性。地表坡度越大，架空线起始端耦合过电压峰值越大，当地表无坡度，即θ=0时，架空线起始端过电压峰值仅为5.73 kV，θ=60°时，计算出的过电压的峰值为15.44 kV，过电压峰值较水平面增大了2.7倍；θ=30°时计算出的过电压峰值为6.91 kV，过电压峰值与水平面相差较小；θ=45°时计算出的过电压峰值为9.28 kV，过电压峰值较水平面增大了1.6倍。图中还可以看出，随着地表坡度的增加，过电压波形随着时间衰减的过程中，出现了显著的极性反转的情况，陈媛[16]同样指出了在架空线端点处的感应过电压具有双极性的特征。

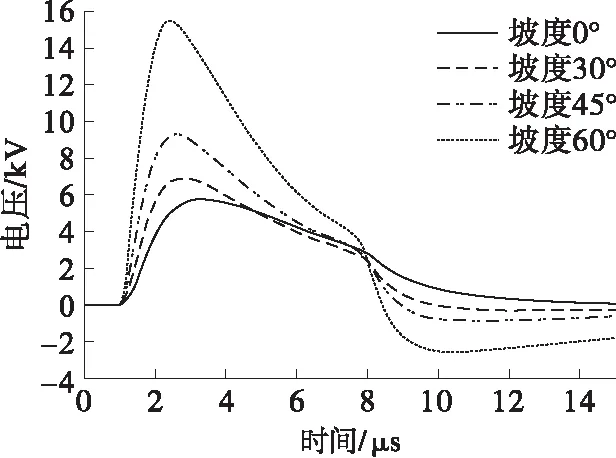
图5 靠近闪电通道处架空线起始端(A端)过电压随起伏角度变化趋势Fig.5 Near the lightning channel overhead at the starting end voltage change with the fluctuation trend of angle

综上分析可以看出，架空线起始端耦合雷电过电压峰值，随着地表坡度的增加而增大，在地表坡度θ>45°时，坡度对架空线起始端过电压影响较大，过电压峰值远远大于地表无坡度情况。同时，坡度越大端点处双极性过电压波形越显著。

图6为架空线末端处过电压随起伏角度变化趋势，从图中可以看出，在不同坡度情况下，架空线末端耦合过电压同样存在一定的差异性。当地表无坡度即θ=0时，架空线末端过电压峰值为1.68 kV，θ=60°时，计算出的过电压峰值为1.98 kV，过电压峰值较水平面增大了0.3 kV；θ=30°、θ=45°时，计算出的过电压峰值分别为1.26 kV、1.28 kV，过电压峰值均小于地表无坡度情况。可以看出，当地表起伏坡度θ>60°时，架空线末端过电压略大于地表无坡度情况。对比图5可看出，在相同坡度情况下，架空线起始端感应过电压峰值远远高于末端处，主要是因为线路存在一定的阻抗，且始末端距离较远，过电压在不断的衰减。

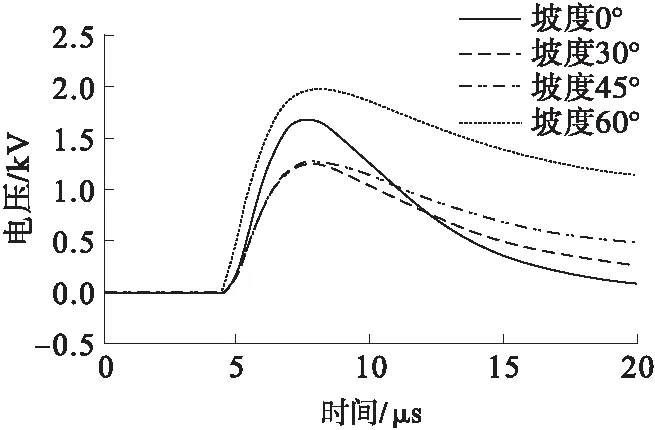
图6 架空线末端(B端)处过电压随起伏角度变化趋势Fig.6 Overhead at the end of over voltage changes with the fluctuation trend of angle

综上分析可以看出，地表坡度对架空线末端感应过电压峰值影响较小，在地表坡度θ>60°时，架空线末端过电压峰值略微高于地表无坡度情况。

3 结论

利用FDTD算法，考虑地表起伏角度影响因子(θ=0、θ=30°、θ=45°、θ=60°)，对电磁辐射场进行计算，然后结合Agrawal耦合模型对输电线两端点耦合过电压进行计算，主要得出了以下结论：本文针对地表无坡度情况计算结果与文献[15]具有较好的一致性，验证了本文的算法；架空线起始端耦合雷电过电压峰值，随着地表坡度的增加而增大，在地表坡度θ>45°时，坡度对架空线起始端过电压影响较大，过电压峰值远远大于地表无坡度情况，坡度越大端点处双极性过电压波形越显著；地表坡度对架空线末端感应过电压峰值影响较小。