上下游双调压室引水发电系统小波动稳定性分析

耿清华

（大唐水电科学技术研究院有限公司，广西 南宁 530029）

小波动稳定是指引水发电系统受到微小扰动后，在调速器和其他控制装置的作用下，经过一定的时间恢复到原来的运行状态或维持在一个新的平衡状态稳定运行。这里指的稳定性仅指引水发电系统的调节过程稳定与否，它不包含机组的振动和摆度等稳定运行指标。水电站在运行过程中，小波动是经常性的，因此分析小波动工况的稳定性显得尤为重要。

由于地形选址因素的影响，有的水电站需要设计为地下厂房，使水电站的引水隧洞和尾水隧洞都比较长。在这种情况下，常常采用设置上游调压室和下调压室的方法来对引水发电系统进行平压。

目前，已建成的具有上下游双调压室的水电站较少，对上下游双调压室引水发电系统小波动水力过渡过程的研究也不多。文献[1]对上下游双调压室断面面积的计算方法进行了推导，在机组转动惯量、水轮机力矩、调压室面积一定的情况下，对调速器参数变化对小波动的稳定性进行了分析。文献[2]采用大型动力系统的理论推求了上下游双调压室系统水位波动稳定公式，并用实例计算验证了其计算结果的有效性。

1 上下游双调压室引水系统数学模型

1.1 基本假设

小波动稳定性分析中，基本假设[4]如下：1）假定水轮机的转速、水头和导叶开度不变，为线性关系；2）电压波动微小，可以忽略不考虑；3）机组不联网，孤立运行；4）忽略负荷的自调节系数；5）调速器永态转差系数为0。

2.2 数学模型

具有上下游双调压室引水发电系统的示意图见图1。

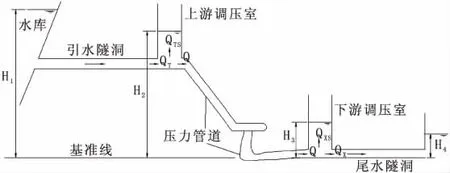
图1 上下游双调压室引水系统示意图

具有长引水隧洞的引水式水电站，主要由水库、引水隧洞、调压室、压力管道、蜗壳、水轮机组、尾水管等组成。在小波动工况下，可以不考虑水体和管壁的弹性，采用刚性水锤理论[3]来分析引水系统的非恒定流。

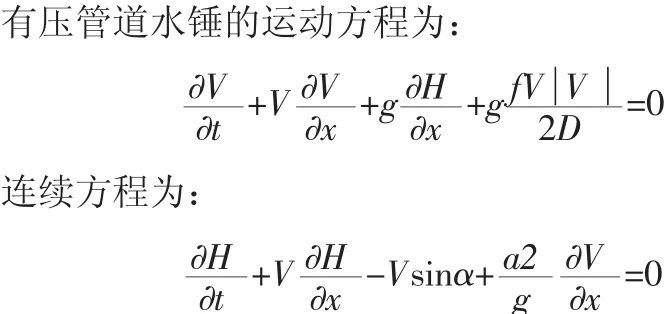
式中：A为过水断面面积；α为管道中心线与水平线的夹角；g为重力加速度；V为AB断面平均流速；x为从管段左端起的距离；H为测压管水头；f为沿程水头损失系数；D为管道内径；t为时间；a为水锤波速。

正特征线方程：

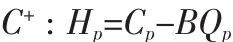
负特征线方程：

特征线方程式中：

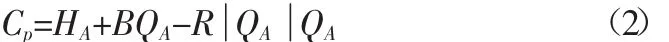
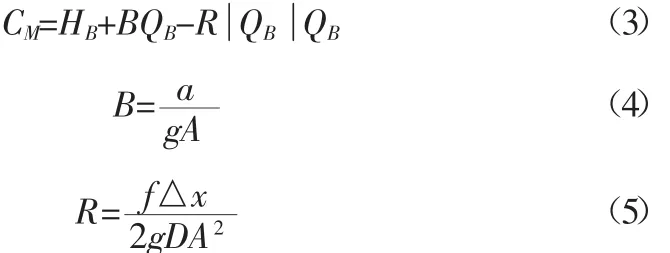
HA为t-△t时刻管段第i-1节点处的水头；

QA为t-△t时刻管段第i-1节点处的流量；

HB为t-△t时刻管段第i+1节点处的水头；

QB为t-△t时刻管段第i+1节点处的流量；

△x为相邻两节点距离；R为阻力系数；CP、CM与t-△t时刻的水头和流量有关，对于时刻t为已知量。

（1）上游水库边界条件

上游水库边界方程为

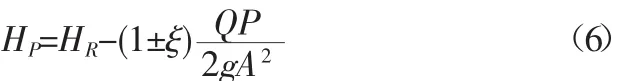
式中：ξ为进口阻力水头损失系数。当水流向下游流动时取“+”，水流向上游流动时取“-”。对进水口处有负特征方程C-，由方程（1）可求出QP，即将上式带入（6）即可得到HP。

（2）调压室边界条件

考虑到水进入调压室的水头损失，得：

式中：QS1为流入上游调压室的流量；Z1为上游调压室的水位；k1为水流流入上游调压室时的水头局部损失系数，流出与流入取值不同；F1为上游调压室的断面积。下标1和2分别表示隧洞和管道的参数。

（3）水轮机边界条件

水轮机工作水头和流量满足的条件为：

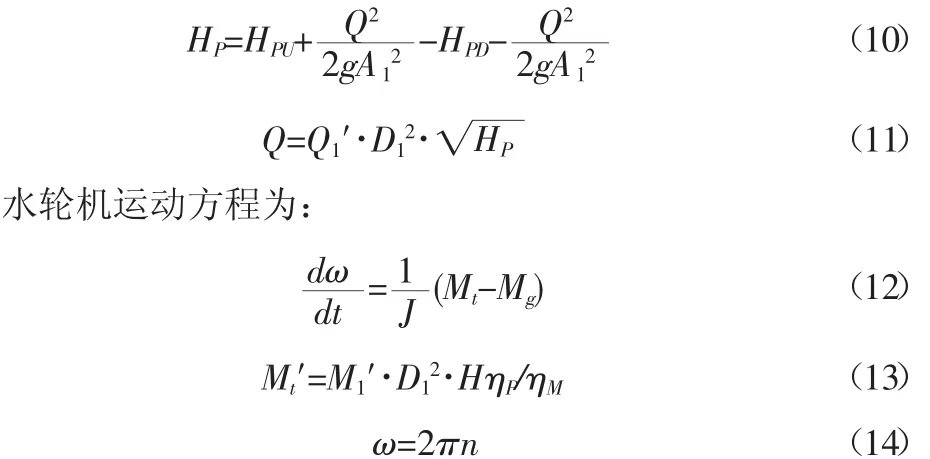
式中：HPU为水轮机进口断面水头；HPD为水轮机出口断面水头；QP为水轮机过渡状态时引用流量；Mt为过渡状态水轮机动力矩；Mg为发电机阻力矩；ω为过渡状态时水轮机旋转角速度；n为过渡状态时水轮机转速；Q1′为过渡状态时单位流量；J为机组总转动惯量。

下标1表示与压力钢管相关的参量，下标2表示与尾水管相关的参量。

联立上述各式，能求解出水轮机过渡过程中的水头和转速值。

（4）尾水隧洞边界条件

不忽略尾水管出口处的局部水头损失时，下游河道边界方程可写成以下形式：

式中：α为尾水隧洞出口局部水头损失系数。

由以上两式可求解尾水隧洞出口节点的压头和流量。

（5）调速器主要方程

调速器采用下列传递函数：

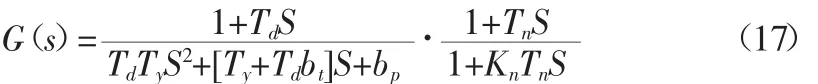
式中：Ty为导叶接力器反应时间；Td为调速器缓冲时间常数；bt为调速器暂态转差系数；y为导叶接力器行程的相对值；σ为主配压阀行程的相对值；Tn为调速器微分时间常数；Kn为比例系数；ξ为暂态反馈输出相对偏差；x为转速相对偏差；γ输出相对偏差。

3 实例计算

3.1 工程概况

BL水电站引水隧洞长度6902.66 m，内径11.0 m，采用全断面钢筋混凝土衬砌。钢筋混凝土衬砌最大糙率0.016，最小糙率0.012，平均糙率0.014。压力管道内径5.3 m，1#压力管道长为519.064 m，2#压力管道长为504.067 m，3#压力管道长为499.832 m，钢管糙率0.012。局部水头损失系数按照引水系统布置确定。上游调压室为长廊形阻抗式，初拟阻抗孔口直径3.0 m，调压室设计净面积737.10 m2。下游尾水调压室也为长廊形阻抗式，初拟阻抗孔口直径3.2 m，下游尾水调压室设计净面积600.40 m2。水库正常蓄水位为2920.00 m，水库非常运用洪水位为2922.71 m，水库死水位为2918.00 m，厂房正常尾水位为2689.01 m，厂房最低尾水位为2687.06 m，正常运用洪水位为2694.44 m，非常运用洪水位为2694.97 m。

3.2 小波动稳定计算

根据BL水电站的引水发电系统的参数，计算的上游调压室临界稳定断面积288.43 m2，尾水调压室临界稳定断面积247.83 m2。在正常蓄水位不变与负荷波动5%的工况下，选取了4组不同的上下游调压室断面积。按照托马稳定条件，对上下游调压室不同水位变化进行小波动稳定的计算，计算结果分别见表1、表2和图2～图6（图中（a）上游调压室和（b）下游调压室）。

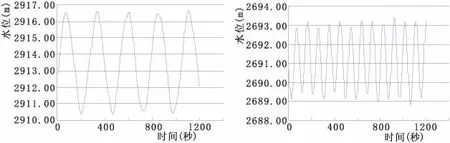
图2 上游调压室面积230.00 m2，下游调压室面积110.00 m2

表1 正常蓄水位2920.00 m下不同调压室断面积小波动计算转速结果

表2 正常蓄水位2920.00m下不同调压室断面积小波动计算水位结果

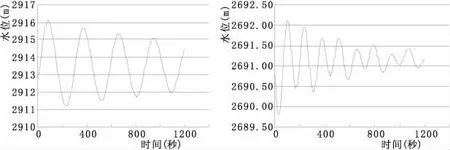
图3 上游调压室面积288.43 m2，下游调压室面积247.83 m2

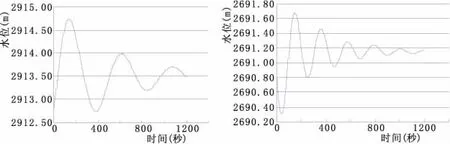
图4 上游调压室面积737.10 m2，下游调压室面积600.40 m2

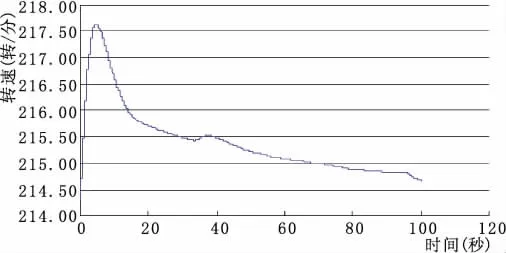
图5 上游调压室面积288.43 m2，下游调压室面积247.83 m2，转速变化

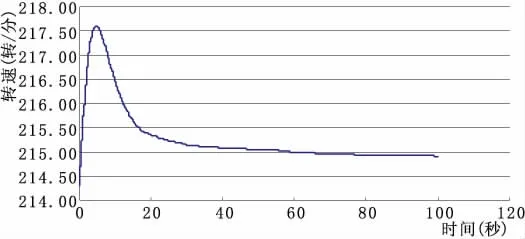
图6 上游调压室面积737.10 m2，下游调压室面积600.40 m2，转速变化

据图2～图6分析可知：调压室选取比托马稳定断面稍小的断面积，引水发电系统也能稳定。当上游调压室断面积小到230 m2，下游调压室断面积小到110 m2左右时，引水发电系统开始变得不稳定，上下游调压室内水位波动发散。当上下游调压室断面积为计算的临界稳定断面积时，引水发电系统是稳定的，转速最大超调量为1.55%，±0.4%调节时间为53.92秒，上游调压室水位波动衰减率为1.00014，下游调压室水位波动衰减率为1.00006。此时引水发电系统小波动是稳定的，但调节时间较长，衰减较慢，调节品质不佳；当上下游调压室断面积分别取设计值时，转速最大超调量为1.54%，±0.4%调节时间为30.26秒，上游调压室水位波动衰减率为1.00026，下游调压室水位波动衰减率为1.00008。此时引水发电系统小波动稳定，调节时间较短，衰减率较大，调节品质较好；当上下游调压室面积进一步增大时，调节时间并没有显著降低，衰减率也基本没有变化，调节品质并没有显著的提高。

4 结语

（1）设计具有上下游双调压室系统的水电站，应考虑引水系统小波动稳定性对调压室截面积的要求。通常情况下，上下游调压室的稳定要求总截面积会大于单一上游调压室和单一下游调压室的稳定要求面积之和。

（2）具有上下游双调压室的引水发电系统，在甩负荷工况下，上游调压室水位先升高，同时尾水调压室内水位先下降，之后以各自的波动周期波动。相应的，在增负荷工况下，上游调压室水位先降低，同时尾水调压室水位先升高，之后以各自的波动周期波动。具有上下游双调压室的引水发电系统，上下游调压室的波动周期必须避免波动周期相近，以免发生共振现象。

（3）具有上下游双调压室的引水发电系统，调压室的稳定断面比单一调压室系统调压室断面大。实际上，双调压室系统的调压室断面采用比理论推导的稳定断面小的面积，引水发电系统也可能是趋向稳定的，但是调节品质往往不够理想，必须通过多方案的过渡过程计算，结合经济分析，得出合理的调压室断面积。

（4）采用解析公式计算的上下游调压室水位波动周期与采用过渡过程电算方法计算的水位波动周期基本一致，水电站水力过渡过程计算方法和常用边界数学模型同样适用于具有上下游双调压室系统的水电站。