复杂微通道内气泡在浮力作用下上升行为的格子Boltzmann方法模拟∗

2018-12-14娄钦李涛杨茉

物理学报 2018年23期

娄钦李涛杨茉

(上海理工大学能源与动力工程学院,上海 200093)

(2018年7月6日收到;2018年9月2日收到修改稿)

1 引言

气液两相流中的气泡在浮力作用下的上升行为广泛存在于自然界和生物、化学、工业加工等工程应用中,如:沸腾现象,气泡在流化床系统内的形成、变形及运动现象[1],医学领域中微气泡所产生的动力学行为导致的声致穿孔现象[2],在冶金领域因化学反应而导致的气泡形成、长大、运动现象[3],微生物驱油过程中气泡的产生、变形和移动现象[4],热交换器中气泡和液滴的传热传质过程[5]等.因此,开展微通道内气泡上升行为的研究具有重要的现实意义.

近几十年来,许多学者对微通道内的气泡运动特性进行了实验以及数值研究.早期的研究大都关注气泡在光滑壁面微通道内的运动行为.Bhagat等[6]通过实验考察了高莫顿数下气泡在黏性流体中上升时形状和终端速度的变化,并发现当雷诺数小于110时气泡后部的流线为封闭形态,而当雷诺数大于110时气泡的运动呈现不稳定状态,后部的流线出现开放形态.Weber等[7]在此基础上,进一步研究了不同雷诺数下上升气泡的尾部流线轨迹.为了进一步刻画气泡上升过程中的运动特性,Hua等[8]应用波前追踪法(front tracking)研究了高雷诺数、高密度比和高黏性比情况下,气泡在黏性流体中的平均上升速度、形状等特性,并将气泡的终端速度和终端形状与实验数据进行对比,发现气泡上升速度近似呈对数形式增长.艾旭鹏等[9]基于边界层理论,采用边界积分法,研究了流体黏性效应和表面张力对气泡运动特性的影响,发现流体黏性会使气泡振动幅值衰减,表面张力的增加会缩短气泡脉动周期,并提高势能.Maxworthyt等[10]考查了多个气泡在浮力作用下的运动特性,并给出了不同莫顿数下气泡群在上升过程中的阻力系数和雷诺数之间的关系.Rensen等[11]调查了气泡群在不同上升速度时的形状变化,发现水箱内水的深度基本不影响气泡群的整体形状.Takada等[12]采用格子Boltzmann自由能模型研究了初始垂直放置的两个气泡的变形情况和内部流线图.除了管道内的流线轨迹以及气泡形状、速度等宏观特性,还有学者研究了气泡运动过程中界面的动力学行为.Sussman等[13]应用Level set方法,研究了单个气泡上升过程中的界面形变以及破裂现象,发现随着表面张力和黏性比的增加,气泡越不容易发生变形和破裂现象,随着雷诺数的增加,气泡的变形会越来越剧烈.Baltussen等[14]采用流体体积函数(volume of f l uid,VOF)方法,考察了不同爱特威数下气泡上升过程中界面的变化,发现当爱特威数小于1时,气泡上升过程中基本不发生形变.以上文献主要研究了气泡初始位置在管道中间时的情形.Fakhari等[15]基于格子Boltzmann自由能模型,研究了气泡初始紧贴壁面,并沿壁面上升的情况,发现在高爱特威数下,气泡变形加剧,并且在足够高的阿基米德数和低莫顿数时会出现气泡破裂的情况.

对竖直光滑通道内气泡上升过程中的分裂、合并等现象及其运动路径、速度流场已经有了广泛的研究,为了研究气泡在复杂管道内的运动特性,Uchiyama等[16]通过实验考察了气泡群绕竖直通道中心单个圆柱障碍物上升的运动状况,得到了气泡群演化过程中的速度场和绕圆柱障碍物后的运动形状.Salcedo等[17]研究了通道内有两个相同的圆形障碍物时雷诺数对气泡形状和速度的影响.Li等[18]研究了单个气泡绕圆形障碍物上升时表面张力和浮力的变化对气泡形状的影响.Alizadeh等[19]考察了通道内圆形障碍物尺寸和数量对单个气泡运动特性的影响.除了气泡在浮力作用下的上升行为,Yi等[20]采用格子Boltzmann自由能模型研究了压力驱动下气泡在含方形障碍物的微通道内的上升问题,主要考察了三种特定的壁面润湿性(接触角θ=60◦,90◦,120◦)以及不同的气泡初始位置对气泡形状和终端速度的影响.

以上研究工作推动并揭示了气泡运动过程中的一些运动机理,然而还不够深入,例如微通道表面润湿性对气泡的动力学行为影响较大,但现有文献对壁面润湿性的范围考虑不够全面.其次,如工业上换热器微气泡强化换热技术[21]中通道的表面都不是光滑的,而目前针对壁面上障碍物对气泡运动特性影响的研究非常少.此外,尽管已有研究考虑了气泡运动过程中的变形、破裂现象,但其内部机理尚不清晰,并且气泡和固体壁面的相互作用以及气泡穿过通道后的剩余质量也鲜有报道.鉴于此,本文采用格子Boltzmann方法(lattice Boltzmann method,LBM),主要针对气泡经过换热器圆形管束的上升问题,研究气泡在含有半圆形障碍物微通道内的界面动力学行为以及宏观运动特性,主要考察障碍物表面润湿性、浮力大小、障碍物尺寸和气泡初始位置对气泡在复杂微通道内受浮力上升问题的影响,探究气泡变形、分裂等动力学行为以及气泡运动的剩余质量、上升速度和终端速度.

2 数值方法

2.1 格子Boltzmann模型

LBM在模拟气液两相流时有一些独特优势,例如可以直观描述流体和流体之间以及流体和壁面之间的相互作用、不需要追踪相界面、边界条件易于处理,因此该方法近几年受到学者们的广泛关注并得到迅速发展.目前,基于不同相互作用力的处理方式,已提出多种气液两相流模型,主要有颜色模型[22]、伪势模型[23,24]、自由能模型[25,26]、基于Enskog理论和相场理论的模型[27,28].以上模型都成功地用于研究气液两相流动问题.在本文中采用He等[29]基于Enskog理论提出的LBM研究复杂微通道内的气泡上升问题.

He等[29]提出的两相流格子Boltzmann模型采用两个分布函数,fα和gα分别描述指标参数和速度/压力的演化过程,可以提高数值稳定性.由于该模型已在文献[29]中有了详细的介绍,故本文只做简要的描述.在此模型中,分布函数fα和gα分别为

式中 α=0,1,2,···b−1,b为离散速度方向个数;x和t分别表示位置和时间;τ代表松弛时间,与运动黏度ν相对应的关系为代表时间步长,是与格子速度c=dx/dt相关的常数);ϕ,ρ,u分别代表指标函数、流体密度和流体速度;κ代表表面张力强度系数;G为体积力;其中p为流体压力,演化方程中ψ(ϕ)依赖于模型中用的状态方程,本文中采用Carnahan-Starling状态方程[30],对应的ψ(ϕ)为

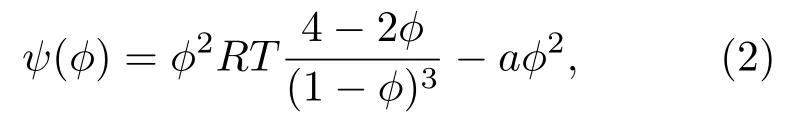
其中a决定分子间相互吸引力强度,R为气体常数,T为流体温度.在方程(1)中,函数Γα(u)表达式为

其中ωα代表权重系数.演化方程中(x,t)和(x,t)是分布函数对应的平衡态,其形式如下:

宏观量指标参数ϕ,压力p以及速度u的统计由下面方程给出:

流体密度ρ(ϕ)可由指标参数ϕ计算得到,

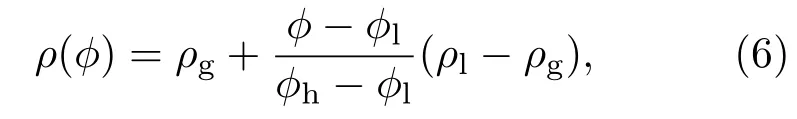
其中 ρg和ρl分别代表气相流体和液相流体密度;ϕh和ϕl为指标参数的最大值和最小值,可由Maxwell重构得到.采用Chapmann-Enskog多尺度展开可以得到方程(1)对应的宏观动力学方程[31]:

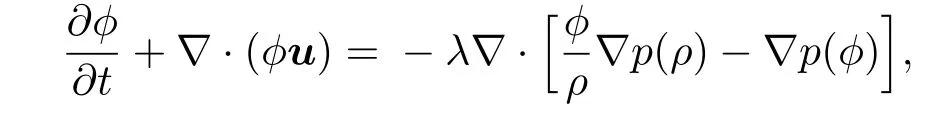
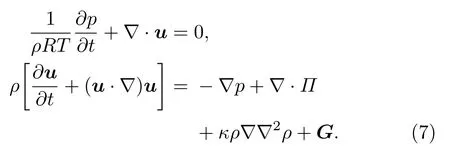
本文使用D2Q9模型来进行数值模拟研究,权重系数ωα设置为:当α=0时,当α =1—4时,当α =5—8时,eα为离散速度,表达式为

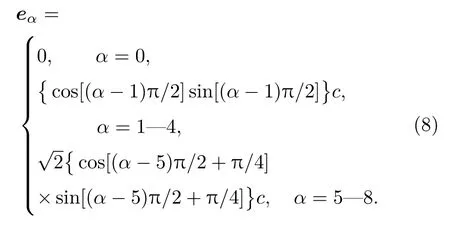
关于梯度和拉普拉斯算子的离散方法采用二阶中心各向同性方法(ICS)[32]:

2.2 润湿性处理

壁面润湿性反映流体和固体之间相互作用力的强度.在微通道内,润湿性是影响气液两相动态行为的重要参数.在LBM中,壁面的润湿性通过边界条件来描述.本文将考虑润湿性对气泡通过障碍物通道的动态影响,润湿性边界条件采用Davies等提出的方法[33],在该方法中采用表面亲和性αs刻画壁面的润湿强度,并把表面亲和性与指标参数ϕ联系起来,其关系式为

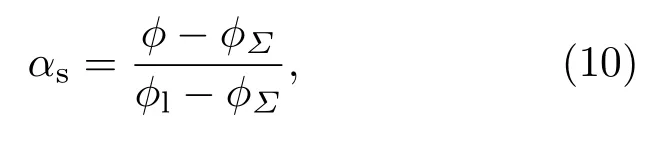
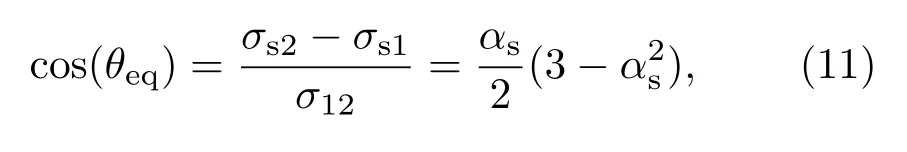
其中σs1,σs2分别代表固-液表面张力和固-气表面张力;σ12为气-液表面张力.

3 模型验证

3.1 拉普拉斯定律

首先采用Laplace定律来验证模型的正确性.初始时在Lx×Ly区域中心内放置半径为R,密度为ρl的静止圆形液滴,其余区域充满密度为ρg的气体.根据Laplace定律可知,当系统达到稳定时表面张力σ恒定,且液滴内外的压力差∆P与半径的倒数1/R呈线性关系,关系式为

本文的验证中,初始液滴半径R分别取24,28,32,36,40五种情况,并考虑不同表面张力强度κ=0.1,0.15,0.2,以保证验证可信度.在数值模拟中网格数均取为128×128,状态方程中分子间强度a为4.0,RT的取值为1/3,对应的ϕh和ϕl分别为0.250291和0.022838,其余参数设置为:ρl=0.5,ρg=0.1,ν=1/6.计算域四周的边界条件皆为周期性边界条件.数值模拟达到稳态的条件为

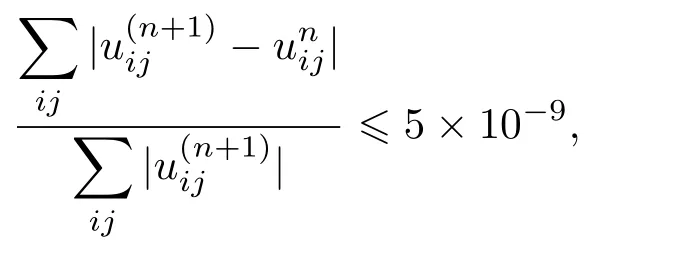
图1 液滴内外压力差pi−po和半径倒数1/R之间的关系Fig.1 . Relationship between pressure jump across the droplet interface pi−p0and inverse of droplet radius 1/R.

3.2 气泡在光滑壁面管道内的上升行为

气泡在光滑壁面通道内受浮力上升的问题与本文所要研究的问题较贴近,且已有学者对该问题进行了大量研究,因此本章节将采用该算例验证模型的正确性.对于该问题,初始时在Lx×Ly的计算区域内放置半径为R密度为ρg的静止圆形气泡,气泡的圆心设为(xc,yc),其余区域充满密度为ρl的液体,在竖直方向施加浮力G=(ρ−ρl)g,其中g为重力加速度.在数值模拟中,Lx×Ly=80×300,R=10,ρl=1.48,ρg=0.52,κ =0.15,xc为微通道水平方向的中心位置,yc为通道高度的1/4,计算域的边界条件设置为:左右固体壁面采用无滑移边界条件,进出口选用周期性边界条件.

该问题有两个重要无量纲数,Eötvös数(Eo)和Morton数(Mo),其中Eo=g(ρl−ρg)d2/σ代表浮力与表面张力的比值;Mo=g(ρl− ρg)µ4l/ρ2lσ3代表黏性力和表面张力的比值,式中d为气泡直径,µl为液体的动力黏度.表1给出了不同Eo数和Mo数时气泡的终端速度Ut,并与LBM方法中基于Enskog理论和相场理论的模型[19]以及VOF方法[34]进行对比,发现结果基本一致.

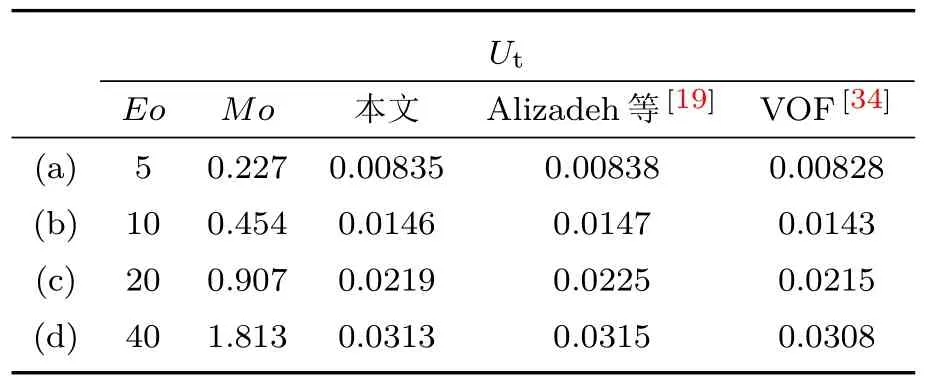
表1 不同模型对应的气泡终端速度Table 1 .Terminal velocities of the bubble obtained by dif f erent models.

图2给出了表1中当Eo=10,Mo=0.4535以及Eo=40,Mo=1.813(对应(b),(d)两种情况)时对应的气泡上升的速度变化趋势,并与Alizadeh等[19]的数据进行对比.从图2中可以看出,本文得到的速度变化趋势与Alizadeh等得到的结果基本一致.具体地说,当Eo数较小时(Eo=10),演化初期气泡速度在浮力作用下迅速增加,随着浮力、表面张力以及黏性力达到平衡,气泡速度基本稳定.当Eo数较大时(Eo=40),演化初期气泡上升速度的增加速率更快,达到的极值更大.当气泡上升速度达到最大值时,由于气泡变形更加明显,因此会在表面张力的作用下,出现速度值略微下降的现象[19],此后各项力之间达到平衡,气泡上升速度近似不变.

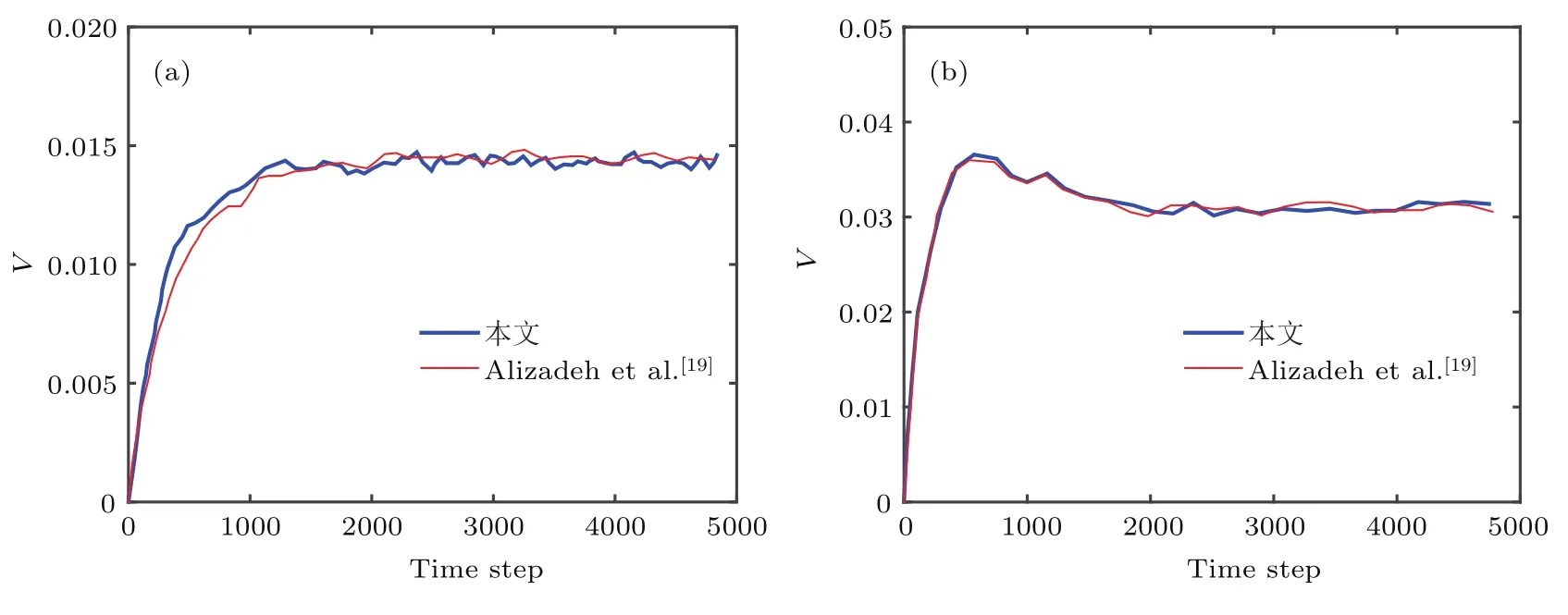
图2 由本文和Alizadeh等(文献[19])得到的气泡上升速度 (a)Eo=10;(b)Eo=40Fig.2 .Bubble rising velocities obtained by the present study and by Alizadeh et al.(Ref.[19]):(a)Eo=10;(b)Eo=40.

图3 不同条件下气泡到达微通道终端时的形状 (a)Eo=5;(b)Eo=10;(c)Eo=20;(d)Eo=40Fig.3 .Bubble shapes at the micro-channel terminal under dif f erent conditions:(a)Eo=5;(b)Eo=10;(c)Eo=20;(d)Eo=40.

为了进一步验证本文模型,图3展示了不同Eo数下,气泡到达通道终端时的形状.从图3中可以看出,当Eo=5时,气泡上升过程中基本保持初始圆形,而随着Eo数的增加,气泡在上升过程中会出现更加明显的形变.此现象与文献[12,35]得到的结果一致.

4 物理问题描述

本文研究的物理问题如图4所示.微通道宽度和高度分别为Lx和Ly,微通道内黑色半圆区域代表障碍物,其半径为R1,蓝色圆形区域为初始在通道内的气泡,其密度为ρg,半径为R2,圆心为(xc,yc),其中xc为微通道水平方向的中心位置,yc为通道高度的五分之一,其余白色区域充满密度为ρl的液体.在流体流动的y方向施加浮力G=(ρ−ρl)g.该问题采用的边界条件与3.2节相同.

图4 模拟问题示意图Fig.4 . illustration of simulation problem.

在下文分析中,为了说明气泡的运动特性,引入两个参数:剩余质量百分比Rq和t时刻气泡在y方向的上升速度vb(t).剩余质量百分比为到达微通道终端的气泡质量占初始气体质量的百分比,这里需要指出的是到达微通道终端的气泡质量即剩余气泡质量可以由初始气泡总质量减去残留在障碍物表面的气相质量得到,也可由气泡穿过障碍物到达微通道终端时所占据的气相区密度求和得到,其中气相区为密度ρ小于0.5·(ρl+ρg)的区域;而t时刻气泡上升√速度定义为气泡竖直方向的上升速度其中x代表t时刻被气泡占据的格点位置,v(x,t)代表t时刻气泡在x点垂直方向上的速度,N代表此时刻被气泡占据的所有格点数.在本文中取为特征时间对时间进行无量纲化,在下文中无量纲时间用T表示.

5 数值结果与分析

5.1 润湿性的影响

本小节主要研究障碍物表面润湿性不同时的气泡运动特性.数值模拟中分别考虑接触角θ=30◦,40◦,50◦,60◦,70◦,80◦,82◦,85◦,90◦,100◦,110◦,120◦,130◦,140◦,150◦的情况,其他参数设置如下:Lx和Ly分别设置为160和600格子单位,Eo=10,Mo=0.4535,R1=60,R2=32,ρl=0.5,ρg=0.1,µl=0.05.

图5给出了接触角θ=60◦时气泡上升速度演化图和对应速度极值的气泡运动瞬时图.从图5中可以看出,在气泡的运动过程中,速度呈波浪形变化,依次出现增加-减小-增加-减小-增加-减小-基本不变几个阶段(与文献[20]中气泡穿过方形障碍物通道时得到的结果类似),对应两个极小值和三个极大值,这些速度极值点均发生在气泡穿过通道较窄部分的过程中.具体而言,演化过程初期,在浮力作用下,气泡速度逐渐增加,在T=1.40时,气泡靠近障碍物表面,通道截面积减小,气泡运动受到阻碍,其速度开始减小.速度减小趋势一直持续到T=3.76,此时气泡顶部刚刚穿过通道最窄部分,随后气泡受到的阻碍力减小,气泡上升速度开始增加.在T=6.86时,气泡底部也穿过了通道最窄部分,随着通道截面积的增加,气泡在表面张力作用下变形,气泡上升速度开始减小,直至气泡前端接近球形(此时T=7.82),之后气泡形状变化不明显,其速度在浮力作用下增加,而在T=8.70时,气泡与障碍物脱离(速度对应第三个极大值).由于气泡脱离障碍物时,与障碍物表面接触部分生成两个较长的“小触须”,发生严重变形,导致气泡与障碍物脱离之后在表面张力作用下收缩,其速度出现下降趋势.随着气泡形状变化越来越小,气泡上升速度趋于稳定(T=11.43之后),此情况与文献[8]中气泡受浮力上升、速度最终会趋于稳定的情况类似.

图5 接触角θ=60◦时对应的气泡上升速度演化图和运动瞬时图Fig.5 .Time histories of the bubble velocity and the snapshots of the bubble at extreme positions under θ =60◦.

与气泡的速度轨迹对应,其形状也发生了巨大的变化.由于浮力的作用,初始圆形气泡在上升速度出现第一次极大值时变成了下凹的球冠形.此时气泡除了受到向上的浮力作用外,还受到障碍物的挤压力,因此气泡发生变形以穿过通道较窄部分.气泡在穿过通道较窄部分过程中,由于障碍物表面亲水而疏气,与障碍物表面始终存在明显的间隔,并且在穿过通道时与障碍物表面接触面积较少.一旦大部分气泡穿过障碍物之间的通道,即快速与半圆形障碍物脱离,恢复成下凹的球冠形稳定上升.

为了进一步说明气泡通道障碍物表面润湿性对气泡动力学行为的影响,图6给出了障碍物表面接触角为120◦的气泡上升速度演化图和对应速度极值的运动瞬时图.对比图5和图6可以发现,当障碍物表面润湿性不同时,气泡上升速度都呈波浪形变化,速度极值点均出现在气泡通过障碍物的过程中,而且在气泡接触障碍物之前,不同时刻气泡上升速度的值基本一致.因此,这两种情况下,气泡都是在T=3.76时刻挤入通道最窄处.然而,随着障碍物表面接触角增加,其对气泡的黏附力增加,气泡通过障碍物通道的上升速度减小,所需要的时间增加.例如,障碍物表面接触角θ=120◦的工况下,气泡从开始挤入通道最窄处到穿过障碍物通道的时间为T=3.76至T=8.55,比θ=60◦时增加了17.98%;气泡由障碍物上部到完全脱离障碍物表面的时间为T=8.55到T=11.06,比θ=60◦时增加了185.22%.完全脱离后的气泡上升速度变化趋势与θ=60◦的情况类似,都是先因气泡形状发生较大的变化,对应的速度有所下降,再随着气泡形状变化越来越小,气泡上升速度趋于稳定.气泡到达微通道终端的总时间T=17.70,相比于θ=60◦的情况增加了14.34%.

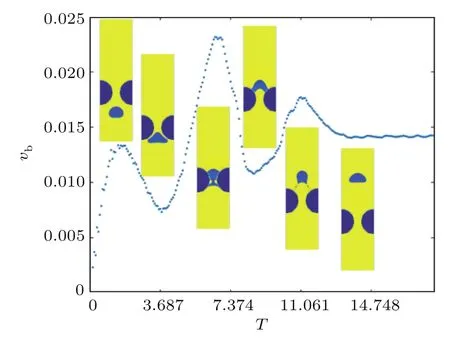
图6 接触角θ=120◦时对应的气泡上升速度演化图和运动瞬时图Fig.6 .Time histories of the bubble velocity and the snapshots of the bubble at extreme positions under θ =120◦.

从以上结果可以看出,随着接触角的增加,障碍物对气泡的黏附力增加,于是气泡穿过障碍物通道所需要的时间更长,困难性增加,有可能造成到达通道终端的速度减小.为了验证这一理论预测,图7给出了气泡终端速度和通道内障碍物表面润湿性之间的关系.从图7中可以看出,随着障碍物表面接触角增加,气泡的终端速度减小,该结果验证了理论预测.

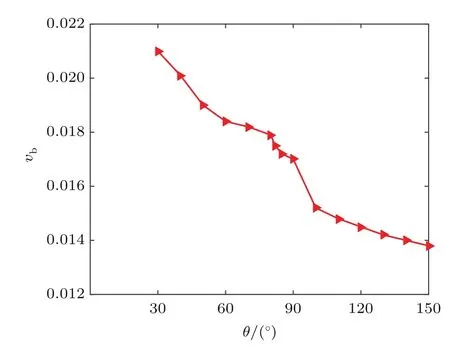
图7 不同接触角下气泡终端速度Fig.7 .Terminal velocities of the bubble under dif f erent values of contact angle.

此外,对比图5和图6还可以发现,当接触角较大时,由于障碍物对气泡的黏附力增加,气泡在通过障碍物之间的通道时,与障碍物表面基本贴合,气泡形状变化出现较大不同.例如,在障碍物表面接触角θ=120◦时,气泡底部通过通道最窄部分时变形严重,底部两侧分别出现小圆孔;气泡整体通过障碍物通道并将要脱离障碍物表面时,其底部被拉伸,出现“拱门”形状.为了更清晰地说明障碍物表面润湿性对气泡形状的影响,图8给出了障碍物表面接触角为150◦时的气泡运动瞬时图.从图8中可以看出,由于接触角的进一步增加,气泡受到的黏附力增大,在通过障碍物之间的通道时,其两侧与障碍物表面完全接触,孔隙消失;在气泡脱离障碍物过程中,其“拱门”形状向两边拉伸更明显.对比图5、图6和图8可以发现,随着障碍物表面接触角的增加,气泡完全脱离障碍物后剩余的质量更少,说明有部分气泡残留在通道障碍物表面上.

图8 接触角θ=150◦时对应的气泡运动瞬时图(从左到右T=3.61,6.49,8.92,12.09)Fig.8 .Snapshots of the bubble at θ =150◦ (from left to right T=3.61,6.49,8.92,12.09).

为了定性刻画障碍物表面润湿性对气泡运动剩余质量的影响,图9给出了不同接触角时气泡剩余质量百分比Rq.从图9中可以看出,当障碍物表面接触角θ小于或等于82◦时,气泡的剩余质量百分比Rq均为100%,说明气泡上升过程中虽然变形严重,但由于障碍物表面疏气,气泡不会黏附在障碍物表面上,而是完整地到达微通道终端.而当障碍物表面接触角θ等于85◦时,如图9中气泡运动瞬时图所示,在气泡通过障碍物通道时,与障碍物表面两侧紧密接触,并受到黏附力作用,部分残留在障碍物表面上,气泡剩余质量百分比为87.37%.随着障碍物表面接触角越来越大,其对气泡的黏附力增大,则残留在障碍物表面上的气泡质量越多,气泡剩余质量百分比Rq明显下降.

图9 不同接触角下气泡剩余质量百分比Fig.9 .Percentage of the bubble residual mass under dif f erent values of contact angle.

5.2 浮力的影响

浮力作为驱使气泡在微通道内上升的作用力,具有重要的研究意义,其中上文提到的Eo数表征浮力与表面张力的相对大小,本节在维持初始表面张力不变的情况下,通过调节Eo数的值来得到不同的气泡运动状态,即研究浮力对气泡在微通道内上升的影响.在本文模拟中,分别考虑了Eo数为10,15,20,25,30,35和40七种情况.在所有情况中,θ=90◦,其他参数设置与5.1小节中相同.

图10为Eo=10时,气泡上升速度演化图和对应速度极值的运动瞬时图.从图10中可以看出,在演化初期,气泡上升速度在浮力的作用下逐渐增加,当气泡靠近障碍物时,受到障碍物的阻碍作用,其上升速度开始减小.随后气泡顶部挤过通道最窄部分其速度又逐渐增加,当所有气泡都穿过障碍物通道最窄部分时,由于通道截面的增加,其在表面张力作用下开始变形,对应的上升速度减小.随着气泡的形状趋近于圆形,表面张力的影响减弱,上升速度再次增加,气泡发生分裂现象,一部分残留在障碍物表面上,另一部分继续上升且形状逐渐恢复成下凹的球冠形,出现速度下降现象,此后气泡形状变化越来越小,气泡上升速度趋于稳定.该现象与上一小节现象一致.

图10 Eo=10时对应的气泡上升速度演化图和运动瞬时图Fig.10 .Time histories of the bubble velocity and the snapshots of the bubble at extreme positions under Eo=10.

图11 Eo=30时对应的气泡上升速度演化图和运动瞬时图Fig.11 .Time histories of the bubble velocity and the snapshots of the bubble at extreme positions under Eo=30.

图11为Eo=30时,气泡上升速度演化图和对应速度极值的运动瞬时图.对比图10和图11可以发现,Eo数的增大造成气泡上升速度变化趋势以及界面动力学行为出现显著的不同.一方面,当Eo=10时,气泡的上升速度相对较低,在运动过程中出现三个极大值、两个极小值的情况,而当Eo=30时,浮力相对于表面张力增加,气泡穿过障碍物通道的过程中与障碍物有明显的间隙,更容易通过障碍物通道,而且由于表面张力作用减弱,气泡通过障碍物通道后不再出现因为变形而导致速度减小的趋势,在运动过程中速度只出现两个极大值,一个极小值.Eo数的增大使得气泡在运动过程中整体上升速度增加,到达微通道终端所需时间减少,当Eo=30时,气泡会在T=13.89时刻到达通道终端,而对应Eo=10时,气泡会在T=16.52时刻到达通道终端.另一方面,Eo数不同时气泡的界面动力学行为也有较大不同.当Eo=10时,气泡紧贴障碍物壁面上升,在大部分气泡通过通道最窄处时,气泡底部形成两个“小圆孔”(T=7.01),此后气泡发生严重变形,逐渐形成一个类似“拱门”的形状.随后,在浮力作用下气泡发生分裂行为(T=9.59),一部分残留在障碍物表面上,另一部分则继续上升,完全脱离后的气泡在浮力作用下开始变形并逐渐恢复成下凹的球冠形.当Eo=30,气泡逐渐挤入障碍物通道时(T=3.56),受到的浮力更大,气泡下半部分变形更加剧烈,变形的弧度更明显,而且在气泡通过障碍物通道的过程中,上半部分基本不会与障碍物有接触,而下半部分在较大的浮力和一定的障碍物挤压力下,生成两个较长的“小触须”.随着时间演化,有一部分“小触须”穿过障碍物表面,另一部分残留在障碍物表面上,穿过的“小触须”在表面张力的作用下,重新形成球冠状随大气泡一起上升,初始两者并未融合,随着时间演化由“小触须”形成的那部分追上了上部分大气泡,两气泡合并后一起上升.

图12给出了不同Eo数下,气泡经障碍物通道到达微通道终端的剩余质量百分比Rq.从图12中可以看出,剩余质量百分比Rq随Eo数增大基本呈对数形式增加.当Eo=10时,剩余质量百分比Rq=73.26%,在此情况下,由于浮力相对于表面张力给予气泡的作用力并不明显,气泡在经过障碍物表面时,在浮力、表面张力和障碍物阻力共同作用下,发生破裂,破裂的气泡会残留在障碍物表面上.随着浮力逐渐增加,开始在整个力场占据主导地位,气泡能相对顺利地通过障碍物通道,从而破裂后残留在障碍物表面的气泡越来越少,其剩余质量百分比Rq增加.当浮力增加到一定值(Eo=30)时,气泡整体基本能完整地通过障碍物通道,气泡剩余质量百分比Rq基本保持不变.图13给出了不同Eo数对气泡终端速度vb的影响.从13图中可以看出,随着Eo数的增加,气泡终端速度vb的变化也基本呈现对数形式增加.当Eo数较小时,气泡到达微通道终端的终端速度vb随着Eo数增加得较快,当增加到一定值(Eo=30)时,增长速度逐渐放缓.

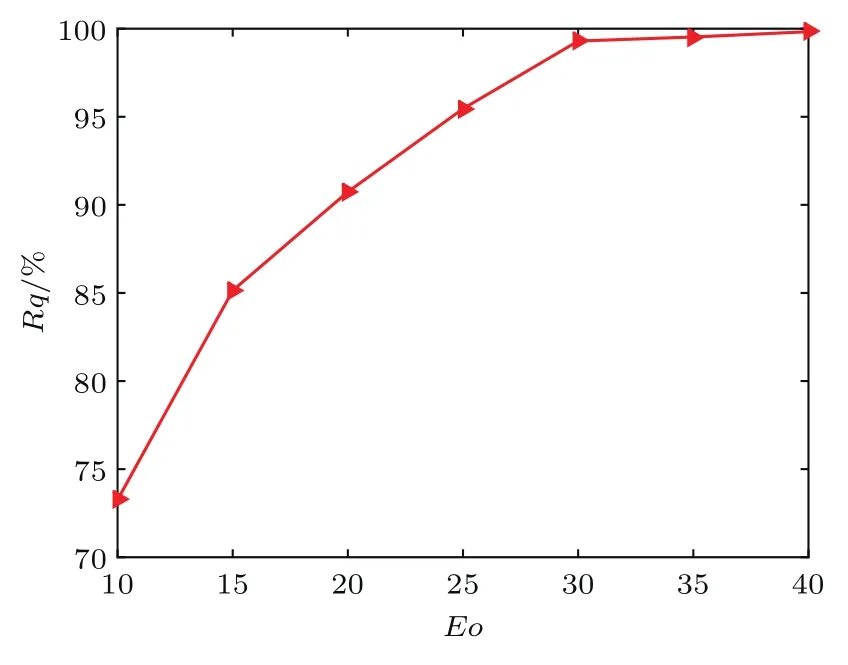
图12 不同Eo数下气泡剩余质量百分比Fig.12 .Percentage of the bubble residual mass obtained under dif f erent Eo numbers.

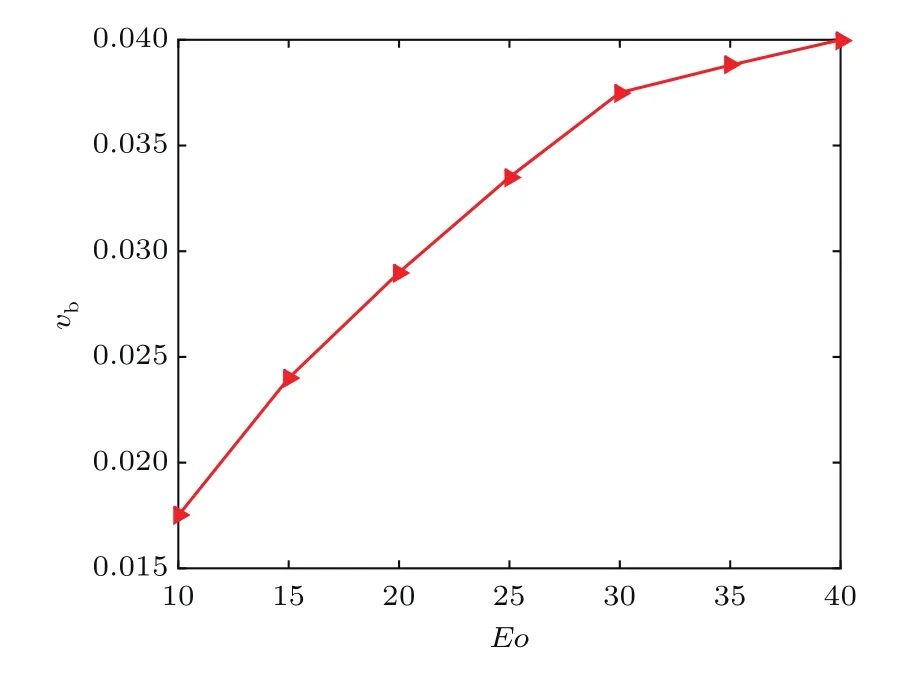
图13 不同Eo数下气泡的终端速度Fig.13 .Terminal velocities of the bubble under different Eo numbers.

5.3 障碍物尺寸的影响

障碍物作为微通道结构中重要的一环,其尺寸的改变会对气泡运动造成重要的影响,本节分析不同障碍物半径大小(R1=50,55,60,65,70)对气泡运动的影响.数值模拟中Eo=15,Mo=0.6802,θ=90◦,其余参数设置与5.1小节相同.

图14给出了障碍物半径为60和70时,气泡上升速度演化图和对应速度极值的运动瞬时图.从图14中可以看出,在气泡未到达障碍物通道前,气泡的上升速度变化趋势基本相同;在进入障碍物通道后,由于障碍物尺寸不同,气泡上升速度的值出现明显的不同.例如当R1=60时,气泡在通过障碍物通道过程中,受到障碍物的阻碍作用,上升速度由0.0403下降到0.0342;当R1=70时,气泡受到的阻碍更大,气泡上升速度由0.0278下降到0.0108.在气泡脱离障碍物表面并上升到微通道终端的过程中,不同障碍物半径对应的气泡上升速度变化趋势也不相同,比如当R1=60,气泡整体脱离障碍物时,气泡上升速度略微下降后出现振荡,之后因形状剧烈变化造成速度持续下降,直到形状稳定后(图14(a)T=10.38),速度逐渐趋于稳定;当R1=70时,由于气泡通过障碍物通道时受到的阻力较大,则气泡与障碍物脱离时上升速度较小,随后在浮力的作用下,速度略有上升,再因表面张力作用产生剧烈变形,变成下凹的球冠形,速度略微下降,再度趋于平稳(图14(b)中T=16.56时).障碍物半径的增加使得气泡通过障碍物通道更加困难,到达微通道终端的时间增加.当半径R1分别为60和70时,气泡到达微通道终端的时间分别为T=16.17和T=24.84.

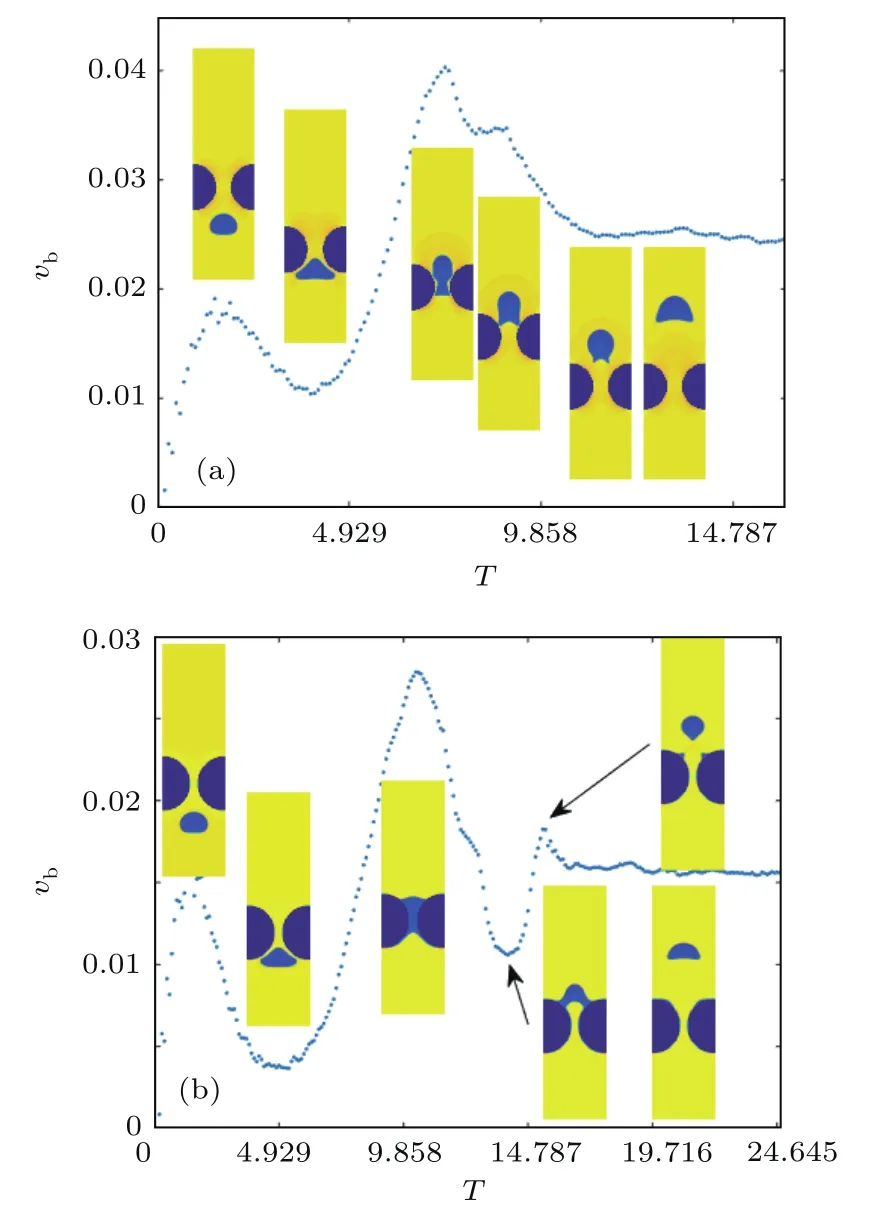
图14 障碍物半径不同时得到的气泡上升速度演化图和运动瞬时图 (a)R1=60;(b)R1=70Fig.14 .Time histories of the bubble velocity and the snapshots of the bubble under dif f erent values of radius:(a)R1=60;(b)R1=70.

相对应的,气泡形状的变化也会因障碍物尺寸不同而出现变化.在气泡挤入障碍物之间的通道后,半径为60的情况中,气泡在通过障碍物通道时,与障碍物表面之间有一定的间隙,气泡能较完整地通过障碍物通道,并以半圆形状继续上升;而半径为70的情况中,气泡完全紧贴障碍物表面上升,随后会出现“拱门”形状,且当气泡通过障碍物通道后,有部分气泡残留在障碍物表面,该情形下脱离后的气泡明显更小.

为进一步说明障碍物尺寸对气泡运动的影响,图15和图16展示了不同障碍物半径下,气泡剩余质量百分比Rq以及气泡终端速度vb的变化趋势.从图15中可以看出,气泡剩余质量百分比Rq的变化趋势表现为初期下降较慢而后期下降较快,这是因为障碍物半径较小时,大部分气泡能较顺利地通过障碍物通道,而随着障碍物半径增加到60以上时,气泡运动过程中受到的阻力增加,有相当一部分气泡破裂后残留在障碍物表面上,剩余质量百分比Rq随障碍物半径增加而迅速下降.从图16中可以看出,气泡终端速度随着障碍物半径的增加而近似呈线性减小,这是由于障碍物半径的增加,使得气泡通过障碍物通道更加困难,产生的变形更严重,从而终端速度降低.

图15 不同障碍物尺寸下气泡剩余质量百分比Fig.15 .Percentage of the bubble residual mass obtained for dif f erent sizes of the obstacle.

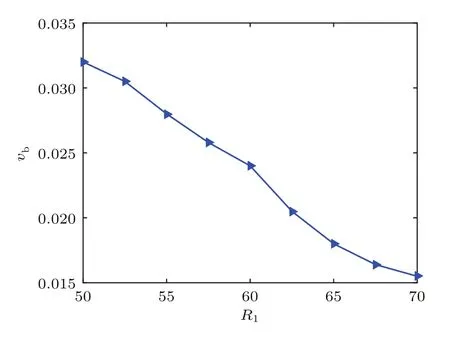
图16 不同障碍物尺寸下气泡终端速度Fig.16 .Terminal velocities of the bubble for dif f erent sizes of the obstacle.

5.4 气泡初始位置的影响

本小节研究气泡初始位置对气泡运动情况的影响.如图17所示,初始气泡圆心位置为(xd,yc),xd为距离左壁面的R2位置,yc则仍为微通道高度的五分之一,在数值模拟中考虑不同的Eo数情况:Eo=10,15,20,25,30,35和40.在所有情况中,θ=90◦,其他参数以及边界条件设置同5.1小节.

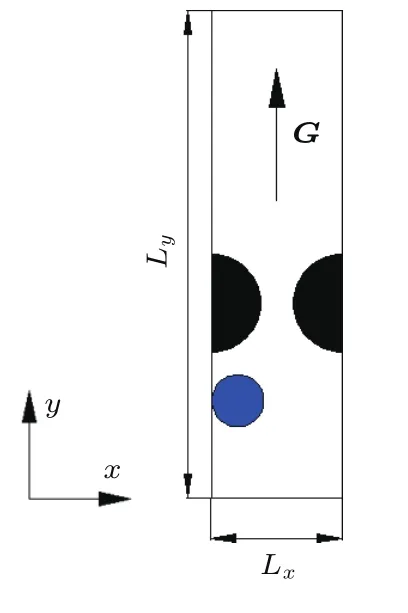
图17 模拟问题对比示意图Fig.17 .Comparison of simulation problem.

图18给出了气泡初始位置圆心为(xd,yc)情况下的气泡上升速度变化趋势以及对应速度极值的运动瞬时图(对应Eo=10).与图10相比,可以发现气泡初始放置在一侧时对应的上升速度变化趋势与气泡放置在管道中间时基本一致,同样出现三个极大值点和两个极小值点,但整体的上升速度均小于初始放置在通道中间的气泡上升速度,此情况与文献[20]给出的不同气泡初始位置的速度变化趋势类似.其中,气泡初始受浮力上升并即将挤入障碍物之间的通道时,初始气泡放置在一侧的情况中,气泡受到障碍物(尤其是左侧障碍物)的阻力更大,因此上升速度相对较低,气泡放置在一侧对应的上升速度值为0.0116,而气泡放置在管道中间对应的上升速度值为0.0165.相应地,在通过障碍物通道的过程中,初始气泡放置在一侧的情况下,对应气泡受到的阻力更大,上升速度由0.0209下降到0.0073,而气泡放置在管道中间的情况中,上升速度由0.0285下降到0.0182.两者到达微通道终端的终端速度也存在明显差异,气泡放置在一侧对应的终端速度为0.0128,气泡放置在中间对应的终端速度为0.0179.

从图18中还可以看出,演化初期由于气泡受力不平衡,在进入通道内最狭窄部分时,气泡已经发生了破裂现象,且在T=8.41时有少部分气泡会残留在微通道的左侧障碍物表面上.由于气泡进入障碍物通道时,左侧的障碍物与气泡的接触面积始终较大,在通过障碍物通道的过程中,左侧障碍物的阻力作用更明显,形成了整体偏左的“拱门”形状(此时T=11.72).随后在浮力和表面张力的共同作用下,气泡逐渐与障碍物脱离,有相当一部分气泡残留在障碍物表面上(此时T=15.19),而脱离的气泡继续上升,其形状慢慢恢复成为向左下方倾斜的球冠形,最终移动到微通道水平中心线位置并沿着水平中心线继续上升,但由于脱离气泡在挤出障碍物时,形状不对称,因此气泡到达微通道终端时仍会出现左右不对称现象.由此情况可以看到气泡与障碍物表面接触更普遍,障碍物的阻力作用更加明显,因此气泡变形更严重,上升过程更加困难,破裂并残留在障碍物表面的气泡更多.

图18 气泡初始放置在左侧时气泡上升速度演化图和运动瞬时图(Eo=10)Fig.18 .Time histories of the bubble velocity and the snapshots of the bubble at extreme positions when the bubble is initially set at the left side of the channel(Eo=10).

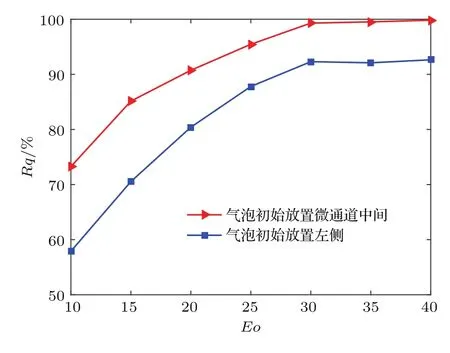
图19 不同的气泡初始位置下气泡剩余质量百分比Fig.19 .Percentage of the bubble residual mass for dif f erent initial positions of the bubble.

图19给出了两种气泡初始位置下,剩余质量百分比Rq随Eo数的变化趋势.从图19中可以发现,初始气泡位置不同时,其剩余质量百分比Rq整体趋势类似,Rq首先随Eo数增大而增加,然后再趋于稳定,但当气泡初始放置在通道一侧时,剩余质量百分比Rq相对较小.发生该现象是由于气泡初始放置在一侧时,上升过程中受力严重不平衡,因此变形现象更严重,表现为气泡上升过程中基本需完全接触左侧半圆形障碍,受到障碍物的阻力更明显,残留更多的气泡在障碍物表面,因此气泡的剩余质量百分比Rq相对较小.图20给出了两种不同气泡初始位置下,气泡终端速度vb随Eo数的变化趋势.从图20中可以清晰地看到,气泡初始位置不同时气泡终端速度vb的趋势基本一致,但气泡初始放置在一侧的情况中,气泡在上升过程中受到障碍物阻力更大,因此终端速度vb相对较小,与文献[20]中得到的结论一致.