免涂装耐候钢腐蚀后的疲劳试验研究*
2018-12-14梁健宇张玉玲
梁健宇 姚 谏, 张玉玲
(1.浙江大学建筑工程学院,杭州 310058;2.浙江树人大学城建学院,杭州 310015)
0 引言
腐蚀会造成钢结构截面削弱、刚度下降,可能导致其强度或稳定性不满足原设计要求,甚至会使结构破坏。因此防止或减缓钢材腐蚀并同时提高材料的力学性能具有重要的意义。使用耐大气腐蚀高性能钢材来代替传统钢材,是解决钢结构腐蚀问题的一条新途径[1]。
耐候钢在大气环境下具有优秀的耐腐蚀性,属于低合金高强度结构钢[2-3]。耐候钢是通过添加少量的铜、铬、镍等合金元素,使其在金属基体表面上形成致密且附着性很强的保护锈层[4-5]。外表的保护锈层能阻碍锈蚀进一步向表层内的基体扩散和发展,提高钢材的耐大气腐蚀性能[6]。
耐候钢在大气下的耐蚀性通常为普通钢的2~8倍[7-8],能在结构使用期内有效减少腐蚀带来的损失,降低维护成本甚至免维护,最终达到结构总成本的下降。
如今,耐候钢已应用于桥梁、铁路、汽车、建筑、输电塔等领域[8-10]。在桥梁、轨道上裸露使用,耐候钢处于带锈状态的同时,还需要承受循环荷载[6,11]。为了获得耐候钢腐蚀后的疲劳性能,得到其应力-疲劳寿命(S-N)曲线,本文对Q355NHD耐候钢及其焊接试件的腐蚀后疲劳性能进行试验研究。同时为了比较,还对涂装后的Q345qD普通钢进行了疲劳性能试验。
1 试件制作
Q355NHD耐候钢及其焊接试件(以下分别简称耐候钢试件和耐候钢焊接试件)分别为6个和5个,涂装后的 Q345qD普通钢试件(以下简称普通钢试件)6个,试件尺寸及构造如图1所示[12]。图1b示焊接试件中部对接焊采用CO2气体保护焊打底(焊丝 JQ.YJ501NiCrCu-1)、埋弧焊填充的方法焊接,埋弧焊采用PREMIER WELDTM Ni1K(直径4.8 mm)焊丝 +JF-B焊剂焊接,保留焊缝余高。普通钢试件的上下表面以及侧边都进行涂装处理(用喷砂处理方式净化试件表面,使表面质量达到 Sa2.5级,然后覆以80 μm环氧富锌底漆、150 μm环氧云铁中间漆和40 μm氟碳面漆),以模拟实际工程中涂装后的普通钢表面获得较好维护不产生锈点时的使用状态。
耐候钢试件及其焊接试件进行24 d乙酸盐雾循环腐蚀试验,其腐蚀时长相当于广州、江津大气自然腐蚀 21.55 年和 10.92 年[13]。
试件用Q355NHD耐候钢和Q345qD普通钢的非Fe主要化学元素组成以及力学性能如表1所示,表中fy、fu和Es分别为屈服强度、抗拉强度和弹性模量[13]。

表1 钢材非Fe主要化学元素组成及其力学性能指标Table 1 Main chemical elements except Fe and mechanical properties of the steels
2 疲劳试验
2.1 试验概况
试件疲劳试验在浙江树人大学结构试验大厅进行,加载采用1 000 kN液压伺服疲劳试验机进行加载,可提供最大轴力正负1 000 kN。疲劳试验机如图2所示。对试件采用应力控制加载。每个试件的荷载频率由荷载幅值以及试验机的运行状态决定。对不同的荷载幅值选用使疲劳试验机振动较小且荷载曲线符合正弦曲线形态的最大频率。为了保证试验安全,当试件疲劳裂纹贯穿厚度方向,并沿宽度方向扩展至试件宽度的约1/3时,认为其发生疲劳破坏,并将此时的荷载循环次数作为其疲劳寿命。
采用应力控制的单点法对试件进行疲劳试验,拉-拉循环加载,最小应力均为10 MPa;一个试件对应一个应力幅(最大应力与最小应力代数差),在对应应力水平下测得该试件的S-N曲线。从最高应力水平开始,逐级降低应力幅,记录在各级应力幅下试件的疲劳寿命,直到完成全部试验为止[14]。

图2 1 000 kN液压伺服疲劳试验机Fig.2 Hydraulic servo fatigue testing machine of 1 000 kN
2.2 疲劳试验结果及分析
2.2.1 试件断口形态
试件疲劳试验的典型断口如图3所示,图中1和2分别表示光滑区和粗糙区。腐蚀后耐候钢试件疲劳试验的典型断口如图3a所示:所有试件裂纹起始面均为在腐蚀试验中朝上的表面,即腐蚀较为严重的一面;裂纹出现后,先向宽度方向扩展,同时向厚度方向贯穿。因为腐蚀在表面产生腐蚀坑,造成了表面不平整,所以疲劳裂纹的形成基本发生在腐蚀坑处,腐蚀坑附近截面急剧变化产生的应力集中促成疲劳裂纹的产生与扩展。
腐蚀后耐候钢焊接试件疲劳试验的典型断口如图3b所示:断口均出现在焊缝处;明显的裂纹出现后,先沿着焊缝向宽度方向扩展,同时向厚度方向贯穿。

图3 试件疲劳试验断口示意Fig.3 Scrhematic diagram of fracture surface of specimens
普通钢试件在试件截面角部(如图3c左下角):疲劳裂纹出现后,先向厚度方向扩展;随着加载的进行,裂纹贯穿厚度方向后,裂纹的扩展方向发生改变,转变为往试件宽度方向发展,直至断裂,典型断口如图3c所示。腐蚀后的耐候钢试件试验段表面因腐蚀产生疲劳源,所以在该处产生了裂纹,最终导致与普通钢试件不同的断口方式。
此外,比较不同应力水平下的试件表面锈层发现,随着最大应力的增加,会加剧对表面锈层的破坏,导致其脱落。在实际工程中,耐候钢表面锈层脱落将会使腐蚀介质易于侵入基体,降低其耐大气腐蚀性。所以在实际使用耐候钢时,对承受循环荷载作用的高应力部位,宜采取涂装处理等防护措施,以免表面锈层脱落而降低耐腐蚀性。
2.2.2 试验数据分析
试验结果如表2所示,经回归分析,得到耐候钢试件、耐候钢焊接试件以及普通钢试件的S-N拟合曲线分别为:

式中:N为疲劳寿命;Δσ为应力幅。

表2 疲劳试验结果Table 2 The results of the fatigue test
式(1)在双对数坐标中的曲线形式如图4所示。显见,耐候钢的S-N曲线位于普通钢的下方,耐候钢焊接试件的S-N曲线位于3条曲线最下方,即在相同的循环周次下,涂装后普通钢的疲劳强度最高,耐候钢焊接试件的最低。

图4 疲劳试验结果与拟合曲线Fig.4 Fatigue test results and fitting curves
通过拟合曲线计算得到200万次寿命时,耐候钢试件、耐候钢焊接试件以及普通钢试件的应力幅分别为 217.95,178.54,343.39 MPa。
表3给出了按式(1)计算得到的不同疲劳寿命(循环周次)下3种试件的应力幅比值,表中Δσ耐、Δσ焊和Δσ普分别为耐候钢试件、焊接试件和普通钢试件的应力幅。可见,随着疲劳寿命增加,耐候钢试件相对普通钢试件、耐候钢焊接试件相对于耐候钢试件的疲劳强度降低百分比逐渐扩大。
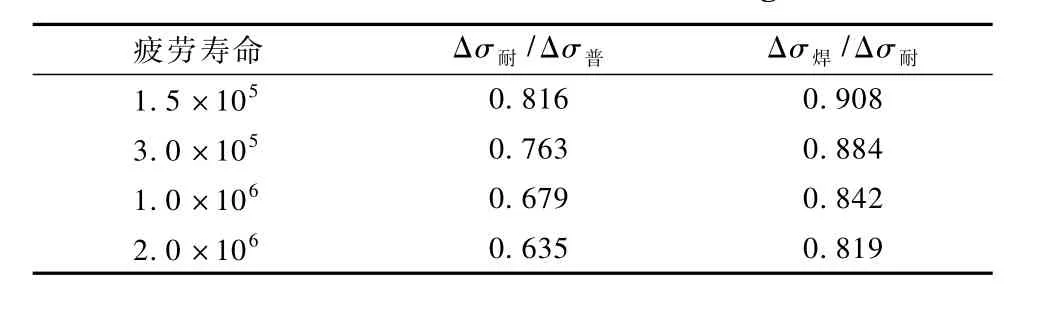
表3 应力幅比值Table 3 The radio of stress range
2.2.3 考虑存活率的S-N曲线
采用试验值拟合得到的S-N曲线,为50%存活率的曲线。实际工程中,通常会要求获得较高存活率P下的S-N曲线,即P-S-N曲线。所以确定P-S-N曲线对于结构材料的安全寿命预测研究具有重要意义[15-16]。文献[17]给出了基于单点法并采用极大似然估计对P-S-N曲线参数进行估计的方法。该计算方法基于三参数S-N曲线模型。下面简要介绍该方法的使用原理。常用的三参数S-N曲线模型为:

式中:m、C和 σ0为与材料性质等相关的参数。对式(2)等号两端取自然对数,并引入依赖应力幅的对数正态随机变量Z(Δσ),则式(2)变为:

Z(Δσ)的标准差为 s(Δσ)。从理论上可以证明[18]:当S-N曲线和P-S-N曲线在对数坐标系中为直线时,对数疲劳寿命的标准差将随着对数应力水平的降低而线性增大,通常假定与对数应力幅存在线性关系[17-18]。
根据lnN服从正态分布,获得其对数似然函数,然后根据极大似然原理解极大似然方程组即可获得ln C等相关参数。则存活率P下的疲劳寿命Np可根据下式获得:

式中:up为标准正态偏量;不同的存活率对应不同的值,见表 4。P-S-N 曲线计算过程如图 5 所示[16,19]。

表4 不同存活率下标准正态偏量取值表[21]Table 4 The standard positive deviation values at different survival rates
对试验数据(表2)进行三个参数S-N模型的拟合,可得耐候钢试件、耐候钢焊接试件以及普通钢试件的三参数S-N曲线如下:
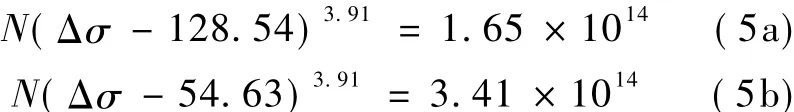

采用上述计算原理(图5),代入本文试验结果进行计算,计算过程以及参数的求解采用MATLAB计算软件实现。根据式(4)与表4的标准正态偏量,耐候钢试件、耐候钢焊接试件以及普通钢试件的三参数S-N曲线具有存活率P=90%的P-S-N曲线分别为:

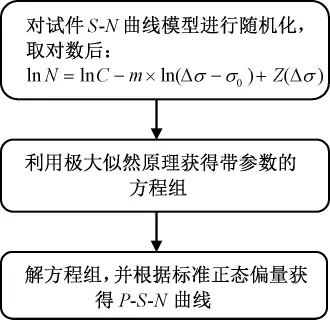
图5 P-S-N曲线计算流程[19]Fig.5 Calculation flow chart of P-S-N curve
图6 给出了式(6)—式(7)所示的P-S-N曲线。可以看出,P-S-N曲线与S-N曲线有相同的变化趋势,并且曲线形状较为相似;随着应力幅的增加,疲劳寿命不断减小;提高存活率,疲劳寿命明显下降,即随着存活率的不断增大,相应的P-S-N曲线相对于50%存活率的曲线不断下降,相同的疲劳寿命下,随着存活率的增加,对应的应力幅逐渐减小,结果趋于保守。通过计算结果发现,基于单点法试验所计算得到的P-S-N曲线,具有形式统一,整体规律较好的优点[22]。

图6 疲劳P-S-N曲线Fig.6 P-S-N curves
2.2.4 置信水平下 P-S-N曲线
为使估算出的疲劳寿命安全、可靠,需要考虑P-S-N曲线的置信水平 g,获得具有置信水平 γ、存活率P的疲劳寿命Npγ。文献[20]给出了利用 t分布[23]的特点,计算一定置信水平下的P-S-N曲线方法。利用该方法,计算得到本文耐候钢试件、耐候钢焊接试件以及普通钢试件在不同置信水平g、不同存活率P时的P-S-N曲线为(图7):


从图7可以看出,γ-P-S-N曲线与 P-S-N曲线虽然有相同的变化趋势、曲线相似,但是受置信水平影响较大。同一存活率下,当置信水平变为95%时,材料疲劳寿命有所下降,即P-S-N曲线会整体下降,结果偏向保守。当不考虑置信水平时,置信水平为0,γ-P-S-N曲线转化为P-S-N曲线。考虑置信水平的P-S-N曲线,因展现的是母体的真实值,故有一定概率落在与试验值有关的区间内。即置信区间提高了试验的可信程度,为使估算出的疲劳寿命安全、可靠,需要考虑P-S-N曲线的置信水平。

图7 疲劳γ-P-S-N曲线Fig.7 γ-P-S-N curves
通过计算结果可以发现,按照上述方法计算得到的γ-P-S-N曲线,变化趋势较为理想,变化分布合理,整体规律较好。
3 结束语
1)腐蚀后耐候钢的疲劳强度比涂装后普通钢的低,腐蚀后耐候钢焊接试件的疲劳强度最低。在疲劳寿命为2×106次时,耐候钢的疲劳强度为普通钢的63.5%,耐候钢焊接试件的疲劳强度为耐候钢的81.9%。腐蚀后试件表面产生的腐蚀坑以及焊接试件的焊缝处力学不均匀性是导致疲劳性能降低的主要原因。
2)基于极大似然估计法建立、分析三种试件的P-S-N以及γ-P-S-N曲线可知,提高存活率或置信水平时,在相同的疲劳寿命下,对应的应力幅减小,即考虑存活率或者置信水平的S-N曲线与50%存活率的基于试验结果拟合的S-N曲线相比更加安全,拟合得到的曲线更加可靠。
