多输入多输出—非正交多址接入系统融合用户调度的下行波束赋形设计
2018-12-14景小荣
刘 依,胡 哲,景小荣
(重庆邮电大学 通信与信息工程学院,重庆 400065)(*通信作者电子邮箱ly918124@163.com)
0 引言
随着移动互联网业务井喷式的发展,尤其是移动视频业务的拓展,对更大系统容量的无线接入技术的需求与日俱增。面对日益紧张的频谱资源和快速增长的移动业务,而传统的正交接入(Orthogonal Multiple Access, OMA)难以满足要求,亟需引入新型的多址接入技术[1]。在这种背景下,可支持多个用户同时传输的非正交多址(Non-Orthogonal Multiple Access, NOMA)技术引起了人们的注意,目前被认为是5G中非常具有前景的多址接入方案[2]。与传统的OMA不同,NOMA可实现多个用户同时同频传输信号[3]。在NOMA系统中,多个用户信号在功率域叠加起来进行传输,在接收端,采用串行干扰消除(Successive Interference Cancellation, SIC)技术依次恢复各用户的发送信号[4]; 同时,多输入多输出(Multiple Input Multiple Output,MIMO)可在不增加带宽和天线发送功率的条件下,成倍地提高频谱利用率, 因此,MIMO和NOMA技术的结合,即多输入多输出—非正交多址接入(Multiple Input Multiple Output-Non-Orthogonal Multiple Access, MIMO-NOMA)技术,将为5G中实现极高频谱效率提供强有力的保障。
然而,在MIMO-NOMA系统中,由于多个用户的发送信号在功率域叠加后在单个资源块上进行传输,将不可避免地造成严重的干扰。为了降低干扰的影响,现有研究通常按照某种准则对多用户进行分簇,在此基础上,发射端通过对波束赋型(BeamForming, BF)的优化设计来消除簇间干扰,同时,接收端采用SIC技术来消除簇内用户间的干扰。文献[6]中,采用信道相关性强的用户分到一簇的方法,对用户进行分簇,虽然该方法可在一定程度上取得较好性能,但对于信道相似度较大的簇内用户而言,当采用SIC技术进行信号恢复时,其性能有限; 文献[7-8]提出基于信道差异的用户调度算法,考虑将信道增益差异大的两个用户分为一簇, 但该分簇方法并未考虑用户信道相关性,使得簇间用户干扰较大,系统性能下降; 文献[9]采用随机BF设计消除簇间用户干扰,但该方法提升系统容量有限; 文献[10]提出一种基于用户信道相关条件分簇方法,通过迫零算法(Zero Forcing, ZF)设计BF矩阵, 但随着基站(Base Station, BS)端天线数增大,用户间相关性减弱,导致用户间干扰增大,系统性能显著下降。根据上述分析,用户调度方法应同时考虑用户信道差异和相关性,在此基础上,通过优化BF设计达到同时削弱簇内用户干扰和簇间用户干扰的目的,实现系统更优性能。
根据上述分析,本文融合用户调度,提出一种下行NOMA-BF方案。在该方案中,为了同时有效地处理簇内用户干扰和簇间用户干扰,在用户调度时,首先基于各用户信道的差异性,利用L1-范数正则化方法对所有用户分组情况进行初步稀疏处理;接着,从各用户信道相关性出发,根据上述初步稀疏化结果,将信道相关性大的两个用户分为一簇;最后,为了进一步消除簇间干扰,根据和速率最大化准则构建一目标函数,进而利用连续凸估计(Successive Convex Approximation, SCA)对其进行求解,以获得波束赋形矩阵。仿真实验结果表明, 该方案不仅有效地抑制了簇间干扰和簇内用户间干扰,同时,又在一定程度上保证了用户间的公平性。
1 系统模型
考虑一单小区MIMO-NOMA系统下行链路。假设小区中心位置配置一具有Nt根天线的基站(BS),为小区内M(M>2Nt)个单天线用户提供服务。在该系统中,将用户进行分簇,假设每个簇最多容纳2个用户,因此最多有2Nt个用户被同时调度,同时,处于同一簇的2个用户由BS端的同一根天线为其提供通信支持。根据上述假设,BS发送信号矢量x∈CNt×1可表示为:
(1)

令y∈C2Nt×1表示所有用户的接收信号,于是有:
y=H×W×x+n
(2)

2 问题提出
在该系统中每个用户接收到的信号不但包含了对应的期望信号,同时还包含来自簇内用户的干扰信号、其他簇用户的干扰信号以及加性高斯白噪声,于是,根据式(1)~(2),第i个簇的强用户接收到的信号可表示为式(3):
(3)
其中ni,1表示第i个簇中强用户的加性高斯白噪声。若假设在强用户端使用SIC可将簇内用户干扰完全消除。此时,强用户收到的信号可表示为式(4):
(4)
由于分配给弱用户的功率大于强用户,在弱用户端无法采用SIC消除簇内强用户干扰,所以,第i个簇的弱用户接收到的信号如式(5)所示:
(5)
其中ni,2表示第i个簇中弱用户的加性高斯白噪声。与该簇中两个用户对应的接收信干噪比(Signal to Interference plus Noise Ratio, SINR)可分别表示为:
(6)
根据式(6),第i个簇的强用户和弱用户速率分别为:
(7)
此时,根据式(7),基于系统和速率最大化准则,则可构建如下优化函数:
(8)
s.t.‖W‖≤1;SINRi,1≥γ0;SINRi,2≥γ0;i=1,2,…,Nt
其中:‖W‖≤1表示将BF矩阵归一化,γ0为保证用户通信质量的最低信噪比。
为了保证各簇内各用户尽可能地收到各自的期望信号,必须尽可能地削弱簇内用户干扰和簇间用户干扰, 为此本文提出一种融合用户调度的下行波束赋形方案。
3 融合用户调度的下行波束赋型设计
本章首先给出基于L1-范数正则化的自适应用户调度算法;进而,在此基础上,为了削弱簇内用户间干扰的影响,采用部分发射功率控制(Fractional Transmit Power Control, FTPC)[11]来实现簇内用户间的功率分配;最后,根据和速率最大化准则构建一目标函数,进而利用SCA对其进行求解,以获得波束赋形矩阵。
3.1 基于L1-范数正则化的自适应用户调度算法
在MIMO-NOMA系统中,由于簇间用户干扰和簇内用户干扰的存在,使得系统性能受到影响。于是,在设计用户调度方法时,综合考虑簇内用户干扰和簇间用户干扰问题,即在选择簇内用户时,首先考虑将用户间信道增益差异大的分为一组,这样则进一步通过功率分配后,有利于用户端采用SIC技术来消除簇内用户间干扰,从而提高信号检测性能;在此基础上,考虑所选用户之间的相关性,即将相关性越强的用户分为一簇以有利于BF设计,同时也有利于减小簇间干扰。但是,按照该方式进行用户分簇时,系统中部分用户有可能会无法同时满足这两个要求,导致其无法与其他用户成功配对成簇,于是,在本文方案中,对于这部分用户采用OMA接入方式。基于上述用户调度的思路,下面给出具体的步骤:
第一步 计算小区内每个用户的信道增益,按照降序排列后对每个用户进行编号,取信道增益最大前Nt个用户,组成集合S1,即S1={1,2,…,Nt};由剩下的用户组成集合S2,即S2={Nt+1,Nt+2,…,M},其中S1集合中的用户为必调度用户。
第二步 计算S1和S2集合里面所有用户的信道增益的差值,组成矩阵d,其中元素di, j-Nt=|hi-hj|,i∈S1,j∈S2,hi表示BS到第i个用户的信道系数矢量,令dmax为d中的最大值。
第三步 对S1和S2中所有可能的分簇情况进行初步稀疏化处理,使得稀疏后的Nt个用户分簇达到全局信道差异性最大化。由于L1-范数正则化可作为求解稀疏解的启发式算法[12],所以本文运用其来实现全局信道差异最大化处理,以实现对用户分簇的初步稀疏化处理。
(9)
s.t. 0≤um,i≤1;i=1,2,…,Nt;m=1,2,…,M-Nt
其中:d∈CNt×(M-Nt),u∈C(M-Nt)×Nt,λ=0.000 1。通过实验,λ取0.000 1时,可达到很好的稀疏度。
通过求解式(9),根据式(9)中u矩阵中的非零项,就可找出能达到全局信道差异最大的所有用户分组,即实现对S2中用户的初步稀疏筛选。

3.2 功率分配方法
在上述用户分簇的基础上,为了减弱簇内用户间的干扰影响,采用部分发射功率控制(Fractional Transmit Power Control, FTPC)[11]来进行簇内用户间的功率分配。于是,第i个簇中强用户和弱用户的功率可用式(10)表示:
(10)
其中:P表示BS端每根天线的最大发射功率;α表示衰减因子,取值范围0≤α≤1。由于和速率会随α的减小而增大,而边缘用户的速率会随α的增大而增大,所以折中考虑,本文将α的值取为0.5。
3.3 BF设计
完成用户分簇和功率分配后,已经实现了有效地削弱了簇间用户干扰的目的,本文将通过BF设计来减小簇间干扰的影响。
由于式(8)中目标函数为一非凸函数,目前很难找到其最优解[12],所以,本文先将非凸目标函数等价变换,变换成便于凸优化的形式,然后对变换后的非凸优化约束条件采用迭代的SCA[13]进行处理。下面分别进行说明。
3.3.1 等价形式转换

(11)
s.t. C1:‖W‖≤1
C2:γi,1-1≤SINRi,1
C3:γi,2-1≤SINRi,2
C4:γi,1>γ0+1
C5:γi,2>γ0+1
显然,目标函数已转化成了γ的几何平均数,即将原目标函数转化为递增的凹函数从而可进行等价求解[14],但优化约束条件C2和C3仍具有非凸性,所以本文采用SCA将非凸条件转化成凸条件。
3.3.2 非凸条件处理
针对等价变换后的形式(11),对其进行凸近似处理。
对于式(11)中的约束条件C2和C3,引入松弛变量:
将目标函数式(11)中的限制条件C2和C3分别变换为:
(12)
(13)
注意到式(12)和(13)依然具有非凸性,在此引入松弛变量F∈C2Nt×2,进一步采用一阶泰勒估计[15]将式(12)和(13)中的第3个表达式转化为:
(14)
(15)
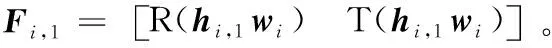
接着,根据多元函数的泰勒估计法,如式(16)所示:
f(x,y)≥f(xk,yk)+(x-xk)fx′(xk,yk)+
(y-yk)fy′(xk,yk)
(16)
将式(12)和(13)中的第4个表达式估计为式(17)和(18):
(17)
(18)
到此,目标函数式(19)被近似转化为凸优化问题,可运用cvx[16]有效获取全局最优。
基于上述公式推导,下面给出基于迭代SCA的BF算法的具体步骤:


(19)
s.t. ‖W‖≤1
γi,1≤bi,1+1
γi,2≤bi,2+1
γi,1>γ0+1
γi,2>γ0+1
i=1,2,…,Nt
4 仿真结果
本章通过数值仿真对文中提出的下行MIMO-NOMA系统中融合用户调度的NOMA-BF算法进行评估,仿真参数如表1[17-18]所示。在仿真中,BS处于小区中心,用户均匀分布在小区内。在仿真结果中,将本文所提出的融合用户调度的NOMA-BF算法(PUS-BF)与融合本文所提出的用户调度方案的迫零算法(PUS-ZF)、基于用户相关性进行用户分簇的ZF算法(C-ZF)[6]、基于用户相关性进行用户分簇的BF算法(C-BF)以及OMA进行对比。

表1 仿真参数
图1给出Nt=2,Pmax=46 dBm时,本文提出的PUS-BF算法与PUS-ZF、C-ZF、C-BF、OMA等算法的小区和速率随小区用户数变化的曲线。从图中可看出:所有NOMA算法的系统和速率均大于OMA,这说明NOMA相对于OMA来说在系统容量方面确实有大的提升; 同时,通过PUS-BF与C-BF, PUS-ZF和C-ZF算法的对比,本文提出的PUS-BF方案在小区和速率上表现出明显优势,这主要是因为在进行PUS-BF方案设计时,兼顾考虑了簇内用户干扰和簇间用户干扰。进一步,对比PUS-BF和PUS-ZF,说明用同样的用户调度策略,基于BF的方案要优于ZF算法。

图1 小区和速率随用户数变化的曲线
图2给出Nt=2,M=40时,本文提出的PUS-BF算法与PUS-ZF、C-ZF、C-BF、OMA等算法的小区和速率随BS端最大发射功率变化的曲线。从图2可以看出,随着发射功率的增大,这几种算法的小区和速率均随之上升,但本文提出的PUS-BF算法的性能明显要优于其他算法。同时注意到:在发射功率相对较小时,C-ZF和C-BF算法的小区和速率性能甚至比OMA还小,这是因为基于信道相关性的用户分簇方案将用户相关性较大的用户分为一簇,此时采用FTPC得到的同一个簇内两个用户的功率的差值也会相对变小,SIC有效性降低,导致簇内用户干扰抑制效果有限。而本文提出的PUS-BF算法在发射功率较小时,系统和速率依然要优于其他算法,这也进一步说明本文提出的用户调度方法在不同的发射功率下能同时有效削弱簇内用户干扰和簇间用户干扰。

图2 小区和速率随BS端最大发射功率变化的曲线
在Nt=2,M=40时,图3给出上述几种算法在各个方法下强用户和速率和弱用户和速率分别随BS端最大发射功率变化的曲线。从图3中可以看出,在不同的发射功率下,本文提出的PUS-BF方法下的强用户和速率与弱用户和速率都是最大的,且强用户和弱用户的和速率相差较小,进一步说明了在该用户调度算法下,不仅系统和速率得到了提升,用户之间的公平性也得到了足够保证。

图3 小区强用户和速率和弱用户和速率 随BS端最大发射功率变化的曲线
5 结语
MIMO-NOMA作为第5代移动通信系统的候选关键技术之一,将大幅度地提高系统的容量和频谱效率。为了发挥MIMO-NOMA技术的优势,文中通过研究下行MIMO-NOMA系统中融合用户调度的波束赋形问题,提出了一个新的用户调度策略,进而在该用户调度策略下,基于最大化和速率准则进行BF设计。仿真结果表明,本文提出的融合用户调度的BF算法不仅优于基于信道相关性用户分簇的ZF/BF算法和OMA,而且使用户间的公平性也得到保证。
