非对称占空比传感网中的广播能效优化算法
2018-12-14徐力杰
徐力杰
(1. 南京邮电大学 计算机学院、软件学院、网络空间安全学院, 南京 210023;2. 南京邮电大学 江苏省大数据安全与智能处理重点实验室, 南京 210023; 3. 南京大学 计算机软件新技术国家重点实验室, 南京 210023)(*通信作者电子邮箱ljxu@njupt.edu.cn)
0 引言
多跳广播作为无线传感器网络(Wireless Sensor Network, WSN)中的一项重要基本功能,近些年受到了越来越多研究者的关注。许多实际应用都要求sink节点将消息(例如配置命令、更新的代码等)以能量有效的方式分发到网络中的每一个传感器节点。为了极大地减少由于空闲侦听(idle listening)所带来的能量浪费,实际中的传感器节点通常都是以占空比(duty cycled)的方式进行工作[1],即每个节点周期性地在工作状态和睡眠状态之间交替切换, 这样的占空比工作方式在一定程度上导致广播能耗的低效性。如何为这样的网络设计能量高效的广播调度算法是一个重要且具有挑战性的问题。
很多现有工作[2-11]研究了占空比传感网中的广播能效优化问题。尽管如此,这些工作大多数都是将所有节点的广播总能量消耗作为刻画网络广播能效性能的准则。实际上,总能量消耗并不是传感网中刻画能量效率的最有效准则。很多典型的传感网应用都要求系统长期地部署在一些环境较为恶劣的场景中,在这样的场景下通常很难更换节点电池或给节点电池充电,这意味着节点的负载均衡性是能更有效刻画能量效率的准则,这是因为节点间不均衡的负载可能会让一部分承担了更多工作量的节点更快地耗尽了它们的能量,从而使得系统过早地失效。当前,大多数现有工作主要关注在占空比传感网中如何进行负载均衡的数据收集[12-15],非常少的工作考虑了数据分发(广播)的负载均衡问题。在实际中,一旦广播调度确定之后,它通常会被执行较长的一段时间,并且由于更新代价较高而通常不会频繁地动态更新广播调度。显然,没有经过优化设计的广播调度可能会导致节点间广播负载的高度不均衡性,因此,仔细地设计出一个面向占空比传感网的广播调度以实现节点间广播负载的均衡性是重要且具有挑战性的。
对于占空比传感网而言,广播延迟通常是一个首要考虑的性能准则。对于许多实际的广播应用,例如配置命令分发,每个节点都期望能够尽快地收到来自sink节点的广播消息及时更新自身的配置,以使得新的系统需求能够尽快地被满足。换句话说,很多实际广播应用都期望能够尽可能地减少从sink节点到每个传感器节点的端到端广播延迟。本文主要关注占空比传感网中最小端到端广播延迟约束下的广播能效优化问题。值得注意的是,这里的广播能效优化除了考虑了传统的广播总能量消耗优化之外,还重点考虑了广播的负载均衡优化,即节点的最大广播负载最小化。
在本文的前期工作[16]中,初步研究了占空比传感网中最小端到端广播延迟约束下的广播负载均衡问题,证明了该问题是NP难问题并且提出了一个有效的解决方法。尽管如此,文献[16]中作了一些严格的假设,例如假设了所有节点的占空比是对称的,即所有节点的占空比必须相同且每个工作调度周期里只能严格地包含一个活动时隙,并且还假设所有节点的传输功率都是相等且固定的。不同于前期工作[16],本文进一步放松了文献[16]中的假设,考虑了一个更加一般化的系统模型。具体地说,本文的工作可以适用于节点的占空比是非对称的情况,即允许各个节点可以灵活地定义不同的占空比,每个工作调度周期里允许包含任意多个活动时隙,并且假设了每个节点可以自适应地调节自身的传输功率,这样的假设更加具有实际意义。
1 系统模型与问题描述
本文假设时间被划分成一系列大小相等的时隙(time slot),并且每个时隙的长度设置能够保证一次数据包的传输。为了减少空闲侦听带来的能量浪费,整个网络假设采用占空比的工作方式,每个节点在部署之后可以根据一定的能量管理协议确定自身的工作调度。为了简便性且不失一般性,本文假设每个节点的工作调度是周期性的,且所有节点工作调度周期的长度T相同。具体地说,定义任意节点的每个工作调度周期由T个时隙组成,其中任意一个时隙t(t∈{0,1,…,T-1})要么是活动时隙要么是睡眠时隙。当一个节点处于活动时隙时,它将会开启自身的无线通信模块,并且可以进行数据的感知、信道的侦听以及数据的发送和接收;当一个节点处于睡眠时隙时,它将会关闭自身的无线通信模块,设置一个计时器(timer)以便在未来唤醒自己。因此,节点的占空比可以表示为一个工作调度周期内活动时隙的数量与一个工作调度周期内所有时隙数量的比值。这里,用每个工作调度周期内活动时隙的集合W(j)来表示任意节点j的工作调度,即:
(1)

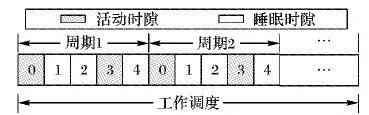
图1 周期性工作调度示例
不失一般性,本文允许各个节点定义不同的占空比,即对于任意节点i和j(i≠j),可以有|W(i) | ≠|W(j) |; 同时假设每个节点的传输功率共有m个离散的等级,即P1,P2, …,Pm,每个节点可以根据到接收节点的距离自适应地调节自身的传输功率等级。这里用无向图G(j)=(V,E(j)) (j=1,2,…,m)来表示当所有节点都采用传输功率等级Pj时形成的网络拓扑,其中V表示包括sink节点v0和所有感知节点{v1,v2,…,vN-1} 在内的N个拓扑节点的集合,E(j)表示所有通信链路的集合,任意两个节点之间存在一条通信链路当且仅当它们采用传输功率等级Pj时能够相互通信。
此外,本文也作了如下一些基本假设:1)网络中实现了时钟同步[17],由于只需要保证局部邻居节点间的时钟同步,因此实际开销并不大。2)为了便于描述且不失一般性,本文假设sink节点v0的每个工作调度周期内只包含一个活动时隙,即表示广播消息传输的起始时间。3)假设节点广播负载仅需考虑发送广播数据的能耗而无需考虑接收广播数据的能耗,这一假设在实际中是合理的,这是因为节点的空闲侦听模式通常和接收模式具有近乎相同的功率,且在本文的模型中每个节点仅仅在它调度的活动时隙内接收数据,这意味着所有节点接收数据的能耗可以近似地被忽略。4)本文主要面向链路质量可靠的网络,即假设网络中的链路质量是100%完全可靠的。
本文主要关注占空比传感网中最小端到端广播延迟约束下的广播能效优化问题,分别采用两种准则来刻画广播能效:一是节点的总能量消耗,二是节点的负载均衡性。这里假设网络中已经采用了某个现有的负载均衡的数据收集协议,该协议能够平衡由于节点间占空比的不同所带来的能耗差异,这意味着本文只需要考虑节点间广播负载的均衡性即可,而不必考虑节点间占空比的不同对节点能耗均衡的影响。
定义1 广播转发决策。对于网络中任意节点,它的广播转发决策表示为一组广播消息转发行为的集合,用f(vi) = {[转发时隙k,传输功率Pj] |k∈{0,1, …,T-1},j∈{1, 2, …,m}}来表示任意节点vi的广播转发决策,其中任意一个转发行为“[转发时隙k,传输功率Pj]”表示节点vi在下一个时隙k以传输功率等级Pj转发广播消息。特殊地,如果广播转发决策f(vi)为空集,则表示节点vi不是广播消息转发节点。
定义2 广播调度。 给定一个占空比传感网的拓扑图G(j)=(V,E(j))(j=1,2, …,m)以及V中所有节点的工作调度,V中所有节点的一组广播转发决策的集合M= {f(v) |v∈V}被称之为一个广播调度当且仅当M中的所有广播转发决策能够保证广播消息从源节点v0成功传输到每一个感知节点vi(i∈{1,2,…,N-1})。
本文的目标是解决如下两个问题:
问题1 最小延迟约束最小能量广播问题。给定一个占空比传感网的拓扑图G(j)=(V,E(j))(j=1,2,…,m)以及V中所有节点的工作调度,如何找到一个以sink节点v0为源节点的广播调度,在保证满足从v0到每个感知节点的端到端广播延迟最小的约束条件下使得所有节点的广播总能量消耗最小化。
问题2 最小延迟约束负载均衡广播问题。给定一个占空比传感网的拓扑图G(j)=(V,E(j))(j=1,2,…,m)以及V中所有节点的工作调度,如何找到一个以sink节点v0为源节点的广播调度,在保证满足从v0到每个感知节点的端到端广播延迟最小的约束条件下使得节点的最大广播负载最小化。
2 解决方法
2.1 问题建模
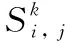
(2)
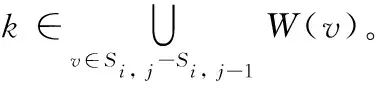
特殊地,定义Si,0=∅。此外,用c(Pj)表示当任意节点以传输功率等级Pj传输一个数据包时所消耗的能量。
为了便于问题的建模,本文首先将占空比网络的拓扑图转换成一个能清晰刻画广播时空特征的时空状态图Gs=(Vs,Es),其中Vs共包含两类顶点:拓扑顶点和状态顶点。每个拓扑顶点代表处于某个时间状态的V中的某个节点,用t′(v)表示任意拓扑顶点v的时间状态;每个状态顶点代表一个时空状态,用一个二元组〈时间状态t, 空间状态S〉来描述,它表示集合S中的所有节点在时隙t收到广播消息。
下面将介绍如何构造时空状态图Gs。
步骤1 对于V中的每一个节点v,分别构造|W(v)|个拓扑顶点与之对应。具体地说,对于每个t∈W(v),将构造一个对应的拓扑顶点v′,将其添加进Vs,并且定义它的时间状态t′(v′)=t。

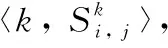
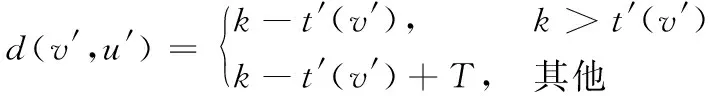
(3)
而对于Es中任意一条从状态顶点u′到拓扑顶点v′的有向边(u′,v′),定义它的延迟权重d(u′,v′)=0。
这里将用一个简单的示例来说明时空状态图的构造过程。图2给出了一个简单的网络拓扑图示例,其中工作调度周期长度T=10且任意节点vi旁边标注的集合表示它的工作调度W(vi)。图2(a)表示当所有节点采用传输功率等级P1时的网络拓扑G(1),图2(b)则表示网络拓扑G(2),G(3), …,G(m),其中m≥2。
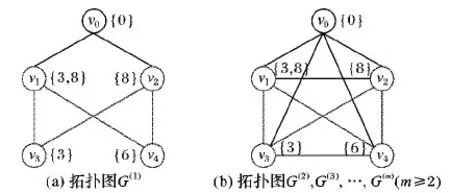
图2 网络拓扑图示例
根据定义可以得到:S0,1={v1,v2},S0,2={v1,v2,v3,v4},S1,1={v3,v4},S1,2={v2,v3,v4},S2,1={v3,v4},S2,2={v1,v3,v4},S3,1= {v1,v2},S3,2={v1,v2,v4},S4,1={v1,v2},S4,2={v1,v2,v3}。通过对图2所示的网络拓扑采用上述的方法,可以得到如图3所示的时空状态图,其中包含了拓扑顶点{v0′,v1′,v2′,v3′,v4′,v5′}和状态顶点{u1′,u2′,u3′,u4′,u5′,u6′,u7′}。在该示例中,只有节点v1的工作调度周期中包含了2个活动时隙,因此根据步骤1,分别构造2个拓扑顶点v1′和v2′来代表节点v1,并且定义t′(v1′) = 3,t′(v2′) = 8。节点v0、v2、v3、v4则可以分别用拓扑顶点v0′、v3′、v4′、v5′来代表,并且定义t′(v0′) = 0,t′(v3′) = 8,t′(v4′) = 3,t′(v5′) = 6。每条有向边的延迟权重由此可以通过步骤3计算得到。

图3 时空状态图的构造
不难发现,时空状态图很好地刻画了原始网络拓扑图中广播的时空特征。接下来,将在构造的时空状态图Gs中找到一棵以代表了sink节点v0的拓扑顶点v0′为根的最短延迟权重胖树(fat-tree)。本文采用一个类似于Dijkstra算法的方法可以很容易求得这样一棵最短延迟权重胖树。用ParentSet(Gs,v′)表示时空状态图Gs中任意非根顶点v′在最短延迟权重胖树上的父顶点集合,并且用ParentSet(G,v)表示原始网络拓扑图G(j)=(V,E(j)) (j=1,2,…,m)中任意非根节点v在最短延迟路径胖树上的父节点集合,用node(v)表示时空状态图Gs中的任意拓扑顶点v所代表的原始网络拓扑图中的节点。进一步地,通过如下的方式根据时空状态图中的最短延迟权重胖树得到原始网络拓扑图中的最短延迟路径胖树:对于任意非根节点vi∈V,用Su(vi)表示在时空状态图Gs里其空间状态覆盖了节点vi的所有状态顶点中最短延迟值D*(·)最小的状态顶点集合,不难得到vi的最优父节点集合
(4)
已知V中所有非根节点的最优父节点集合便可以构造出原始网络拓扑图中的一棵最短延迟路径胖树。根据所有非根节点的最优父节点集合,同样也可以得到原始网络拓扑图上任意节点v的最优子节点集合,用ChildrenSet(G,v)表示。换句话说,节点vi∈ParentSet(G,vj)当且仅当节点vj∈ChildrenSet(G,vi)。此外,对于任意节点vi∈V,用t′(vi)表示在时空状态图Gs里代表了节点vi的所有拓扑顶点中最短端到端延迟值最小的拓扑顶点的时间状态;对于任意节点vj∈ChildrenSet(G,vi),用P(vi,vj)表示节点vi能够与节点vj通信的最小传输功率等级。
为了更清晰地描述问题,为每个节点vi∈V定义了一个候选转发行为集合F(vi),并且通过如下的方式进行构造:初始地,定义F(vi)=∅。对于每个节点vj∈ChildrenSet(G,vi),将转发行为f=[t′(vj),P(vi,vj)]添加进F(vi),即F(vi) =F(vi)∪{f},这里用cost(vi,f)、coverage(vi,f)分别表示节点vi的转发行为f(即在t′(vj)时隙以P(vi,vj)功率等级转发)的能耗代价和接收节点覆盖范围,并且设置cost(vi,f) =c(P(vi,vj)),coverage(vi,f) = {v∈ChildrenSet(G,vi) |t′(v)=t′(vj) &&P(vi,v)≤P(vi,vj)},同时定义timeslot(vi,f) =t′(vj)为节点vi的转发行为f的时间状态。通过上述的方法,可以得到所有节点的候选转发行为集合。
具体地说,目标问题1可以等价于如下的最小代价转发行为子集覆盖问题(Minimum-Cost Forwarding Decision Subset Coverage Problem, MC-SCP)。
问题3 最小代价转发行为子集覆盖问题。已知所有节点的候选转发行为集合,如何为每个节点v∈V选择一个转发行为子集f(v)⊆F(v),以实现:

(5)
同时满足如下两个约束条件:
1)对于每个节点v∈V的转发行为子集f(v)中的任意两个不同的转发行为fi和fj,都有timeslot(v,fi)≠timeslot(v,fj);
类似地,目标问题2也可以等价于如下的代价均衡转发行为子集覆盖问题(Cost-Balanced Forwarding Decision Subset Coverage Problem, CB-SCP)。
问题4 代价均衡转发行为子集覆盖问题。已知所有节点的候选转发行为集合,如何为每个节点v∈V选择一个转发行为子集f(v)⊆F(v),以实现

(6)
同时满足如下两个约束条件:
1)对于每个节点v∈V的转发行为子集f(v)中的任意两个不同的转发行为fi和fj,都有timeslot(v,fi)≠timeslot(v,fj);
2.2 问题求解
本节将介绍如何求解问题3和问题4。
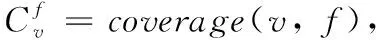
(7)
性质1 对于每个节点v∈V的转发行为子集f(v)中的任意两个不同的转发行为fi和fj,如果满足timeslot(v,fi) =timeslot(v,fj)且cost(v,fi) 根据2.1节中的定义,很容易发现性质1是一定成立的。在图3的例子中,很显然一定有coverage(v0, [3,P1])⊂coverage(v0, [3,P2])。由性质1可以得到如下的结论。 定理1 问题3等价于最小加权集合覆盖问题。 证毕。 由于已知最小加权集合覆盖问题是NP-hard问题,因此问题3也是NP-hard的。这里可以采用文献[18]中经典的贪婪算法(本文称之为最小代价转发行为子集覆盖算法(Minimum-Cost Forwarding Decision Subset Coverage Algorithm, MC-SCA))来解决问题3,该算法每一轮贪婪地选择“转发行为代价/新增覆盖节点数量”值最小的转发行为,即每一轮选择的转发行为能够以尽可能小的代价覆盖尽可能多的未被覆盖的节点。根据文献[18],可以容易证明该算法是求解问题3的一个H(dmax)-近似算法,其中调和级数H(dmax) = 1+1/2+…+1/dmax,且dmax表示在拓扑G(m)中的最大节点度。 由于问题4是文献[16]中目标问题的一般化问题,且文献[16]中的目标问题已经被证明是NP-hard问题,因此不难得出问题4一定是NP-hard问题。这里,本文提出如算法1所示的代价均衡转发行为子集覆盖算法(Cost-Balanced Forwarding Decision Subset Coverage Algorithm, CB-SCA)来解决问题4。在算法1中,用COST(v)表示任意节点v∈V的转发能耗负载,并且初始地赋值为0。对于每个节点v∈V中的每个候选转发行为f∈F(v),用z(v,f)表示当选择转发行为f时节点v的转发能耗负载与转发行为f带来的新增覆盖节点数量的比值。在每一轮迭代中,将以z(v,f)为贪婪准则选择z(v,f)值最小的转发行为,这是因为较小的z(v,f)意味着较小的节点v的转发能耗负载以及较多的新增覆盖节点数量。直觉上,每轮迭代选择一个使得对应节点所产生的转发能耗负载越小的转发行为能够使得最终所有节点产生的转发能耗负载最大值越小;同时,每轮迭代选择带来更多新增覆盖节点数量的转发行为在直觉上也能够减少迭代轮数,从而带来更好的能耗性能。 定理2 算法1一定能够得到问题4的可行解。 证明 由于算法1的每轮迭代都会带来一定新增的覆盖节点且迭代的终止条件是所有的节点{v1,v2,…,vN-1}被覆盖,因此很容易可知问题4的第2)个约束条件一定可以满足。这里主要证明算法1的求解结果一定能够满足问题4的第1)个约束条件。在算法1的第6~10行,对节点v中任意一个候选转发行为f判断是否在f(v)中存在一个时间状态为timeslot(v,f)的转发行为f′,如果存在,则有如下两种情况:1) 若cost(v,f) 证毕。 算法1 代价均衡转发行为子集覆盖算法。 输入 每个节点v∈V的候选转发行为集合F(v),以及每个转发行为f∈F(v)的能耗代价cost(v,f)和接收节点覆盖范围coverage(v,f)。 输出 每个节点v∈V的转发行为子集f(v)⊆F(v)。 1) 对于每个v∈V,初始定义f(v)=∅以及COST(v)=0; 2) S=∅; 3) WHILES≠{v1,v2,…,vN-1} 4) FOR 每个v∈V 5) FOR 每个f∈F(v) 6) IF 在f(v)中存在一个时间状态为timeslot(v,f)的转发行为f′ 7) z(v,f)=(COST(v)-cost(v,f′)+ cost(v,f))/|coverage(v,f)-S|; 8) ELSE 9) z(v,f)=(COST(v)+ cost(v,f))/|coverage(v,f)-S|; 10) END 11) END 12) END 13) 找到一个v*∈V以及一个f*∈F(v*),使得z(v*,f*)的值是所有z(v,f) (v∈V,f∈F(v))值中最小的; 14) IF 在f(v*)中存在一个时间状态为timeslot(v*,f*)的转发行为f″ 15) f(v*) =(f(v*)-{f″}) ∪ {f*}; 16) COST(v*) =COST(v*)-cost(v*,f″)+cost(v*,f*); 17) ELSE 18) f(v*) =f(v*) ∪ {f*}; 19) COST(v*) =COST(v*)+cost(v*,f*); 20) END 21) S=S∪coverage(v*,f*); 22) END 实验假设所有的传感器节点均匀地分布在一个100 m×100 m的监测区域,其中sink节点位于该监测区域的中心。假设每个节点的每个工作调度周期中最多包含两个活动时隙,具体地说,在实验中将每个节点的每个工作调度周期中的活动时隙数量设为1和2中的随机值(即每个节点的占空比为1/T或2/T),且每个节点独立且随机地确定自身的工作调度。通过这样的方式,可以简单且不失一般性地模拟节点占空比的非对称性。特殊地,对于sink节点v0,假设其每个工作调度周期仅包含一个活动时隙,且定义W(v0)={0}。这里除非特别指出,默认设置N=800,T=100。进一步地,假设每个节点有5个离散的传输功率等级{P1,P2,…,P5},其对应的最大传输距离分别为10 m、15 m、20 m、25 m和30 m,并且采用如式(8)的经典能量消耗模型来计算每个传输功率等级对应的节点传输能耗: ET(d)=l·ET-elec+l·εampd2 (8) 其中:d表示传输距离,ET-elec=50 nJ/bit,εamp=100 pJ/bit/m2,且广播数据包长度l设置为1 000 b。这里,所有的实验结果均是运行20次所得结果的平均值。 为了便于进行性能比较,本文提出了如下的两个基准方法: 1)随机父节点选择算法,该方法通过让原始网络拓扑图G上的任意非根节点v在ParentSet(G,v)中随机地选择一个节点作为它的父节点,从而生成一棵以v0为根的最短延迟路径广播树。 2)最小节点负载优先的贪心算法,该方法类似于算法1,唯一的不同在于对于贪心准则z(v,f)定义的不同,即将算法1的第7)行更改为z(v,f)=COST(v)-cost(v,f′)+cost(v,f),并且将第9)行更改为z(v,f)=COST(v)+cost(v,f)。 首先,比较了MC-SCA和随机父节点选择算法的广播总能耗性能。通过图4可以发现MC-SCA与典型的随机父节点选择算法相比其广播总能耗平均降低了24.23%,并且随着节点数量的增多以及节点工作调度周期长度的减小,MC-SCA的性能优势会变得更加显著,这是因为节点数量的增多和节点工作调度周期长度的减小会使得相邻节点工作调度的活动时隙发生重叠的概率变得更高,且重叠数量的期望变得更大,这显然对于本文使用的基于集合覆盖的方法能够带来更大的性能提升空间。 图4 MC-SCA和随机父节点选择算法广播总能量 消耗随着N和T变化时的性能比较 接着,验证了CB-SCA的性能。图5显示了CB-SCA与典型的随机父节点选择算法、最小节点负载优先的贪心算法以及MC-SCA相比其节点最大广播负载值分别平均降低了48.69%、10.64%和65.21%,因此CB-SCA具有更好的广播能量公平性。无论N和T如何变化,CB-SCA性能明显优于随机父节点选择算法和MC-SCA,这是因为后两种算法在设计过程中并没有考虑节点负载的均衡性。同时也发现CB-SCA在负载均衡性能上稍微优于最小节点负载优先的贪心算法,这两个算法在设计过程中都考虑了节点负载的均衡性,不同的是CB-SCA在贪心准则中除了考虑节点转发能耗负载外,还考虑了新增的覆盖节点数量,每轮迭代选择带来更多新增覆盖节点数量的转发行为能够一定程度上减少迭代轮数,从而可能对节点最大广播能量负载性能产生有利的影响。图5显示CB-SCA方法性能要优于最小节点负载优先的贪心算法,尽管如此,其性能优势并不是很明显。随着N的减小以及T的增加,相邻节点工作调度中活动时隙发生重叠的概率变得更小,且重叠的活动时隙数量期望变得更少,这意味着对于本文方法而言,新增覆盖节点数量在贪心准则中的作用变得越来越小,这将使得CB-SCA和最小节点负载优先的贪心算法的性能变得更加接近。 此外,还进一步验证了CB-SCA和最小节点负载优先的贪心算法在广播总能耗性能上的比较。图6显示CB-SCA始终能够获得比基准方法更好的广播总能耗性能,尤其是随着N的增加以及T的减小,其性能优势更加明显,这是因为相邻节点间更多重叠的活动时隙数量会使得新增覆盖节点数量在贪心准则中的作用变得更大,这在一定程度上能够减少迭代轮数,从而带来更好的广播总能耗性能。由此可见,无论是对于节点广播负载均衡性能还是对于广播总能耗性能而言,既考虑节点转发能耗负载又考虑新增覆盖节点数量的贪心准则始终都要优于仅考虑节点转发能耗负载的贪心准则。 图5 节点最大广播能量负载随着N和T变化时的性能比较 图6 两种面向负载均衡算法的广播总能耗 随着N和T变化时的性能比较 本文主要研究了占空比传感网中最小端到端延迟约束下的广播调度能效优化问题,并且分别从总能量消耗和负载均衡性两个方面来刻画广播调度的能效。首先, 研究了最小延迟约束最小能量广播问题,通过构造时空状态图将其建模成最小代价转发行为子集覆盖问题,同时证明了该问题等价于经典的最小加权集合覆盖问题; 随后, 研究了最小延迟约束负载均衡广播问题,通过将其建模成代价均衡转发行为子集覆盖问题,提出了一个高效的贪心算法解决该问题; 最终, 通过仿真实验验证了所提出算法的高效性。尽管如此,本文还存在一些不足之处,例如假设了链路质量是完全可靠的并且提出的算法是集中式的,如何在链路质量不可靠的网络中设计高效的分布式广播算法将是未来计划研究的方向。
3 仿真实验



4 结语
