面向K最近邻分类的遗传实例选择算法
2018-12-14黄宇扬董明刚
黄宇扬,董明刚,2,敬 超,2
(1.桂林理工大学 信息科学与工程学院,桂林 541004; 2.广西嵌入式技术与智能系统重点实验室(桂林理工大学),桂林541004)(*通信作者电子邮箱d2015mg@qq.com)
0 引言
K最近邻(K-Nearest Neighbors,KNN)分类算法是一种典型的非参数惰性学习方法[1],因其简单和有效使它被广泛用于分类问题[2-3]。它通过分析已知类的训练样本来预测新样本的类,因此训练集中的样本很大程度地影响了KNN的分类精度和分类效率。目前KNN分类方法存在的主要问题如下:1)训练集太大或数据的维数较高时,其计算的代价较高[4-5];2)训练集存在大量噪声样本时,会严重影响分类精度[6-8]。
实例选择算法可以有效缓解以上问题,通过对训练集样本的选择,在原训练集中寻找训练效果较好的代表样本集, 它通过缩减训练集来提高分类效率,同时通过删除噪声样本来提高分类精度, 因此实例选择受到关注。文献[5]通过“最邻近链”方法删除训练样本密集区中对分类决策影响不大的训练样本来减少训练集样本的数量; 文献[8]在处理二分类问题时,通过使用决策树对训练集进行预分类来确定噪声样本。
此外,进化算法[9]也是一种有效的实例选择方法[10-14]: 文献[10]将实例选择问题看作是一个遗传优化问题,在原有训练集的基础上生成不同的训练集组合,选择最优的训练集组合来代替原始的训练集; 文献[11]将遗传算法运用到实例选择中,并与非进化实例选择方法进行对比, 相较之下,它有着更高的分类精度; 文献[12]采用协同进化的方式,同时对样本和样本的特征进行选择,获得训练效果最佳的训练集及样本特征; 文献[13]同时优化样本权重和特征权重,根据最优的权重进行训练; 文献[14]将遗传算法与模糊粗糙集理论相结合,进行特征选择以提高KNN的分类精度。上述方法取得了不错的效果,但还存在以下问题:1)存在误删的风险,从而造成分类精度的降低;2)算法效率偏低。
本文主要研究如何为KNN选择最佳的实例集。研究内容及贡献如下:
1)提出基于决策树和遗传算法的二阶段筛选机制。先使用决策树确定噪声样本存在的范围,再使用遗传算法在该范围内精确删除噪声样本。该筛选机制能进一步提高分类精度,并缩小在训练集中进行实例选择的范围, 相较于对整个训练集进行实例选择的算法[7,12-13]有着较高的效率。
2)提出一种新的验证集选择策略。选择训练集中与测试集最邻近的样本组合成验证集,使遗传算法计算的适应度自适应不同的测试集,提高了实例选择的准确度。
3)引进一种新的遗传算法目标函数。将基于均方误差的分类精度惩罚函数MSE(Mean Square Error)作为目标函数能使遗传算法准确地找到最优的训练样本集,相比传统目标函数更为稳定和有效。
1 PRKNN算法
文献[8]提出了一种基于KNN的二分类实例选择方法(PRe-classification basedKNN, PRKNN), 在处理较大的数据集时,既提高了分类效率,又提高了分类精度。首先通过训练集构建决策树分类器,训练集中的每个样本都被划分到决策树的子叶节点中,经过决策树的分类后,训练集被分为几个不同的样本子集; 然后根据分类比率p(p是该样本子集正类样本的数量和总样本数量的比值)和阈值α(α<0.5)来判断这几个样本子集哪些是噪声样本大量存在的子集。如果该样本子集分类比率p≥α且≤1-α,则该样本子集确定为噪声样本大量存在的子集,这些样本子集将会被删除出训练集。ω=1表示将该样本子集留在训练集,ω=0表示将该样本子集删除,删减法则遵循式(1):
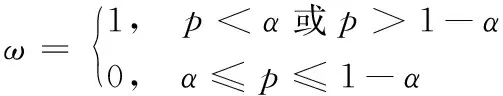
(1)
尽管PRKNN方法在提高KNN的分类效率和分类精度上取得了不错的效果; 但是在处理部分数据集时,由于删除掉的样本子集里包含有大量的非噪声样本,会严重地影响分类精度,甚至低于传统的KNN算法。为此本文采用其预分类的思想,提出了改进的遗传实例选择(Genetic Instance Selection,GIS)算法。 首先使用决策树初步确定噪声样本大量存在的范围;再使用遗传算法在该范围内精确定位并删除噪声样本。该方法相较于当前进化实例选择算法在分类精度和分类效率上均有一定程度的提升。
2 GIS算法
2.1 基于决策树与遗传算法的二阶段筛选机制
正如第1章所述,PRKNN算法将训练集进行预分类,把训练集分成几个样本子集;然后根据式(1)将一些样本子集从训练集中删除,但是这些样本子集中大概率包含非噪声样本,从而导致分类精度降低。本文算法不将这些样本子集完全删除,而将其中的样本加入噪声样本集Tnoise,其余样本作为非噪声样本保留在训练集中;随后使用遗传算法在Tnoise中精确删除噪声样本;最后,Tnoise剩余的样本与原来留下的样本组成训练集。为了使预分类思想能在多类问题中应用,本文算法将重新将p定义为主类占比,代表子集中最大同类样本数量和总样本数量的比值,同时α的范围变为α>0.5。若该样本子集p小于或等于α则该样本子集为噪声样本子集, 否则为非噪声样本子集,样本子集的确定遵循式(2):
(2)
如图1的例子,假设设定α的值为0.8。决策树将训练集分成A、B、C、D四个样本子集。子集A、D的p为0.88和1,均大于0.8,是非噪声样本子集,所以里面的样本将保留在训练集中; 子集B、C的p为0.56和0.5,为噪声样本子集,里面的样本将加入Tnoise,使用遗传算法进行进一步筛选,决定样本是否留在训练集中。
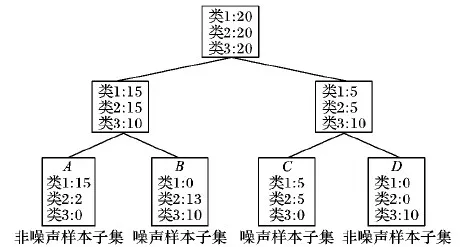
图1 噪声样本子集的确定
本文将对Tnoise的样本选择问题看作是一个遗传优化问题,在Tnoise的基础上生成不同的替代样本子集,对这些子集进行评价与对比,在进化一定的代数后选出最优的子集代替原来的Tnoise。
如图2所示,Tnoise的样本用N位的二进制向量b表示,N为所有Tnoise中包含的样本总量。每一位代表Tnoise里的每一个样本。如果b的第n位b[n]=1,则其代表的相应样本为非噪声样本,将保留在训练集中;反之将从训练集中删除。比特流b由给定目标函数的最小化来决定。如图3所示,本文将使用遗传算法获取最优的比特流b。
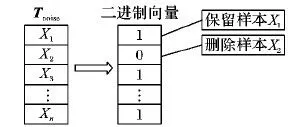
图2 噪声样本子集编码
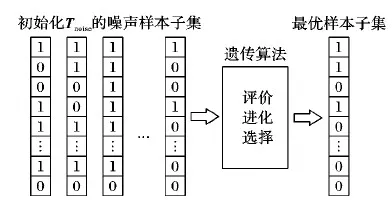
图3 遗传算法的应用
2.2 基于最近邻规则的验证集选择策略
传统的验证集是从训练集中随机选出与测试集等量的样本组合而成[7],用来辅助模型构建。该验证集选择方法存在以下问题:
1)当数据集较小时,从训练集中选出验证集会使训练集样本的数量进一步减少,对依赖训练集进行分类的KNN算法的分类精度产生很大的影响。
2)使用随机选取的验证集,由于它的随机性,构建出来的训练集会拟合于随机的验证集导致分类效果不太稳定。
针对以上不足,本文采用最近邻规则复制训练集中与测试集最邻近的样本来组成验证集。具体算法流程如下:
算法1 最近邻验证集选择算法。
输入 训练集为Tr,测试集为Te;
输出 验证集为Vs。
fori=1:测试集样本数量
forj=1:训练集样本的数量
ifTrj最邻近Tei
复制Trj到Vs
end if
end for
end for
该方法使验证集的特征更接近测试集。每一个测试集都会有一个与其对应的验证集,算法能通过这些验证集,自适应地构造出更有效的训练集; 可以避免因选出验证集后使训练集缩减导致的KNN分类精度损失; 同时,KNN使用该训练集进行分类,分类精度更高,分类效果更加稳定。
2.3 基于均方误差的分类精度惩罚函数
选择合适的遗传算法目标函数来计算适应度是获取最优训练集的关键。传统相关算法使用KNN的分类错误率作为目标函数并适当地增加惩罚(Counting Estimator with Penalizing Term, CEPT),如式(3)。验证集中的样本数量为N,若其中第n个样本Xn正确分类则h(Xn)=0,否则为1。
(3)
文献[7]在CEPT的基础上提出了更为有效和稳定的基于均方误差的分类精度惩罚函数MSE,如式(4):
(4)
其中:N表示验证集中样本的数量;C表示样本集的总类别;k表示k邻近值,kn[i]/k表示验证集中第n个样本被预测为第i类的概率;cn为该样本的真实类别。
2.4 GIS算法流程
算法的整体流程主要包含三大步骤:第一步,使用决策树确定噪声样本大量存在的范围即Tnoise;第二步,使用遗传算法从该范围中删除噪声样本;第三步,使用KNN进行分类。具体算法流程如下:
算法2 改进的基于KNN的实例选择算法。
输入 训练集为Tr,测试集为Te,最邻近值为k,噪声分部概率阈值为α;
输出 分类正确率为Ac。
1)
复制训练集中与测试集最邻近的样本组成验证集;
2)
在训练集上进行预分类,通过C4.5分类器将训练集划分为几个样本子集:T1、T2、T3,…,并计算样本子集的分类比率p1、p2、p3,…;
3)
fori=1:样本子集的数量
4)
Ti的主类占比小于等于α则将该子集的样本加入Tnoise,否则不做处理;
5)
根据Tnoise总的样本数量N,初始化包含有10个N位二进制向量个体的种群,其中1个二进制向量每一位都为1,其余9个随机产生;
6)
end for
7)
fori=1:30
8)
根据验证集计算种群中每一个个体对应的目标函数值,并保存全局最优值;
9)
使用轮盘赌法随机选择优秀的个体交叉产生10个个体;
10)
将二进制突变应用到整个种群中;
11)
end for
12)
利用经典的KNN算法基于全局最优个体对应的Tr对Te中的所有样本进行类别标号;
13)
输出标号后的数据集Te
其中,步骤1)验证集与测试集越相似,遗传算法得出的最优训练集越接近于测试集的最优训练集,最后对测试集进行KNN分类时分类的精度越高。步骤4)参数α的值设置太小,所确定的噪声区范围会偏大,使GIS算法在较小迭代次数和种群条件下得到的分类效果也偏低;参数α的值设置太大,会使噪声区太小或没有噪声区,导致GIS失去效果,相当于KNN。建议将α设置在0.1~0.3。步骤5)使初始化的初代种群有一个个体是每一位都为1的二进制向量。将其作为初代个体之一,可以保证在C4.5决策树分类器误将非噪声样本子集划分为噪声样本子集时,将保留原始的训练集作为最优训练集的备选个体之一。算法整体结构和流程如图4所示。

图4 GIS算法流程
3 实验结构
3.1 实验设置
为了验证算法的有效性,本文通过Keel编程实现算法,并在Win10系统下的Keel软件进行实验。对本文算法GIS、基于协同进化的实例特征选择算法(Instance and Feature Selection based on Cooperative Coevolution, IFS-CoCo)[12]、PRKNN算法[8]、经典KNN算法[1]这四个算法进行对比。实验数据来源于Keel平台标准的数据集库,大部分在UCI上有对应的数据集,数据集信息如表1所示。为了更好地验证GIS的可靠性和稳定性,数据集样本数量小于1 000的数据集使用3折交叉验证,大于1 000的使用5折交叉验证,实验10次取平均。四个算法k=7;GIS、PRKNNα=0.2;GIS、IFS-CoCo初始化10个个体,遗传迭代30次;四个算法其余参数按原算法默认值设置。
PRKNN只是二分类算法,本文通过重新定义p的方法将其扩展到多类(详见2.1节),不影响其处理二类问题的效果。
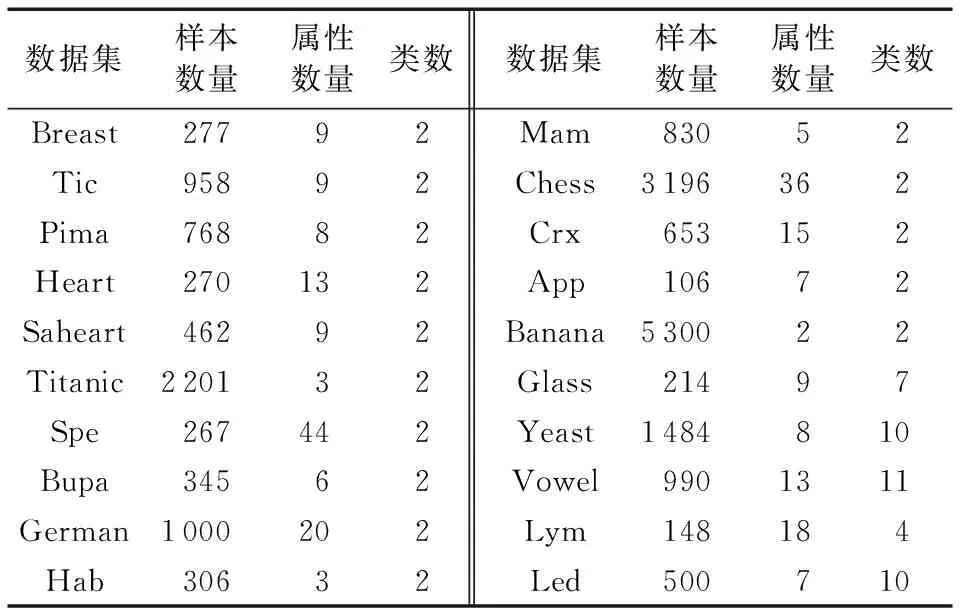
表1 数据集信息
3.2 评价标准
为了全面分析得到的实验结果,本文采用以下3种评价指标:
1)分类精度。分类精度是测试样本被正确分类的数量和测试样本总数量的比值,是衡量一个分类器分类效果的重要指标[15]。
2)AUC(Area Under Curve)。 AUC是接收者操作特征曲线ROC(Receiver Operating Characteristic)下方的面积[16],是判断二分类预测模型优劣的标准(ROC曲线的横坐标是伪阳率,纵坐标是真阳率)。为了计算AUC需要用到混淆矩阵来计算真阳率(Sensitivity)、伪阳率(Specificity)。
在混淆矩阵中,真阳性(TP)是正确分类的正类样本的数量;伪阳性(FP)是错误分类正类样本的数量;真阴性(TN)是正确分类的负类样本的数量;伪阴性(FN)是错误分类的负样本的数量。根据混淆矩阵,真阳率(Sensitivity)、伪阳率(Specificity)的计算公式如式(5)、式(6):
(5)
(6)
3)Kappa: Kappa系数从混淆矩阵中衍生出来的分类精度评价指标[17],代表被评价分类与完全随机分类相比产生错误减少的比例,它的计算公式如式(7):
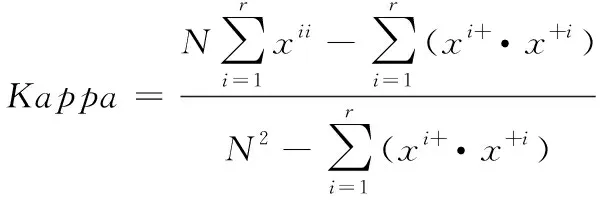
(7)
其中:r是它的行数,xii是i行i列(主对角线)上的值,xi+和x+i分别是第i行和第i列的和,N为测试集的样本数量。
AUC作为二类数据集的评价指标,Kappa系数作为多类数据集的评价指标,分类精度同时作为二类、多类数据集的评价指标。
4 实验结果分析
4.1 分类精度结果及分析
3.1节实验条件下,4个算法在数据集上的分类精度对比实验结果如表2(分类精度+标准差、每个数据集最优分类精度为粗体)所示。由实验数据可得:
1)GIS在测试数据集上的平均分类精度及最优分类精度占比(15/20)均高于其他三个对比算法。
2)GIS相较于PRKNN在分类精度上平均提高3.56%,提高范围为0.07%~26.9%。
3)GIS相较于IFS-CoCo在分类精度上平均提高1.52%,提高范围为0.03%~11.8%。
4)GIS相较于KNN在分类精度上平均提高1.66%,提高范围为0.2%~12.64%。
5)PRKNN在Titanic、Bupa数据集、IFS-CoCo在Tic-tac-toe(Tic)、Vowel数据集的实验中相对于其他算法有较大的精度损失(低于KNN 5%以上),导致平均精度较低,GIS比较稳定且平均精度高于其他对比算法。
6)同为进化实例选择算法,相较于IFS-CoCo,GIS能在较小的迭代评估次数下获得较优且稳定的分类精度。
7)在具体实例选择步骤分类结果的对比中,使用C4.5决策树进行实例选择时(PRKNN),平均分类精度最低(72.25%),当不进行实例选择时(KNN)平均分类精度为74.15%,当使用C4.5与遗传算法结合的二阶段筛选机制进行实例选择时(GIS)平均分类精度最高(75.81%),最优分类精度占比最高(15/20)。
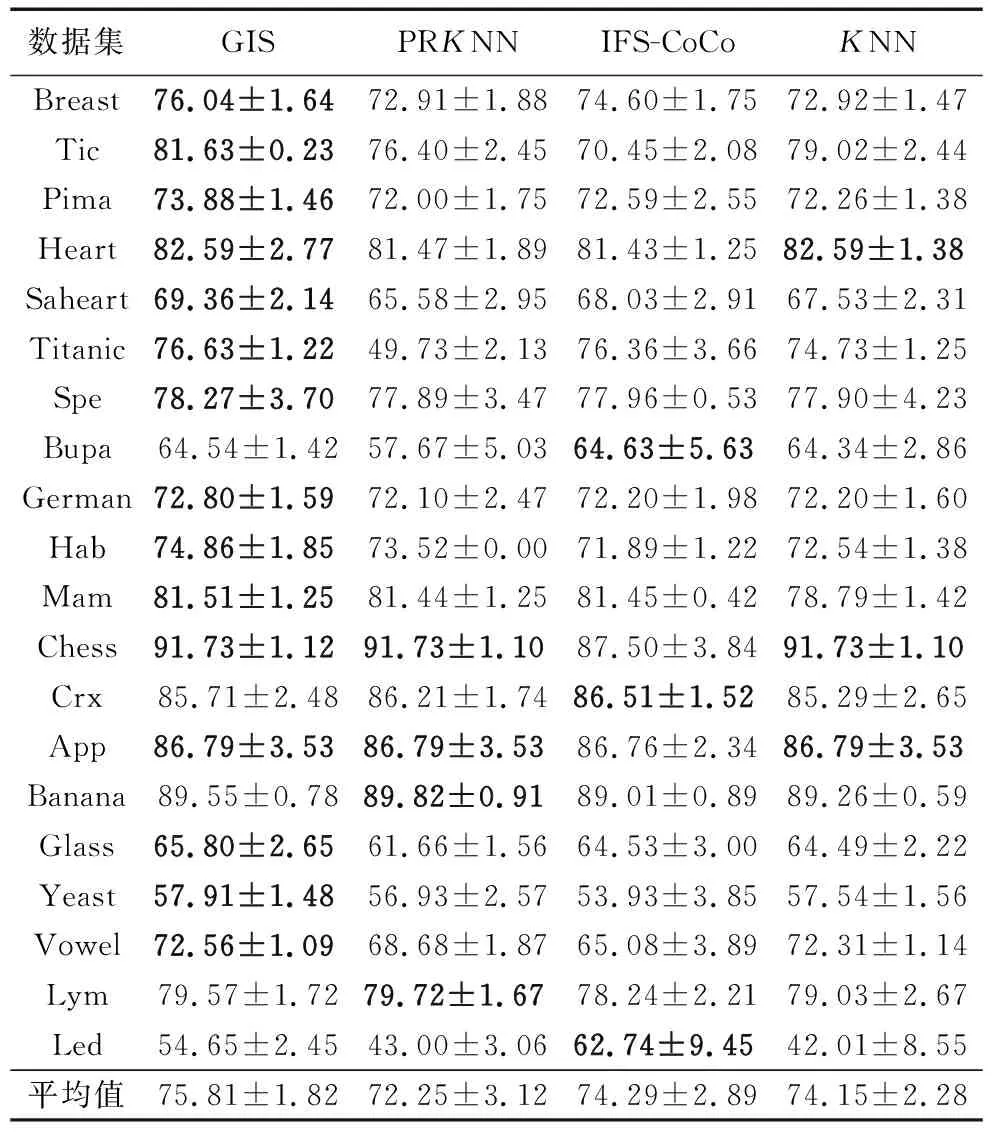
表2 4种算法分类精度实验结果 %
GIS与其他三个对比算法在分类精度上威尔克森秩和检验[18]结果如表3所示,不论与哪个算法相比,GIS的R+的值均远大于R-的值。P-value均远小于常规的显著水平(0.05),可以证明GIS在这组实验上的分类精度远优于其他对比算法。
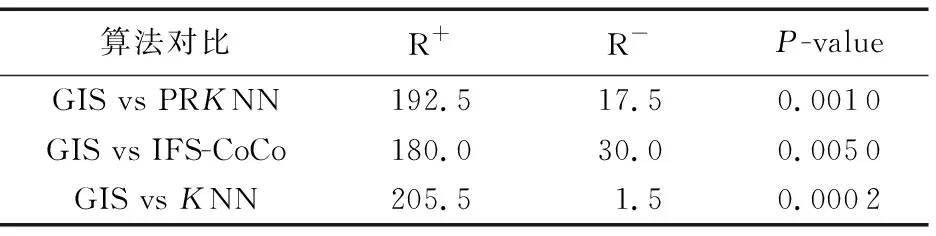
表3 分类精度威尔科克森符号秩和检验
综合以上分析,GIS算法分类精度优于其他三种对比算法。使用C4.5与遗传算法相结合的二阶段筛选机制,也优于不进行实例选择、使用C4.5进行实例选择。
4.2 AUC和Kappa结果及分析
在3.1节实验条件下,4个算法的AUC(二类数据集)、Kappa(多类数据集)对比实验结果(AUC或Kappa +标准差、每个数据集最优AUC或Kappa为粗体)如表4所示。
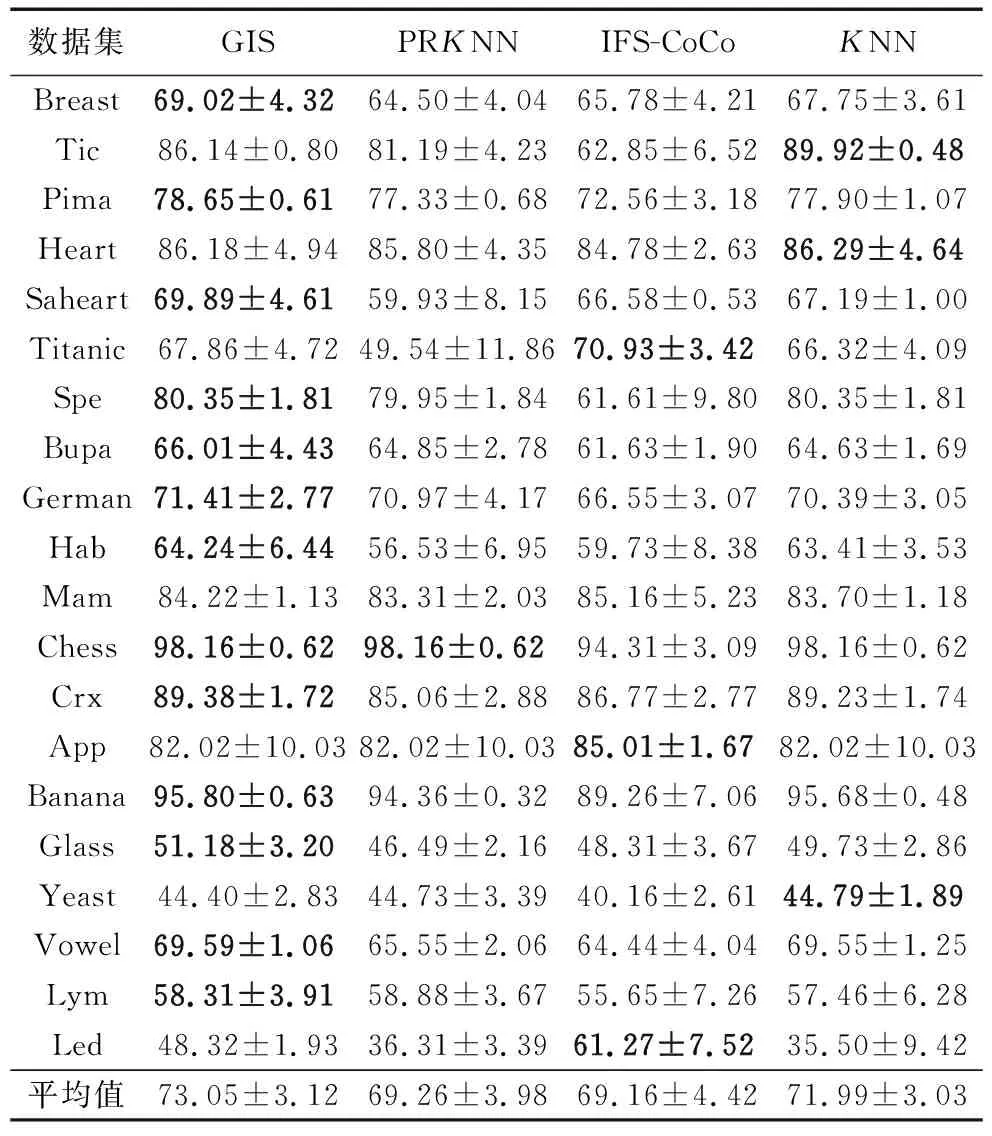
表4 4种算法AUC或Kappa实验结果 %
GIS算法与其他三个对比算法在AUC或Kappa上的威尔克森秩和检验结果如表5所示。
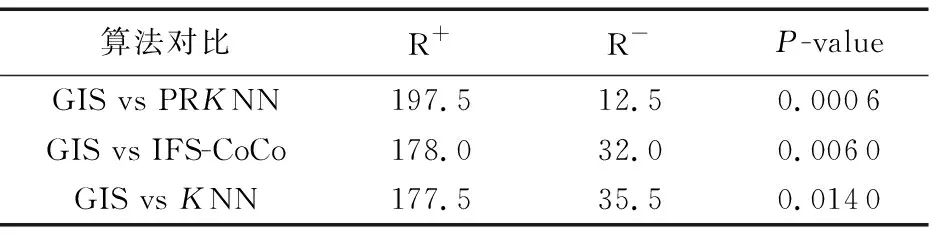
表5 AUC和Kappa威尔科克森符号秩和检验
由表5实验数据得:
1)GIS算法的AUC和Kappa均值及最优AUC和Kappa占比(13/20)均优于其他对比算法。
2)GIS相较于PRKNN在AUC和Kappa上平均提高3.79%,提高范围为0.25%~18.32%。
3)GIS相较于IF-CoCo在AUC和Kappa上平均提高3.89%,提高范围1.27%~23.29%。
4)GIS相较于KNN在AUC和Kappa上平均提高1.06%,提高范围0.04%~12.82%。
5)PRKNN在数据集Tic、Saheart、Titanic、Haberman有较大的AUC损失(低于KNN5%以上)。IFS-CoCo在数据集Tic、Pima、Spectfhear、Banana、Vowel有较大的AUC和Kappa损失。
由表4实验数据得:每一组对比实验,P-value均小于常规的显著水平,可以证明GIS在AUC和Kappa上优于其他对比算法。
如果不能精确地删除训练集中的噪声样本,会对依靠训练集进行分类的分类算法产生严重的影响,即使能提高分类精度,也可能造成AUC和Kappa的损失。GIS有效降低了误删率,提高了AUC和Kappa和稳定性。
5 讨论
5.1 遗传算法策略有效性讨论
为了更好地验证最近邻验证集选择(Nearest Verification set Selection, NVS)策略和遗传算法适应度计算策略MSE的有效性,本文将采用不同的验证集选择策略包括NVS、随机验证集选择(Random Verification set Selection, RVS)策略与不同的适应度计算策略包括CEPT、MSE两两组合进行配对实验。
在3.1节实验条件下,对遗传算法策略验证的实验结果如表6(分类精度+标准差、最优分类精度为粗体)和图5所示,由实验数据可知:
1)NVS+MSE的遗传组合策略在测试数据集的平均分类精度及最优分类精度占比(16/20)均优于其他三种对比策略。
2)NVS的验证集选择策略相对于RVS策略对分类精度平均提高1.11%(CEPT)、1.96%(MSE),有着较大的提升。
3)MSE+NVS相对于CEPT+NVS的策略组合对平均分类精度有1%的提升。
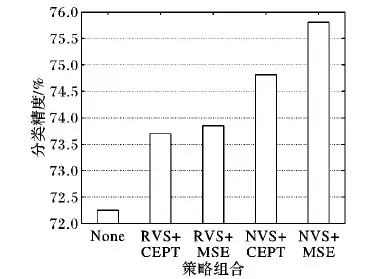
图5 遗传算法策略验证
NVS+MSE策略与其他策略在分类精度上的威尔克森秩和检验结果如表7所示,其中MSE vs CEPT测试是在屏蔽掉NVS的对比测试即RVS+MSE vs RVS+CEPT,同样的NVS vs RVS屏蔽了MSE。由实验数据可知:
1)在MSE vs CEPT实验中,R+与R-的差值为51,P-value也偏大,说明在此次实验中MSE相对于CEPT对分类精度提升不明显。
2)在NVS vs RVS实验中,R+与R-的差值为117,且P-value小于常规显著水平,说明NVS相对于RVS对分类精度有较显著的提升。
3)NVS+MSE策略对比其他的策略,P-value均远小于常规显著水平。
综合以上分析,GIS在使用NVS+MSE的遗传算法策略进行实例选择时。能提高实例选择的精确度,准确删除噪声样本,提高GIS的分类精度。在该组合策略中NSV起主要作用,与MSE结合能得到最好的效果。
5.2 算法时间复杂度讨论
面向KNN的进化训练集选择算法主要的时间消耗来源于每次进化迭代过程中对适应度的计算。IFS-CoCo采用协同进化的方式同时进行实例选择(Instance Selection, IS)、特征选择(Feature Selection, FS)及实例和特征选择(Instance and Feature Selection, IFS)。每次迭代需要计算三个适应度(IS、FS、IFS分别的适应度)。 它不引进验证集,直接使用原始的训练集进行训练,所以每次计算适应度的时间复杂度为
3O(N·S),N为训练集中样本的数量,S为从训练集中选择样本的数量。GIS引进验证集,只进行IS,时间复杂度为O(M·S),M为验证集样本的数量(M≤N)。IFS-CoCo是基于整个训练集进行全局寻优,GIS使用C4.5进行噪声范围定位后再进行准确的局部寻优,所以GIS在遗传算法的时间复杂度上小于IFS-CoCo。综合以上分析GIS在时间复杂度上小于IFS-CoCo。
虽然GIS的时间复杂度高于PRKNN,但由第4章的实验结果可知GIS在分类精度、AUC和Kappa及分类效果的稳定性上远优于PRKNN。
6 结语
本文提出了一种新的面向KNN的遗传实例选择算法GIS来提高KNN的分类精度。先通过C4.5决策树确定噪声样本大量存在的范围;再使用遗传算法在这个范围内精确地删除噪声样本,进一步提升了分类精度。相对于当前进化实例选择算法效率更高,效果更好。本文还提出一种新的遗传实例选择策略NSV+MSE,遗传算法使用该策略进行实例选择时,能针对不同的测试集选择出更适合它们的训练集,从而有效提升遗传算法进行实例选择的准确度。
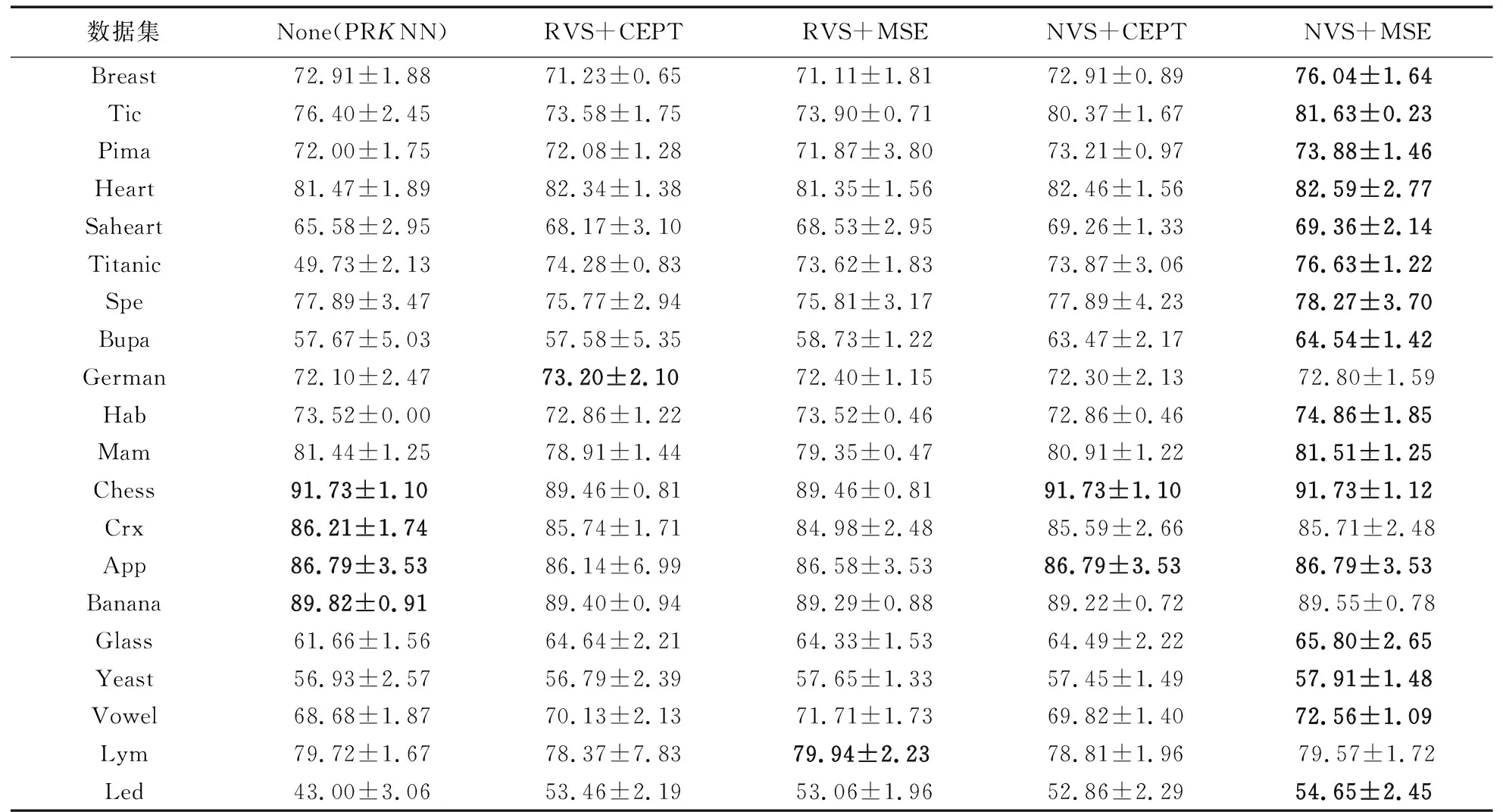
表6 5种遗传算法策略的分类精度实验结果 %
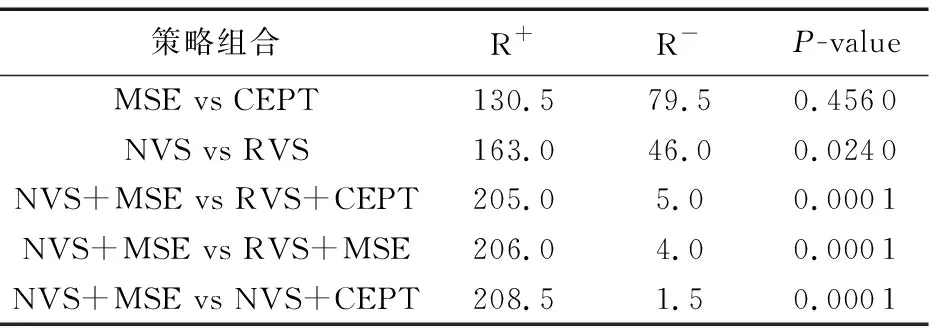
表7 遗传算法策略威尔克森秩和检验
经验证GIS 综合性能优于传统KNN、PRKNN、IFS-CoCo等算法,NSV+MSE也优于传统的遗传实例选择策略。
GIS未来的研究方向如下:1)GIS算法的两个关键参数k和α均需要手动设置,可以将它们改成自适应的形式以提高算法的智能性;2)在对噪声区进行实例选择时,可以不局限于样本的选择,可以扩展到特征选择。样本选择与特征选择相结合或许能进一步提升分类精度;3)使用新的遗传算法代替原始的遗传算法进实例选择。
