基于DDF2的RTS平滑方法在机载分布式POS中的应用
2018-12-14邹思远李建利曲春宇
邹思远,李建利,曲春宇
(北京航空航天大学,北京100191)
0 引言
机载对地观测系统是以飞机为载体,利用遥感载荷设备获取地球表面高精度、多层次空间信息的一种综合性技术,其被广泛应用于资源监测、城市规划、防洪减灾以及农业估产等领域[1]。目前,机载多任务遥感载荷高精度对地观测已经成为空基对地观测的重要发展方向,如集成高分辨率测绘相机、成像光谱仪、大视场红外扫描仪、合成孔径雷达(Synthetic Aperture Radar,SAR)于同一载机的多任务载荷,机载分布式阵列天线SAR,以及柔性多基线干涉SAR等[2]。多任务、多载荷对地观测系统要实现高精度成像,需要首先获取各遥感载荷安装点处的高精度运动参数。
位置姿态测量系统(Position and Orientation System,POS)是目前机载对地观测系统获取遥感载荷安装点运动参数的主要手段[3]。POS通常由惯性测量单元(Inertial Measurement Unit,IMU)、全球定位系统(Global Position System,GPS)接收机、导航计算机(POS Computer System,PCS)和后处理软件组成[4]。POS能够为载机及其遥感设备提供高精度的位置、速度、姿态等信息。但是,对于多任务遥感载荷对地观测系统而言,传统的POS已经无法满足不同载荷安置点的高精度运动参数的测量需求。因此,必须建立高精度机载分布式POS,从而为机载对地观测系统中遥感载荷各安置点提供高精度运动参数。
机载分布式POS系统一般由1个高精度主POS和多个分布在机体(包括机翼)上的低精度子IMU组成。主POS通过传递对准将高精度的位置、速度、姿态等运动参数传递给子IMU,从而获得各子节点的高精度运动参数信息。传递对准技术是分布式POS实现高精度测量的关键技术。
然而,分布式POS仍面临诸多技术问题。柔性基线效应引起的大失准角下的系统强非线性问题,严重影响了传递对准后处理估计与校正的精度。传统的、基于Kalman滤波(KF)的RTS线性平滑方法(KFRTS)已经无法满足分布式POS的测量需求。为解决柔性基线效应导致的精度下降问题,更加适用的非线性传递对准估计方法亟待研究。扩展Kalman滤波器(EKF)通过一阶Taylor展开将非线性系统线性化,被广泛用于解决非线性问题。然而,通过一阶Taylor展开的线性化会产生截断误差,在强非线性系统中估计精度低[5]。无迹Kalman滤波器(UKF)直接使用系统的非线性模型,不需要计算Jacob矩阵,而无迹变换具有局部和全局采样问题,且通常需进行大量的计算[6]。粒子滤波[7]、预测滤波[8]以及鲁棒观测器[9]等各种非线性滤波方法被应用于非线性模型中,但往往也带来了巨大的计算量。二阶插值微分滤波器(DDF2)可以应用于任何非线性函数,通过使用Stirling插值公式,用于非线性模型的多项式展开[10]。它可以避免产生误差积累的、非对称不稳定的估计误差协方差矩阵。然而,这些滤波器多适用于实时估计,不能充分利用所有量测信息,无法满足事后测量对高精度的需求。
固定区间平滑是最常用的事后估计算法,包括RTS平滑和双滤波器平滑(Two-Filter Smoother,TFS)2种。RTS平滑相比TFS平滑算法,避免了后向滤波,计算效率较高。本文针对机载分布式POS的非线性后处理问题,提出了一种基于DDF2的RTS平滑估计方法。前向滤波采用非线性滤波器DDF2,逆序平滑采用RTS平滑估计,得到了高精度的平滑估计结果。将此方法应用于柔性基线分布式POS的事后传递对准,提高了测量精度。
1 分布式POS非线性模型的建立
柔性基线效应会导致分布式POS出现大失准角,在传递对准过程中,子IMU系统模型为非线性,传统线性模型不再适用。为解决上述问题,建立非线性分布式POS传递对准模型如下。
1.1 状态方程
基于大失准角的姿态微分方程、速度误差微分方程、位置微分方程及惯性器件误差微分方程如下:
其中,ϕ是失准角,是姿态误差矩阵,是导航坐标系相对惯性坐标系的角速度在导航坐标系下的投影,是的误差角速度,是姿态矩阵,εs是陀螺漂移,Vn是载体相对导航坐标系的速度,δVn是载体的速度误差,VE、VN、VU分别为载体沿东向、北向、天向的速度分量,fb是加速度计测量值比力,是地球坐标系相对惯性坐标系的角速度,是地球坐标系相对惯性坐标系的误差角速度,是导航坐标系相对地球坐标系的角速度,是导航坐标系相对地球坐标系的误差角速度,Δs是加速度计偏置。
考虑大失准角带来的非线性误差,姿态矩阵表示如下:
其中,ϕE、ϕN、ϕU是失准角沿东向、北向及天向的分量。
根据式(1)~式(4),可得系统状态方程:
其中,xk是15维状态向量,f(·)是动态模型函数,wk是高斯随机过程噪声。
1.2 量测方程
采用“位置速度”匹配方式进行传递对准。分布式POS在传递对准过程中由杆臂引起的主POS和第I个子IMU之间的位置差矢量为:
分布式POS在传递对准中由杆臂引起的主POS和第I个子IMU之间的速度差矢量可表示为:
根据式(7),通过杆臂补偿后,子IMU的位置可表示为:
其中,Pm代表主 POS的位置,有:。
根据式(9),由主POS通过杆臂补偿到的子IMU的速度为:
其中,Vm表示主 POS的速度,有
通过以上推导,可得量测方程为:
其中,δLI、 δλI和δhI表示第I个子 IMU传递对准时的位置量测量,LI′、λI′和hI′表示第I个子IMU通过捷联解算得到的纬度、经度和高度,、和表示第I个子IMU传递对准时的速度量测量,、和表示第I个子IMU通过捷联解算得到的东向、北向和天向速度,表示第I个子IMU的量测噪声,其协方差用RI表示。
2 基于DDF2的RTS平滑估计方法
2.1 基于DDF2的前向滤波
插值滤波是利用Stirling内插公式对非线性模型进行多项式展开,将非线性函数进行插值多项式展开,取其一阶或二阶项作为函数的近似,然后采用Kalman进行递推的一种非线性滤波方法。该方法无需进行函数的偏导数运算,可应用于任意非线性函数,其估计精度较高。DDF2的算法如下:
(1)初始化
(2)一步预测
(3)量测修正
先验协方差的Cholesky因子可通过下列矩阵的Householder变换获得:
其中,Swk-1,j和表示矩阵Swk-1和的第j列元素,fi(·) 表示f(·) 的第i行。Swk-1是系统噪声矩阵的Cholesky因子,有:。Syk可通过以下复合矩阵的Householder变换得到:
(4)估计误差方差阵
(5)逆序模型参数计算
为提供逆序平滑所需的参数,可以使用加权统计线性回归(WSLR)对状态模型线性化,线性模型如下:
其中,Φk+1,k和bx,k是加权统计线性参数;ξx,k是线性化误差,为零均值白噪声,且协方差矩阵为Pξx,k;Γk是系统噪声驱动阵。上述参数计算如下:
2.2 RTS平滑
逆序执行RTS平滑的算法如下,其中,k=N-1,N-2,…2,1,0,且有初值为:
平滑增益矩阵为:
平滑状态估计为:
平滑估计误差协方差为:
最终的平滑估计结果用于反馈校正捷联解算后的误差,并获得子IMU的高精度运动信息。
3 实验验证
为了验证所提出的估计方法在分布式POS传递对准后处理的估计性能,本文进行了车载实验。
(1)实验条件
车载实验设备包括:工程实验车、主IMU、子IMU和GPS设备。设备以环形激光(RLG)IMU作为主系统,由3个随机漂移为0.01(°)/h的激光陀螺仪和3个零偏为50μg的加速度计组成。光纤(FOG)IMU作为子IMU,由3个随机漂移为0.02(°)/h的光纤陀螺和3个零偏为50μg的加速度计组成。车辆沿着计划路线驾驶,以完成成像任务。其中,平直段是最适合成像的区域。主IMU与GPS间的刚性杆臂为:=[-0.62m 0.175m 0.085m];主IMU与子IMU间的刚性杆臂为:=[0.175m-0.180m 0.002m]。主子IMU间的安装角误差为:△ϕ=[-0.3051°-0.0877°-0.1015°]。 为模拟机载分布式POS传递对准,在主子刚性杆臂上附加模拟杆臂的柔性变形。
(2)实验处理及结果
将现有的基于KF的RTS(KFRTS)和提出的基于DDF2的RTS平滑方法(DDRTS)分别用于获取车载POS传递对准,以获得子IMU的运动信息。以经刚性杠杆臂补偿后的主POS的运动信息为基准,表1给出了实验中使用的平滑器参数,图1为成像区域子IMU的航向角误差图,图2为成像区域子IMU的俯仰角误差图,图3为成像区域子IMU的横滚角误差图,表2给出了对成像区域子IMU的姿态误差的RMSE统计结果。
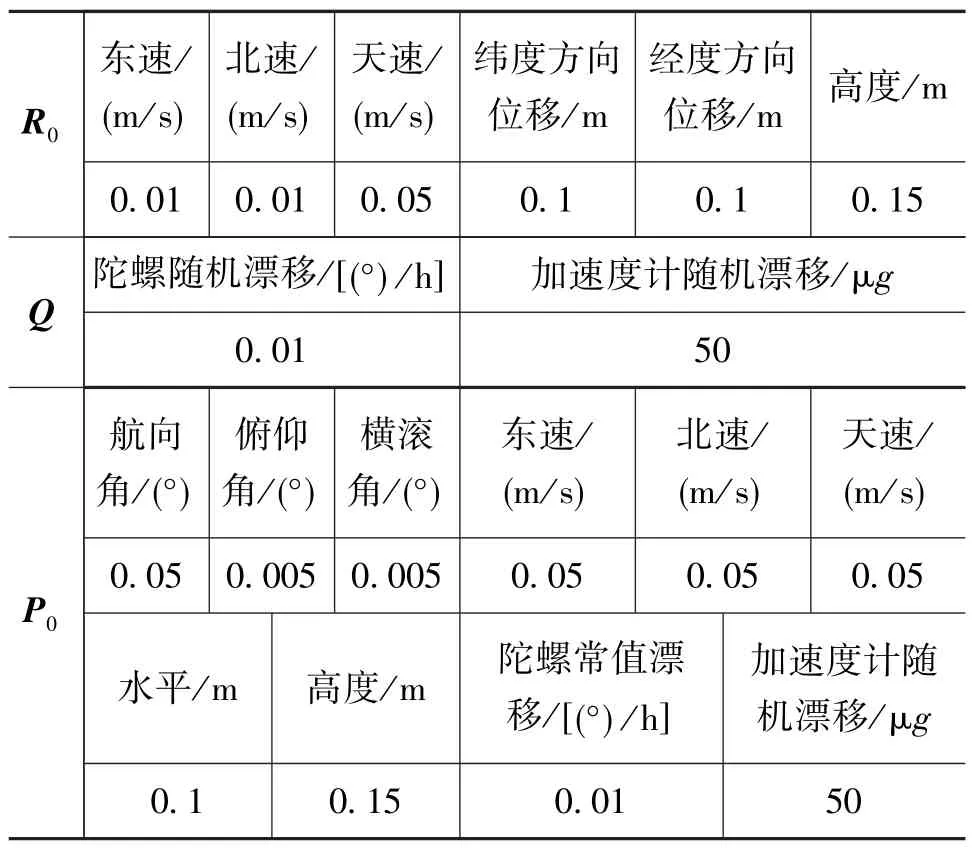
表1 滤波参数Table 1 Parameters of filter in experiment
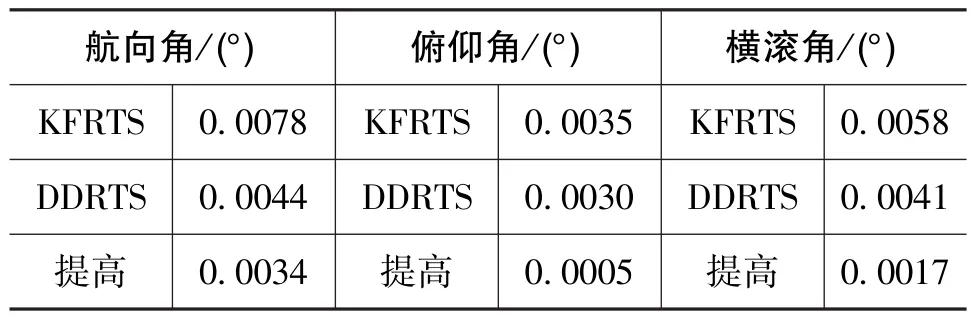
表2 子IMU传递对准姿态误差结果(RMSE)Table 2 Attitude precision of sub-IMU (RMSE)
实验结果表明,DDRTS可以提高运动参数的精度。以RMSE作为精度评估标准并与传统方法比较,通过DDRTS处理数据相比传统方法,使分布式POS子IMU航向精度提高了0.0034°(43.59%)。由此可以看出,DDRTS后处理估计方法能够显著提高分布式POS传递对准估计精度,可以成功应用于分布式POS的事后传递对准。
4 结论
本文提出的基于非线性二阶插值滤波的RTS平滑方法,相比传统线性RTS平滑方法具有更好的估计性能,将其应用于分布式POS传递对准后处理,可有效提高子IMU的测量精度,使航向精度提高43.59%,提升了分布式POS的测量性能。
