一种优化高度通道的行人导航算法
2018-12-14周绍磊李松林戴洪德全闻捷
周绍磊,李松林,戴洪德,全闻捷
(海军航空大学,山东烟台264001)
零速修正(Zero-Velocity Updating,ZUPT)[1-3]是目前惯性行人导航最常用的抑制和消除导航误差的方法。Elwell[4]首次提出了人在行走过程中存在零速区间的特性。随后,E.Foxlin[5]全面、系统地介绍了将惯性导航系统安装在足部的行人导航方法,并利用零速修正对导航参数误差进行校正,取得了较为理想的实验结果。在此基础上,国内外学者David[6]、Park[7]、Maan[8]、Carlos[9]、Terra[10]、高哲[11]、赵小明[12]、田晓春[13]等对惯性行人导航的零速修正算法做了进一步的研究,这些研究的共同特点是在同一零速区间内同时进行水平误差校正和高度误差校正,在纯惯性导航条件下,这种零速校正方法会使高度误差很快发散。
本文在研究零速区间的区间长度对导航精度的影响时发现,在同一零速区间内同时进行水平误差校正和高度误差校正不能使导航精度达到综合最高,因为使得高度误差达到最小的零速区间与使得水平误差达到最小的零速区间不一样。研究发现相对水平误差校正,高度误差在更严格的零速区间进行校正,可达到更高的导航精度。因此,本文提出一种将水平误差和高度误差分开校正的方法,即在不同的零速区间划分下分别进行水平误差校正和高度误差校正。经大量实验验证,本文提出的零速校正算法能在纯惯性导航系统下对高度误差进行有效抑制,并达到很高的高度估计精度,为行人导航系统提供了可靠参考。
1 零速检测
本文利用一种基于伪标准差和N-P准则算法进行零速检测,该检测算法仅需要进行一次比较就能够准确判断零速区间,该算法的检测步骤如下。
步骤1:假设(G yrox(k),Gyroy(k),Gyroz(k))为k时刻三轴陀螺仪的输出。按照滑动窗口的方法选取一个采样窗口k=[i-s,i+s],其中s为半窗口采样数,并求得这个采样窗口内所有陀螺仪输出的2s+1个模值:
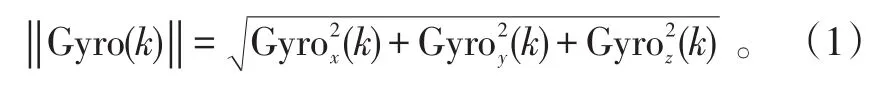
步骤2:将步骤1求得的2s+1个模值加上2s个0扩充为一个含有4s+1个元素的数列:
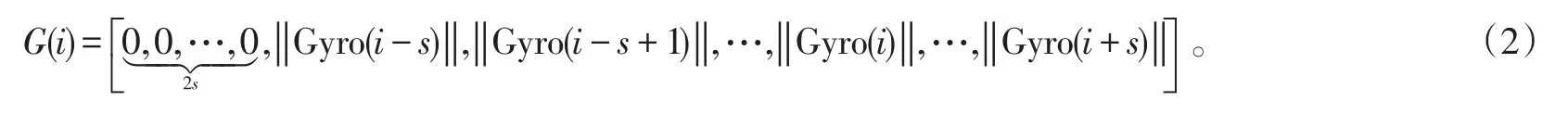
步骤3:对步骤2得到的扩充数列求取标准差,并称为陀螺仪模值的伪标准差:

步骤4:将步骤3求得的伪标准差值与阈值作比较,若标准差值小于阈值则判定采样点为零速区间。反之,则判定采样点为非零速区间。
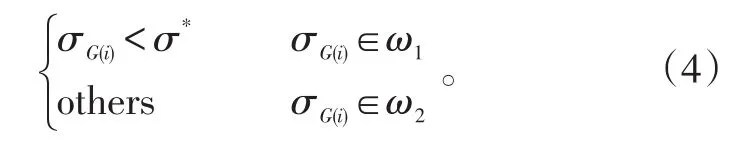
2 零速修正与改进算法的提出
在小扰动假设下,捷联惯性导航系统的系统误差模型如下[14]:

式(5)~(7)中:δφ为姿态角误差;δvn为导航坐标系内的速度误差;为导航坐标系内的位置误差;为导航坐标系相对惯性坐标系的角速度在导航坐标系下的投影;为姿态余弦矩阵;是陀螺仪的输出;为加速度计输出在导航坐标系内的投影;为地球自转角速率;为位置速率。
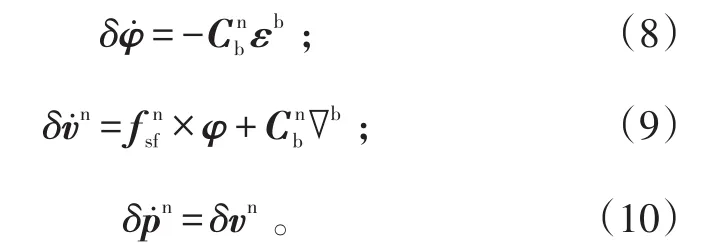
式(8)、(9)中:εb和 ∇b分别为陀螺仪漂移和加速度计零偏。
选取卡尔曼滤波的状态向量为导航参数误差,即由姿态误差、速度误差、位置误差组成的九维向量[16]
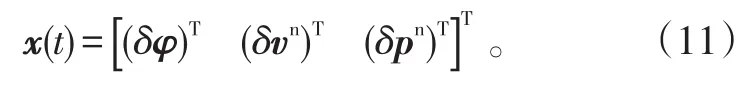
系统噪声由陀螺仪噪声和加速度计噪声组成的向量[17]:
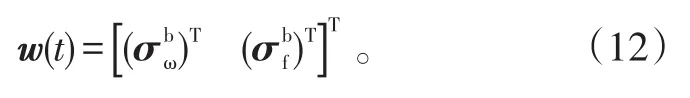
根据系统误差模型,卡尔曼滤波的连续状态方程可表示为:
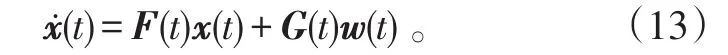
状态转移矩阵和噪声驱动矩阵分别为:
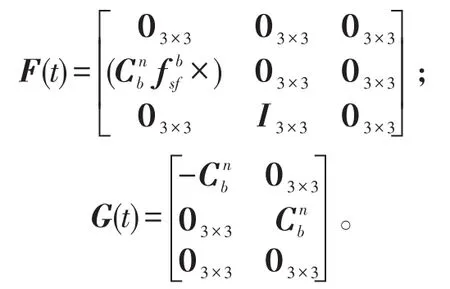
将零速区间内的真实速度认为是0,则零速区间内经导航解算得到的速度就是速度误差,将速度误差作为的伪观测值,可得到卡尔曼滤波的观测方程:

连续状态方程的离散化[18]:

惯性导航系统中,由于重力不确定误差和加速度计器件误差的影响,在纯惯性导航条件下,高度误差很快发散。以实验者A的10次八字形路径实验为例,见图1,在第40 s后,高度误差迅速增大,在经过仅仅2min的行走时间后,高度误差达到了2×104m左右。
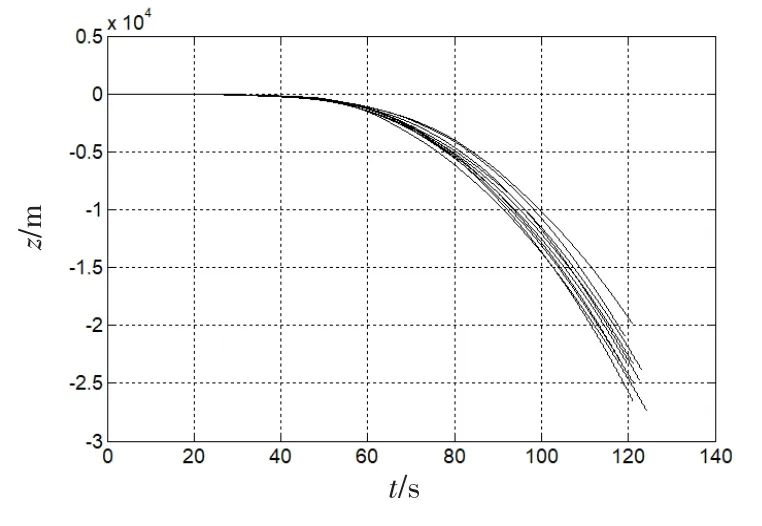
图1 纯惯导解算下高度估计图Fig.1 Height estimation by pure inertial solution
利用本节的零速修正算法对10次八字形实验导航参数进行校正,取零速检测阈值时,得到高度估计如图2所示。从图中可以看出,经过零速修正后,高度估计准确性大大提高,高度误差已经由原来的2×104m减小为6 m左右,高度估计图已经能够反映行走过程中脚步摆动。
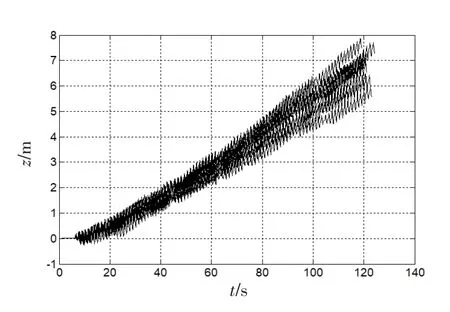
图2 本节零速修正解算下高度估计图Fig.2 Height estimation by ZUPT in this section
比较图1和图2可以发现,八字形路径实验实际为水平行走,高度不变,但是在纯惯导解算条件下,由于重力不确定误差和加速度计器件误差的影响,高度估计很快就脱离水平面,以很快的速度向下偏移,这与实际不符且最后误差太大。而通过本节的零速修正算法之后,从误差大小来看,高度误差比纯惯导解算条件下小很多,但是还存在误差;从高度估计的方向来看,通过本节零速修正算法之后,高度估计由纯惯导解算条件下的向下偏移,变为向上偏移。高度估计误差减小是利用零速区间的特性对导航误差周期性进行减小;而高度估计向上偏移是因为零速区间内对高度误差过度修正,导致高度估计偏向相反方向。于是,自然就提出这样的问题:是否能够通过控制高度修正的程度,来使得高度估计既不偏上,又不偏下,恰好能够反映实际行走高度的变化呢?答案是肯定的。
在本节提出的零速修正算法的基础上做部分改进,使高度修正与水平修正分开,从而方便控制高度修正的程度。由于上文提到的高度误差过度修正导致高度估计反而向上偏移,所以需要减小高度误差的修正程度,可以通过缩短高度修正的区间来减小高度误差的修正程度。图3为优化后的误差修正示意图,图中逻辑“1”表示零速区间,在水平修正区间对姿态角进行修正同时对速度和位置的水平分量进行修正,在高度修正区间对速度和位置的竖直分量进行修正。在这里只对零速修正模块的系统状态修正做部分修改,使水平通道与高度通道分开修正,仍然使用本节的状态方程和观测方程。用本文第1节的方法进行零速检测时,假设水平修正的零速判定阈值为,而高度修正的零速判定阈值为。

图3 优化算法示意图Fig.3 Optimization algorithm diagram
改进高度通道的行人导航算法只在系统状态修正的过程中分别修正水平误差和高度误差,而不重新设计设计滤波器。改进后,系统状态修正公式如下。
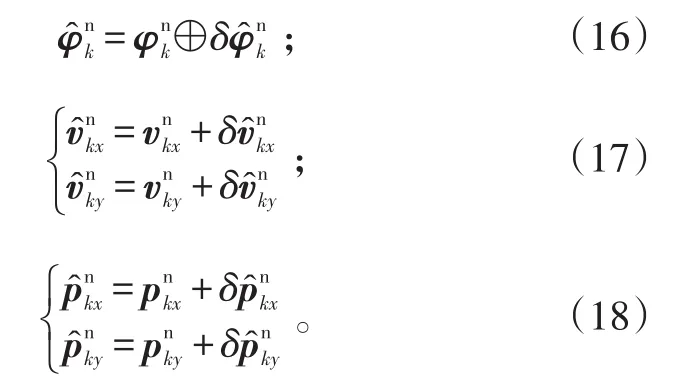

3 实验验证
利用改进高度通道的零速修正算法对第2节中的八字形路径进行解算,水平修正阈值。为了减小高度修正的程度,经多次试验,结果表明对实验者A而言,当高度修正阈值时,高度估计精度较高。得到的高度估计结果如图4所示。
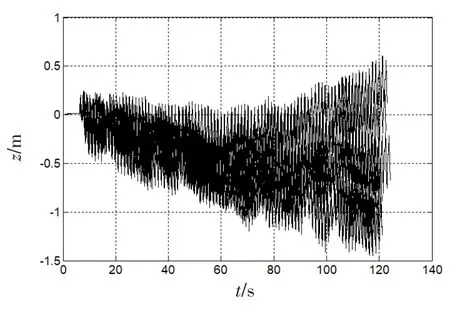
图4 改进高度通道算法高度估计图Fig.4 Height estimation by improved height channel algorithm
图4中可以看出,改进算法后,在2min的行走时间内,高度估计误差始终不超过1.5 m,并且高度估计能够很好反映行走时脚步的上下摆动,符合实际运动情景。与本节算法解算结果对比,可以发现改进后的算法减小了对高度误差的修正程度,使得原来过度修正算法得到优化,因此高度估计误差得以减小。
3.1 水平路径实验
为研究零速检测阈值对导航精度的影响,本文利用多种阈值进行零速检测并用检测得到的结果进行零速校正。在研究将水平误差和高度误差分开校正的过程中,发现对于实验者A而言,当高度校正阈值减小到水平校正阈值的一半左右时,高度误差校正能够达到较好的效果。图5为10次矩形路径和10次八字形路径实验,当取不同值时的水平误差图。
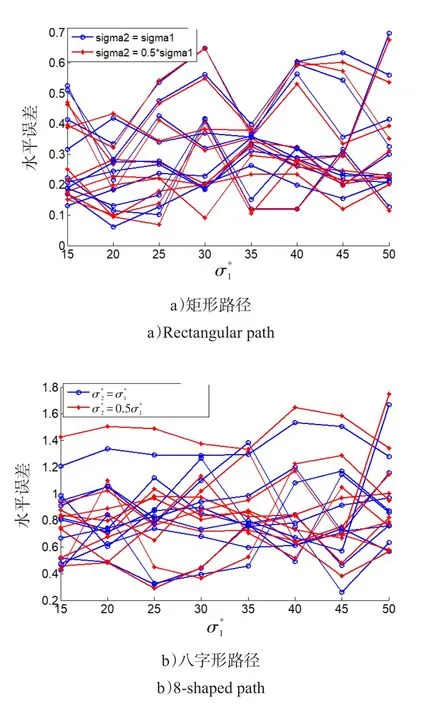
图5 水平误差图Fig.5 Horizontal error
图6表示实验者A的10次矩形路径和10次八字形路径实验,当取不同值时的高度误差图。
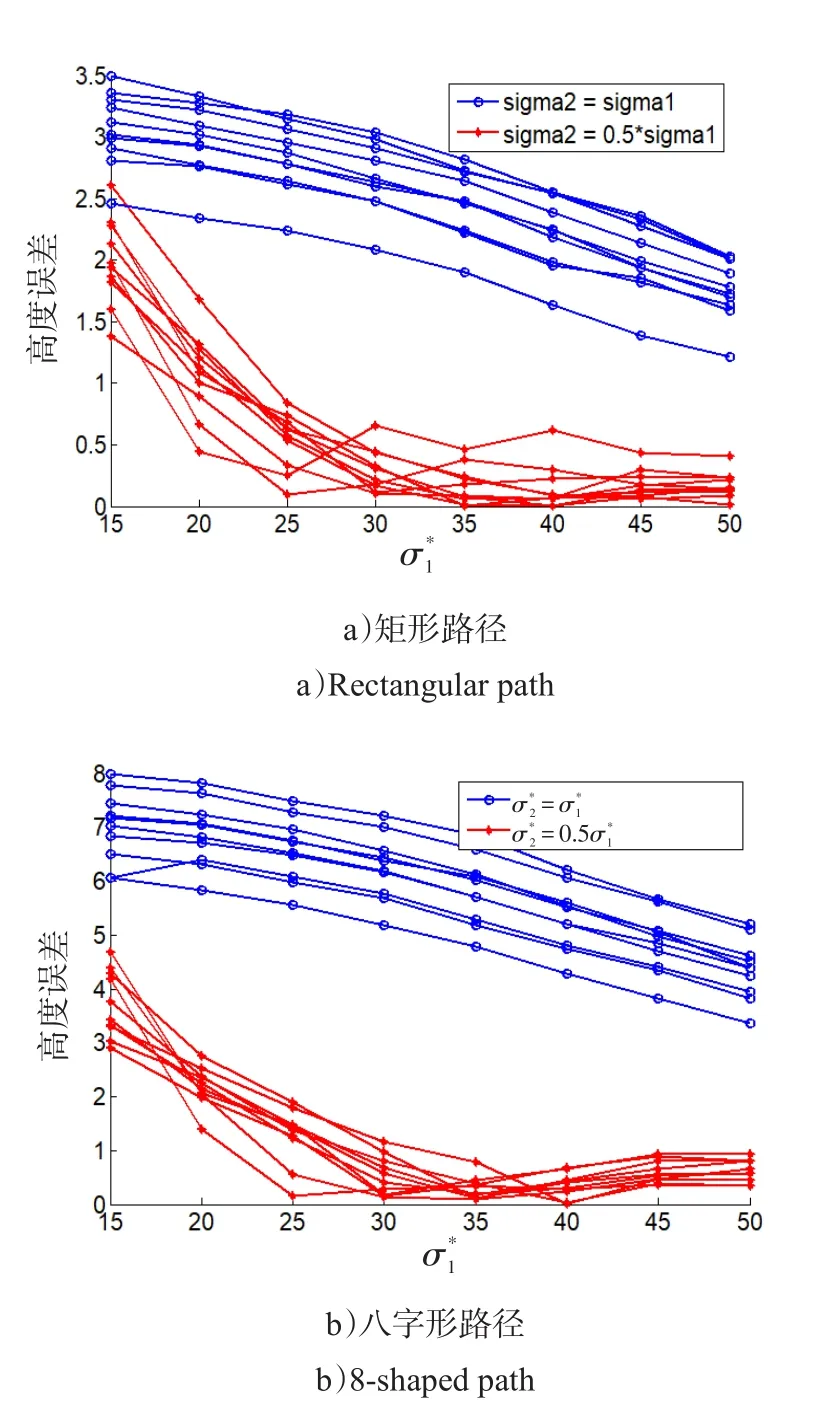
图6 高度误差图Fig.6 Height error
从横向来看图6,可以发现在选取的零速检测阈值范围内,高度误差随着阈值的增大而不断减小。从纵向来看,的关系对高度误差的大小产生了很大的影响,10次同样的实验,当利用进行解算时,高度误差相对于利用进行解算时大大减小。
表1分别表示不同零速检测阈值下,实验者A的10次矩形路径和10次八字形路径行走的平均高度误差实验结果。从表1可以看出,如果利用传统零速校正方法,在60 m和120 m的闭合路径行走实验中,分别产生了2 m和6 m左右的高度误差。而如果将高度校正阈值减小为水平校正阈值的一半,利用本文的校正方法,可以大大减小高度误差,当时,高度误差甚至减小为原误差的10%左右,高度估计误差减小为行走路程的0.5%左右。

表1 平均高度误差Tab.1 Average height error
3.2 上下楼梯实验
室内上下楼梯实验在大学综合实验楼进行,实验路径按图7所示的楼层示意图进行。
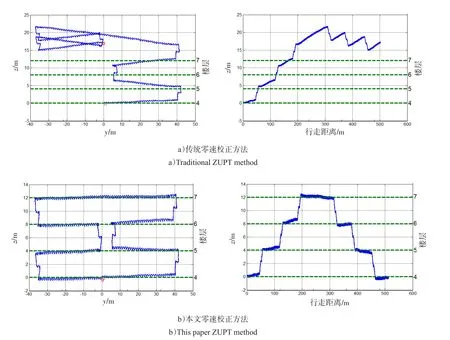
图8 上下楼梯实验高度估计图Fig.8 Estimation of the height of the up and down stairs
实验楼左右对称,中间为电梯间,电梯间两侧各有一个楼梯,在实验楼左右两侧还有一对楼梯。实验时将起点和终点设置在4楼电梯间的同一点,构成闭合路径。
该实验由2名实验者完成,每人进行3次重复实验。图8表示实验者A的一次实验结果图,其中左图为传统零速校正方法,将水平误差和高度误差同时校正,取时,得到的y/z图和距离/高度图;右图为本文提出的方法,将水平误差和高度误差分开校正,取时,得到的y/z图和距离/高度图,假设起始高度为0。
实验楼每层楼高4 m,比较2种方法的解算结果可以发现,传统零速校正方法解算得到的高度估计图完全不能反映实际的行走高度变化,而本文提出的零速校正方法解算得到的高度估计图能够很好反映实际行走过程中高度和楼层的变化,这为行人导航系统提供了较好的高度参考。
2名实验者进行的6次上下楼梯实验,得到的高度解算误差如表2所示。由于行走习惯的差异,适应不同行人的高度通道修正阈值不同,经过多次试验,在的情况下,适应实验者A的高度通道修正阈值为;适应实验者B的高度通道修正阈值为σ*2=13.5。

表2 上下楼梯实验高度误差表Tab.2 Height error of up and down stairs test
从表2可以看出,当利用传统零速修正算法进行解算时,实验者A的平均高度误差达到17.45 m,实验者B的平均高度误差达到15.79 m;而利用改进高度通道的零速修正算法进行解算时,实验者A的平均高度误差减小为0.73 m,实验者B的平均高度误差减小为0.97 m。该实验验证了改进高度通道的零速修正算法不仅在水平路径实验中对高度误差有抑制作用,而且在上下楼梯的立体路径实验中对高度误差也有很好的抑制作用;由于上下楼梯实验是由2名实验者完成的,实验结果表明改进高度通道的零速修正算法对2名实验者的高度误差均有很好的抑制作用,验证了改进算法并不仅仅适用于特定的行走习惯,具有普适性,可作为一种抑制高度误差发散的方法,用于其他可以进行零速修正的导航领域。
4 结束语
由于重力不确定和传感器器件误差的影响,在纯惯性导航系统中,很难对高度进行准确估计,高度误差会很快发散。惯性行人导航系统中。传统零速校正算法将水平误差和高度误差同时进行校正没有考虑到水平误差和高度误差的特性,无法更加有效地修正高度误差。本文在研究零速区间的区间长度对导航精度的影响时发现,使得高度误差达到最小的零速区间与使得水平误差达到最小的零速区间不一样,并且两个零速区间之间的关系对高度估计精度的影响很大。因此,本文设计了一种将水平误差和高度误差分开校正的算法,在零速检测的时候,划分出2个零速区间,并在这两个零速区间内分别进行水平误差和高度误差校正。经过大量实验验证,与传统零速校正算法对比,本文提出的算法能够充分考虑到各导航参数误差的特点,解决了纯惯性导航系统中高度误差的发散问题,大大提高了高度估计的精度,为行人导航系统提供了可靠的高度参考。本文首次提出将水平误差和高度误差分开进行校正,为零速校正提供了新的方法。
