间歇采样转发干扰对相位编码雷达的影响分析
2018-12-14陆洪涛郭慧峰
于 涛,李 宏,陆洪涛,郭慧峰
(中国洛阳电子装备试验中心,河南洛阳471003)
导弹突防过程也是导弹与雷达相互博弈的过程。脉冲压缩体制雷达能够解决传统雷达探测距离与分辨率之间的矛盾,成为现代雷达普遍采用的体制。相位编码信号是其常用的一种典型信号,通过伪随机码元序列对高频宽脉冲进行相位调制,对于传统干扰具有很强的抗干扰性能,且具有更低的波形截获概率。文献[1-3]研究表明,相位编码信号在检测性能和抗干扰性能等方面优于线性调频信号。
脉冲压缩雷达通过脉压处理,使得与雷达波形不匹配的干扰信号得不到压缩得益,因而传统噪声干扰须要提高功率才能达到干扰效果。近十年来,基于数字射频存储器(Digital Radio Frequency Memory,DRFM)的间歇采样转发干扰成为对抗脉冲压缩雷达的重要手段。通过文献可知,对线性调频信号的间歇采样干扰研究较多。文献[4]针对线性调频脉压雷达阐述了间歇采样转发干扰的数学原理和干扰效果,给出关键干扰参数和指标的数学表达式。文献[5]阐述了基于DRFM的干扰新技术,并研制了间歇采样转发干扰系统加以验证。文献[6]在间歇采样转发的基础上,叠加了移频干扰并对其效果仿真分析。文献[7-9]从仿真角度分析了相位编码信号间歇采样转发的干扰影响,表明相位编码间歇采样转发干扰只能产生一个假目标,这与线性调频信号间歇采样转发干扰不同。文献[10]从时域上推导了相位编码信号间歇采样转发经过匹配滤波器的输出响应,从原理上阐述了干扰效果。
本文对相位编码信号脉冲压缩网络进行建模,在文献[10]的基础上继续深入研究,详细分析了间歇采样转发干扰对相位编码脉冲压缩雷达的影响,分析了相位编码信号间歇采样干扰和经过匹配滤波器的时域输出响应。然后,研究了旁瓣抑制网络对干扰信号的影响。该机理研究为雷达对抗干扰评估试验提供重要的理论支撑。
1 原理分析
脉冲压缩网络主要由匹配滤波器和旁瓣抑制网络两部分组成,见图1。回波信号与间歇采样转发干扰信号一同进入匹配滤波器进行处理,然后经旁瓣抑制网络进入后续处理,本文研究这段的信号处理。
1.1 相位编码信号匹配输出
一般书籍资料中,对线性调频信号的匹配输出有较全面的推导,而对相位编码信号的匹配输出推导较少。本文以二相编码信号为例推导如下。
二相编码信号可以表示为:

式(1)中:φ(t)为相位调制函数,其值只有0和π;T为脉冲宽度;幅度a(t)取为常数1。
信号的复包络为矩形,信号可以表示为:

式(2)中:φm为第m个码元的编码值,取值为-1或1;p为码元个数;τ0为单个码元宽度;rect(x)为矩形函数,0≤x≤1时,rect(x)为1,其余为0。
二相编码信号的频谱为:

匹配滤波器单位冲激响应为h(t),表达式为:

式(3)中:s(t)为匹配滤波器输入端的信号;t0为白噪声中已知信号经过匹配滤波后信噪比最大的时刻,为了充分利用输入信号的能量,一般选择t0=T;将频谱进行归一化,常数c为1τ0。
则信号经过匹配滤波器后的输出响应为:

具体推导为:

因为有下式成立[11],
因此,
可以看出,2个矩形函数卷积为等腰三角形,峰值为τ0,中心点在t=T-(n-m)τ0处,三角形的底边长2τ0。这里假设T-t=kτ0+η,k为整数,0≤η<τ0。因此,当 -τ0< (k-n+m)τ0+η<τ0时,y(t)不为0。那么,由于 0≤η<τ0,所以,只有当k-n+m=0和k-n+m=-1时,y(t)不为0。
将n=k+m以及n=k+m+1代入到y(t),得:
其中,Rs为信号码元自相关。可以看出,相位编码信号经过匹配滤波器后输出y(t)为信号码元自相关序列的线性插值函数。对给定的一个时间t,首先根据t=T-kτ0-η,求出k和η;然后,将k和η代入上式即可求出y(t)。根据码元自相关函数Rs(0)最大,可反推出当t=T时出现压缩峰值。
同样,由表达式可知,|y(t)|极大值点(旁瓣峰值)只会出现在η=0的时刻,在η≠0的时刻只是线性插值,不会出现极大值点。
1.2 间歇采样干扰匹配输出
间歇采样脉冲信号p(t)是一个矩形包络脉冲串,其脉宽为τ,重复周期为Ts,即:
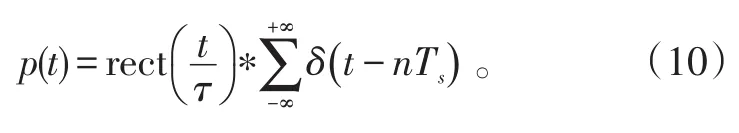
考虑到采样时长与码元宽度的关系,要求采样时长大于等于码元宽度的一半,即τ≥τ0/2。否则,无法采用二相编码信号的离散理论进行分析。
经过间歇采样后,信号可表示为:

am为采样码元的编码值,取值1或0,关键是确定am的值。根据采样时长τ、采样周期Ts以及码元宽度τ0的关系,am的取值可以分成3种情况:①码元完全处于采样时间内,am=1;②码元完全处于间歇时间内,am=0;③当采样结束时,一般会出现码元的一部分处于采样时间内,另一部分处于间歇时间内,此时做四舍五入近似处理,若码元的一半以上都处于采样时间内,则am=1,反之am=0。最后,间歇采样信号可以表达为:

式中,γm为间歇采样后的编码,取值为-1,1,0。其经过匹配滤波器后的输出响应为:

推导过程与前一节一致,结果可表示为:

Rsxs(k)为信号编码φm与间歇采样后的编码γm的互相关序列,输出响应为互相关序列的线性插值函数。对互相关序列进行分析,可推出当t=T时出现压缩峰值Rsxs(0),其幅度与间歇采样干扰信号的占空比τ/Ts有关,与码元序列无关。当占空比为50%(最大)时,γm中有50%的非零编码,50%的零编码。ys(t)峰值幅度为y(t)峰值幅度的一半。ys(t)的旁瓣位置与y(t)的旁瓣位置一致,其幅度受信号编码方式,采样周期和采样时长决定。与线性调频信号不同,相位编码信号经间歇采样脉压输出后不会出现主假目标和次假目标,而是形成一个假目标与一群旁瓣。
1.3 旁瓣抑制网络对信号的影响
脉冲压缩处理时必须降低距离旁瓣。否则,强信号脉压的旁瓣会掩盖或干扰附近的弱信号的反射回波。线性调频信号可以通过加窗方式很好地抑制旁瓣,但在相位编码信号分析上并不适用,可以通过采用其他方式进行处理,文献关于相位编码信号的旁瓣抑制方法主要有延时加权网络、最小均方逆滤波法、线性规划法、神经网络等,各种方法都是求得抑制网络加权系数,只是实现准则不同[12-14]。
前文讲到,相位编码信号脉压输出y(t)极值点一般出现在η=0时,在η≠0的时刻只是附近2个极值的线性插值,即极值点出现的周期为τ0。那么,可以用延时加权网络进行旁瓣抑制,加权网络见图2。

图2 旁瓣抑制加权网络Fig.2 Sidelobe suppression weighted network
加权网络由2N-2个延时线和2N-1个加权单元相加器组成,N为码元个数每节延时线的加权系数为β-N+1,β-N+2,…,βN-2,βN-1,延时时间为τ0。为减少未知量,网络可为对称网络,即β-k=βk(k=0,1,…,N-1)。加权网络的冲击响应可表示为:

回波信号输出响应为:

一般情况下,要求输出主瓣不变,旁瓣为0。主瓣的位置为Nτ0,式(16)可令t=Nτ0+mτ0(m=0,1,…,N-1),可得N个方程组成的方程组。求解加权系数,当码元个数较少时,即N较小,可以联立方程组求解;当N较大时,需要借助计算机计算加权系数,加权网络系数的求解最后归根于矩阵方程的求解,随着码元数目的增多,最麻烦的是系数矩阵的构建。通过分析,系数矩阵的构建与码元的自相关有关,具体可以通过折叠码元自相关得到,以一个码元为N的序列为例进行说明,它的自相关序列为2N-1个。首先,以中间的数据(即第N个数据)为中心进行折叠相加,从折叠后的数据选取前N个数据作为系数矩阵的第一行。接着,将中心前移,即以第N-1个数据为中心进行折叠相加,从折叠后的数据选取前N个数据作为系数矩阵的第二行。依次类推,直到构建系数矩阵的第N行。
须要说明的是,文献[15]中旁瓣抑制网络延时线为2τ0,因为对象为巴克码,其自相关存在周期性(周期为2τ0)的0出现。因此,对巴克码来说,旁瓣抑制网络延时线可以为2τ0,加权系数能够减少一半。但对于M序列码来说,自相关序列并不具有如此性质,因此本文的旁瓣抑制网络是一个建立在式(9)研究基础上的通用网络。
间歇采样干扰信号经匹配输出进入旁瓣抑制网络后的输出响应为:

βk为前文求得的加权系数,是针对y(t)而设计的加权系数。通过分析,y(t)经加权网络能达到主瓣不变,副瓣为零的目的。但由此得到的加权系数鲁棒性弱,当干扰信号经过时,并不能将干扰信号的旁瓣进行抑制,却可改变旁瓣的输出值,改变量跟码元序列与间歇采样序列有关。间歇采样转发干扰经过旁瓣抑制网络后依旧能够对雷达形成有效干扰。如何应对?这成为雷达抗干扰领域的一个研究热点[16-18]。
2 仿真分析与结果
本文分析了间歇采样转发干扰对相位编码脉冲压缩雷达的影响。为验证其正确性,采用Matlab数学仿真的方法进行验证。以127位M序列码为例,信号幅度为1,码元长度为 0.5 μs,信号总长 63.5 μs。首先,通过码元序列得到自相关序列;再由式(9)得y(t)的表达,理论计算与仿真输出如图3所示。

图3 信号理论输出与仿真输出Fig.3 Signal theory output and simulation output
从图3中可以看出,理论输出与仿真基本一致,压缩增益为码元数目,压缩峰值位置为63.5 μs处。旁瓣峰值与码元序列有关,位置只可能出现在距离脉压峰值nτ0(n的可能值为1,2,…,N)的位置上,具体位置同样与码元序列有关。
以前例数据继续分析间歇采样干扰的匹配输出,间歇采样周期为6.35 μs,占空比为50%,经匹配滤波器后的理论输出与仿真输出如图4所示。

图4 干扰理论输出与仿真输出Fig.4 Interference theory output and simulation output
图4中可以看出,理论计算的结果与计算机仿真结果吻合良好,峰值上稍有差别,主要是由于采样时间并不是码元宽度的整数倍,理论分析时对式(11)中am的取值问题造成的。而计算机仿真属于连续性分析,不存在离散性问题,其峰值为原来的一半。因此,峰值与间歇采样的占空比成正比。旁瓣位置还只能出现在距离脉压峰值nτ0(n的可能值为1,2,…,N)的位置上,其峰值略比图3有所升高。其变化与码元序列、采样时间、采样周期有关。
接下来考察旁瓣抑制网络对干扰信号的影响,回波信号与干扰信号经过加权网络的输出如图5、6所示。从中可以看出,相比图3,加权网络对脉压波形旁瓣抑制明显,主峰位置、幅度以及宽度均未受到影响,而旁瓣衰减至零。这与线性调频信号脉冲压缩后经过旁瓣抑制网络后的输出有很大不同。相比图4,干扰信号经过加权网络,主瓣的幅度略有下降,旁瓣峰值发生变化,加权网络并不能对间歇采样干扰信号进行旁瓣抑制,与前文分析相符。输出的旁瓣最大值与输入旁瓣最大值相当,具体数值依旧与码元序列、采样时间、采样周期相关。

图5 回波信号经过旁瓣加权网络输出Fig.5 Output of echo signal through sidelobe suppression network

图6 干扰信号经过旁瓣加权网络输出Fig.6 Output of interference signal through idelobe suppression network
根据本文研究,结合线性调频信号间歇采样形成的主次假目标特性,在不考虑重复转发的情况下,间歇采样对线性调频雷达更容易形成欺骗干扰,而对相位编码雷达更易形成压制干扰,因为产生的旁瓣相对于线性调频产生的假目标密度大得多。
3 总结
本文分析了间歇采样转发干扰对相位编码脉冲压缩网络的影响。分别推导了相位编码信号以及间歇采样转发干扰经过匹配滤波器的输出响应,可以发现间歇采样干扰信号能产生一个假目标与一群旁瓣。进而研究了旁瓣抑制网络对干扰信号的影响。结果表明旁瓣抑制网络可以有效抑制回波信号的旁瓣,而无法抑制干扰信号的旁瓣。干扰信号能够对相位编码雷达形成有效干扰。本文对于雷达对抗试验评估具有借鉴意义。
