一种带随机时延和丢包的分布式多传感器融合估计方法

陈红兵，王元鑫，赵国荣，卢建华，廖海涛

（1.海军驻南京地区航天机电系统军事代表，南京210006；2.海军航空大学，山东烟台264001）

无线传感器网络（WSN）革命性地改变了大规模建设分布式网络系统的能力。它能提供以前所未有的诸多信息的质量和数量，将彻底改变监控环境的能力[1]。以网络作为通信传输介质的闭环反馈控制系统称为网络控制系统（NCS），其优点是节约成本、便于实现资源共享、系统可靠性和模块性较高等[2]。两者的研究在近年逐渐成为学术界的一大热点。但是，它们也面临一些挑战，诸如传感器功率调度、路由选择、数据丢包补偿，数据压缩和编码等，考虑到传感器、执行器和控制器在物理上不共址并且通常由电池供电，需要通过无线通信网络交换信息。这些只是少数在数据收集应用中出现的问题，其目标是准确地重建传感器测量值。实时监控和控制应用又额外增加了难度，因为丢包和时延可能会降低决策部分的有效性。因此，评估数据的随机时延和丢包对整体系统性能的影响很重要。

目前，通信协议和网络控制系统是分开设计的。特别是协议基于保守启发式设计，指定了最大时延和最大丢包的阈值，但没有清楚地说明它们对全局应用性能的影响。在应用程序层面，控制系统并非专门设计用于利用有关通信协议的丢包和时延统计信息。无线传感器网络的环境监测如图1所示。

受这些因素的推动，本文的目标是研究最优传感器融合，其中测量值通过无线通信网络发送到单个当地中心，然后加以融合以获得系统状态的估计。每个传感器测量值受其自身随机延迟和可能性丢包的影响，因此根据每个传感器与集中式融合节点的距离来关联不同的数据包分布情况。

图1 无线传感器网络用于环境监测的示意图Fig.1 Schematic diagram of a wireless sensor network monitoring environment

1 目前进展

目前，多个小组研究了具有随机时延或丢包的网络控制系统。文献[3]很好地回顾了该领域的一些成果，可以分为2大类：第1类关注可变时延但不包含丢包；第2类关注丢包但没有时延。

在第1类中，Nilsson等[4]将LQG最优控制设计扩展到受随机测量值和时延影响的采样线性系统，并表明了最优控制器增益是如何与时滞相关的。但他们的工作仅限于共址的传感器和执行器。不同的是其他作者研究了从具有不同时延的传感器获得测量值的数据融合。如，Alexander[5]和Larsen等人[6]推导出次优但计算效率高的卡尔曼类滤波器来解释随机时延，并通过Monte-Carlo仿真器测试了它们的性能。Julier等人[7]研究了测量值时间戳不确定时的估计问题。

在第2类中，对应用最佳控制和离散时间系统估计作了相当大的努力。其中，测量值和数据包可以用某些不包含时延的概率分布来处理。这个框架等效于所有数据要么没有延迟要么延迟无限大。例如，文献[8-10]为独立同分布的伯努利通信网络提出了补偿技术并且为闭环离散时间系统导出了稳定性条件。Sinopoli等[11-12]和Imer等[13]专门研究最小方差估计和最优控制。总之，从研究的系统架构上来分，目前的丢包线性系统状态估计模型主要分为2种：传感器直接将量测通过随化丢包的信道传输给状态佑计器进行估计[14-15]；传感器对本地量测进行处理之后再通过随机丢包的信道传输给状态估计器进行估计[16-17]。

本文提出了一个概率框架来分析传感器融合。其中，来自多传感器的观测数据包受到任意随机时延和丢包影响。在此框架中，测量值需要在传感器端用时间戳标记，但是数据包在接收方可能爆发式或者无序到达。本文扩展了文献[18]之前只考虑单传感器的工作，该估计器结构独立于数据包到达统计数据，并且如果数据包的最大时延有限，则可以使用具有有限存储缓冲器的卡尔曼滤波器来实现。

2 问题描述

考虑如下线性离散随机系统：

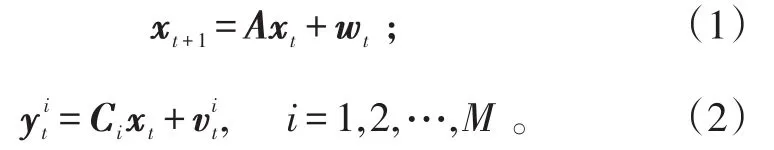
式（1）、（2）中：t∈N={0,1,2,…}；；；M表示多传感器的总数目。

此外，还假设对子(A,C)可观，(A,Q12)可达，且Ri＞0,∀i。测量值添加时间戳后封装成数据包，然后通过数字通信网络（DCN）传输，达到将数据包从源头传送到终端的目的。测量值的时间戳能对接收器端收到的乱序数据进行重新排序。现在的数字通信网络通常非常复杂，并且其架构和执行器依据所使用的介质（有线，无线，混合）和它们用于服务的应用（实时监控，数据提取，媒体相关等）而变化多样。研究中，将DCN建模为传感器和融合中心之间的模块，观测值向估计器传输时可能带有随机时延，该模型将时延无限大的情况视为丢包。假设准确传递到估计器端的所有观测数据包都存储。

在无限缓冲区中，如图2所示，图2a）为通用到达情况，图2 b）为具有有限缓冲区的情况。到达过程通过随机变量来建模，定义如下：

图2 最优卡尔曼估计存储器示意图Fig.2 Schematic diagram of optimal Kalman estimation memory

如果在t时刻估计器没有接收到观测值，假设在存储缓冲区的i,k槽存了零值，如图2所示。t时刻存储在估计器缓冲区的i,k槽中的值可表示如下：

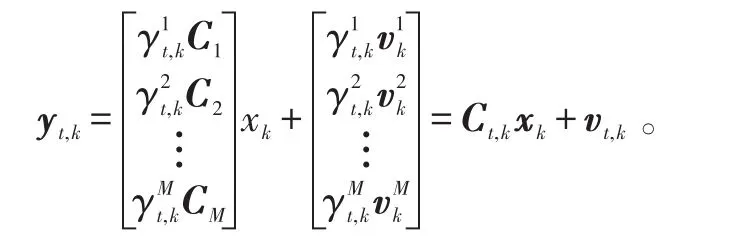
目标基于所有时刻t之前到达传感器融合端的测量值，得出最优均方意义下的估计器：

重要的是，要标记含有以上信息的估计器是否已发送，并且它不等同于计算。实际上，后者会将缓冲区的诸多零值视为真实的测量值而不是虚拟变量，从而导致性能降低。估计器的误差和误差协方差表示如下：

3 最小误差协方差下的估计器设计

在本节中，通过式（6）来计算最优估计器。首先，定义以下变量：

注意到在时刻t，由式（5）得到的估计器可用信息可以写成以下系统的输出：

对任何固定时刻t，这个系统可以看作一个关于时刻k的线性时变系统。其中，唯一的时变元素是观测矩阵Ct,k和测量噪声协方差Rt,k。

下面介绍本节的主要定理：

定理1：考虑式（1）、（2）给出的随机线性系统，其中Ri＞0。同时考虑由式（3）定义的到达过程，以及式（6）定义的均方估计器。设，该向量仅包括时刻t在传感器融合端出现的测量值，即从yt,k中去除虚拟零观测值获得的向量。类似地考虑矩阵，去除其中与虚拟零测量值相对应的所有零行。可以得到：

式（12）～（14）中，k=1,2,…,t。

式（17）～（19）中，k=t-N+1,t-N+2,…,t。

卡尔曼增益Kt,t和估计误差协方差Pt,t是时变的，因为它们取决历史到达的数据包γt。与收敛到稳态的标准卡尔曼滤波器不同，在考虑随机时延和丢包的情况下，该滤波器具有强时变性，由于矩阵的求逆而使其计算效率较低。

到目前为止，对数据包到达过程没有做出任何假设，其可以是确定性的、随机的或者时变的。然而，从工程角度来看，重要的是基于误差协方差Pt+1,t来评估估计器的性能。当数据包到达过程随机时，误差协方差也是随机的。在这种情况下，通常用预期误差协方差度量性能，即Eγ[Pt+1,t]，其中期望是相对于到达过程计算的。即使是简单的伯努利到达过程，目前尚不清楚是否可以分析计算Eγ[Pt+1,t]，只能获得上限和下限[10]。不去界定时变最佳估计器的性能，我们将集中讨论具有与图2b）的M×N缓冲器中的每个槽相关联的带有一组常数增益的融合滤波器，即对于所有的i=1,2,…,M和h=1,2,…,N-1的。然后，优化以实现稳态下的最小误差协方差。使用常值增益的优势是根本不需要像最优时变滤波器那样对任何矩阵求逆，因而适用于在线应用。此外，具有恒定增益的滤波器必然是次优的。因此，对于它们误差协方差的计算本身就有用，因为它提供了由式（11）～（14）给出的最小误差协方差意义下最优滤波器的误差协方差的上限。

假设数据包到达估计器端的过程平稳且服从独立同分布，其概率函数为：P[τt≤h]=λh，其中t≥0，0≤λh≤1在h=0,1,2,…非递减，且λh如式（4）定义。

变量λh对应于在h时间步长之前采样的数据包到达估计器的概率。显然，λh必然非增，因为λh=P[τt≤h-1]+P[τt=h]=λh-1+P[τt=h]。

将丢包概率定义为λloss=1-sup{λh|h≥0}。对时延的概率密度也可用由式（4）定义的到达过程来定义。实际上根据定义，对于h≥1，有P[τk=0]=λ0，P[τk=h]=λh-λh-1，并且P[τk=∞]=λloss。

最后，定义了数据包到达的最大时延：

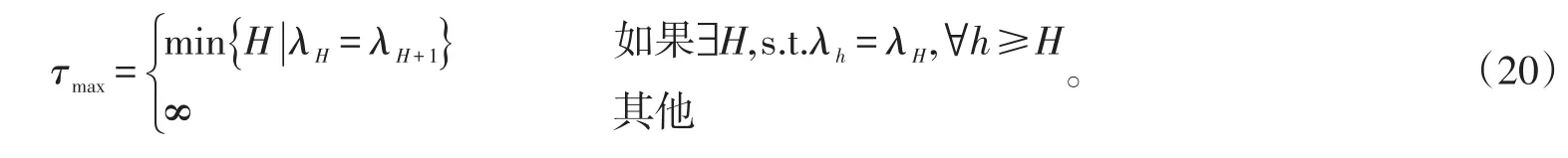
还假设不同的传感器具有不同的时延分布，即对于i=1,2,…,M，有。这对无线传感器网络是很自然的假设。实际上，如图1所示，远离融合端的传感器节点i比传感器节点j具有更大的时延和更高的丢包率。事实上，节点i需要多跳而节点j只需单跳到达接收端。

4 算例仿真与分析

系统状态初值x0由2个分量组成，且均在区间[-1,1]上均匀分布。。

选择无线通信网络动态系统的数据包时延概率函数：

为对比不同丢包率为系统性能的影响，上式中最大时延L依次取为13、14、15，则时延过程当中丢包的概率依次为0.35、0.3、0.25，图3以L=15为例。

图3 L=15时延概率函数Fig.3 Delay probability function atL=15

最优分布式融合估计的仿真结果如图4～6所示，2条曲线依次代表状态分量的真值和最优分布式融合估计值，可以定性看出融合估计值与真值相比，随着丢包率的减少融合估计的效果越来越理想，体现出丢包对系统融合估计的影响。

图4 L=13状态真值和融合估计值的轨迹Fig.4 Trajectory of state truth value and fusion estimate atL=13

图5 L=14状态真值和融合估计值的轨迹Fig.5 Trajectory of state truth value and fusion estimate atL=14

图6 L=15状态真值和融合估计值的轨迹Fig.6 Trajectory of state truth value and fusion estimate atL=15

图7中，当时延上限L=13依次增加到L=15时，即丢包率变低时分布式融合估计误差协方差矩阵Pt,t的迹Tr(Pt,t)的计算结果，由图7可知，在达到平稳时，Tr(Pt,t)随着丢包率的减小而减小，仿真表明数据传输时丢失越少，融合估计的误差越小。

图7 时延上限L与Tr(Pt,t)的关系Fig.7 Relationship between the maximum random delayLandTr(Pt,t)

5 结论

本文基于单点分布式传感器获得的一系列测量值，提出了最优化设计传感器融合估计的框架，表明最优滤波器是一个含有缓冲区的时变卡尔曼滤波器，其计算效率较高，因为它只需要有限的存储缓冲器。对于这类过滤器，如果每个传感器的数据包到达过程是独立同分布的但概率分布不同且丢包率充分小的情况小，则估计器是均方稳定的。

今后的工作，将利用最流行的无线传感器网络路由协议，来获得实验数据包到达分布情况，以评估使用本文所提工具进行在线监测应用的路由协议性能。