空间几何体的表面积与体积的计算

■邹弘毅

多面体的侧面积是所有侧面的面积之和,多面体的表面积是侧面积与底面积之和。解题时,要掌握柱、锥、台和球的表面积与体积公式。下面介绍几种计算空间几何体的表面积与体积的方法,供大家参考。

一、公式法

例1 已知圆柱的上,下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为____。

解：由题意可设圆柱的底面直径为2R,则高为2R。由过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,可得4R2=8,解得R=2。故该圆柱的表面积为π(2)2×2+22π×22=12π。

评析:解答本题的关键是求出圆柱的底面半径和高。

二、等体积法

例2 如图1,直三棱柱ABC-A1B1C1的各条棱长均为2,D为棱B1C1上任一点,则三棱锥D-A1BC的体积是____。

图1

解：由题意可知,直三棱柱ABC-A1B1C1为正三棱柱。由D为棱B1C1上任一点,可得S△BCD=×2×2=2,点A1到平面BCC1B1的距离d=。评析:本题考查棱柱的结构特征,考查利用等体积法求多面体的体积的方法。

三、构造法

例3 如图2所示,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则三棱锥P-DCE的外接球的体积为____。

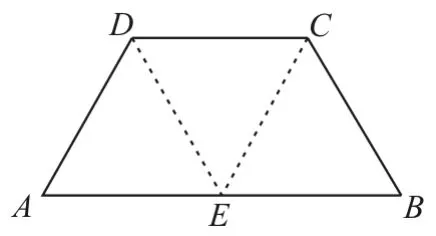
图2

解：由题意可知折叠后的三棱锥P-DCE是正四面体,它的棱长为1,由此正四面体可构造正方体,如图3所示。

图3

评析:通过构造正方体(或长方体),可把分散问题集中在一个特殊的空间几何体中,使得所求问题更直观化、简单化。