基于预瞄理论的智能驾驶客车轨迹跟踪控制方法研究

谢勇波, 李 熙, 朱 田, 冯 拔

(湖南中车时代电动汽车股份有限公司， 湖南 株洲 412007)

智能驾驶汽车在各个领域都具有广阔的应用前景[1]，轨迹跟踪控制技术是智能驾驶技术中的基本问题[2]。目前，针对智能驾驶车辆的轨迹跟踪问题，国内外许多科研机构都展开了广泛的研究。在轨迹规划方面，轨迹的表达方式多种多样[3-8]。在轨迹跟踪控制技术中大多采用基于模型预测理论方法[9]和基于最优预瞄理论方法[10]，然而这两种方法都存在局限性。

基于上述方法的局限性，本文提出一种基于预瞄理论的增量式轨迹跟踪控制方法，与常规增量式PID控制方法进行对比，结果表明，本文所提出的方法具有更好的性能。

1 车辆轨迹模型

车辆路径跟踪问题从根本上讲是一个方向控制问题，即为车辆的侧向控制。它以车辆前进方向的期望路径为基础，生成合理的方向盘转角来实现精准路径跟踪。

本文研究的对象是12 m城市客车，车速低于30 km/h，中低速控制不仅是高速控制的基础，在各行各业中也有广泛的用途，如机场摆渡车、城市客车、环卫车、景区车及矿车等[11-12]。在此工况下，本文采用基于阿克曼转向的几何方法作为车辆模型进行位置估计。

由阿克曼转向原理可知：

R=L/tanδ

(1)

式中：R为车辆的转弯半径；L为车辆的轴距；δ为方向盘转角。

假设当前时刻车辆位置及航向角为(xk,yk,φk)，下一时刻为(xk+1,yk+1,φk+1)，那么(xk,yk,φk)与(xk+1,yk+1,φk+1)将存在式(2)的关系：

(2)

式中：vk为车辆速度；δk为方向盘转角；ΔT为时间差。

在式(1)所示的模型中，需要测量车辆系统的角度传动比γ和车辆的轴距L。通过查找整车参数表可以获取车辆的轴距，角传动比通过式(3)得到：

γ=δ/δf

(3)

式中δf为前轮偏转角。

以车头安装GPS系统处为坐标原点，以车辆的正前方作为坐标X轴，以车辆的正左方作为坐标的Y轴，以车辆的正上方作为Z轴，定义车辆坐标系。

假设在规划周期内，速度保持不变，车辆的行驶行为完全由行驶路径来决定。车辆的横向加速度连续，行驶轨迹可由式(4)表示：

Y(X)=a0+a1X+a2X2+a3X3

(4)

通过上面建立的坐标系X0Y可知，初始状态下车体方位和质心均为0，它满足式(5)的约束：

(5)

由式(5)可确定：

a0=a1=0

(6)

车辆出现换道行为时，车辆质心坐标改变为(Xc,Yc)。由终点目标航向角θ的约束关系可知：

(7)

由终点偏移量yoffset的约束关系可知：

Yccosθ+Xcsinθ=yoffset

(8)

车辆行驶轨迹满足如下关系：

(9)

联合式(7)、(8)、(9)，可得：

(10)

在速度确定的前提下，由式(10)可知，终点坐标Xc和终点航向角θ可以确定唯一的轨迹路径。

通过式(10)，可以将轨迹确定下来，对期望轨迹的实时滚动优化，既可以消除横向的位置偏差，也能保证行车路线安全可靠。

2 基于自适应滚动预瞄纵向解耦控制方法

智能汽车的轨迹跟踪控制包括侧向控制和纵向控制，其中，车辆的纵向控制可通过调节车速来实现。

2.1 预瞄模型

本文基于驾驶员特性，研究驾驶员-汽车闭环系统，结合预瞄模型来估计方向盘的输入响应。预瞄模型的基本规则如下：

假设在任何时刻，驾驶员都注意前方距离为d。预瞄距离的计算公式如式(11)：

l=vrTp

(11)

式中：l为预瞄距离；vr为车辆的实时速度；Tp为预瞄时间，令Tp=1.2 s。

结合期望轨迹，在轨迹上寻找采样点坐标，来满足预瞄距离，计算公式如式(12)：

(12)

式中：(xd,yd)为采样点坐标；θd为采样点位置的期望航向角。

2.2 预估模型

图1是预测算法的简化模型。

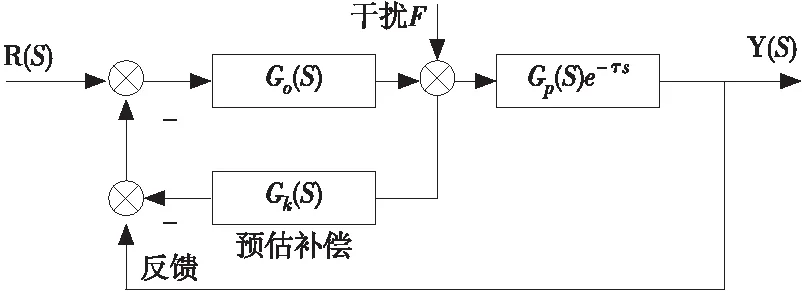
图1 预测算法的简化模型

假设智能驾驶车辆的纵向速度与前轮速度近似，则车辆在一个控制周期的航向变化量Δφ近似计算如下：

Δφ=vT/R

(13)

式中T为控制器的采样周期。

前轮所经过的中心点半径R的计算如下：

R=L/sinδf

(14)

将式(14)代入式(13)可得：

Δφ=vTsinδf/L

(15)

2.3 控制算法

针对大惯性智能驾驶客车的特点，本文提出一种横纵向解耦控制方法，能保证控制结构得到简化，同时能提高控制的精度。

智能驾驶客车横纵向解耦控制框图如图2所示。

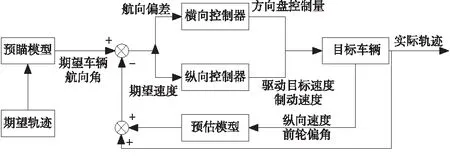
图2 智能驾驶客车横纵向解耦控制框图

车辆前轮的实时航向角θ的计算公式如式(16)所示：

(16)

式中：θh为GPS实时反馈的航向角；δs为方向盘转角反馈；k为方向盘角度与车辆前轮偏角的比例系数。

经过计算，方向盘转角角度与车辆前轮偏角的比例系数为23.1。

为了保证控制精度，本文设计一种预估控制模型，来准确预测车辆的航向变化趋势，其模型的表达式如式(15)。因此，车辆的前轮预估航向角θr可通过式(17)计算得到：

θr=θ+Δφ

(17)

前轮航向角的偏差量e可通过式(18)计算得到：

e=θd-θr

(18)

前轮航向偏差对应的方向盘转角变化量Δu可通过式(19)计算得到：

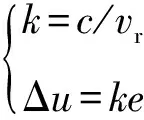
(19)

式中：k为航向偏差对应方向盘转角变化量的比例系数；c为常量，经试验可以测得c=24。

输出的方向盘控制量u可通式(20)计算得到：

u=δs+Δu

(20)

输出的方向盘控制量u存在式(21)的约束关系：

umin≤u≤umax

(21)

式中：umin为正常情况下方向盘转角的最小限度；umax为正常情况下方向盘转角的最大限度。

2.4 自适应滚动预瞄纵向解耦控制器设计步骤

基于智能驾驶客车，本文提出了一种横纵向解耦控制方法，在每个采样周期内，建模步骤如图3所示。

图3 横纵向解耦控制方法流程

3 仿真分析

3.1 基于预瞄的三次多项式轨迹生成结果

在选择预瞄距离的同时也需考虑道路的曲率和车辆的速度，道路曲率从高精度地图上获得，预瞄距离和道路曲率成反比例关系，随着曲率的增大而适当减小。在较大车速时，应选择较大的预瞄距离，在较小车速时，应选择较小的预瞄距离，距离选择为当前车速下2 s内所经过的距离。

在预瞄距离确定后，选择轨迹终点位置，基于三次多项式生成轨迹仿真效果图如图4所示。

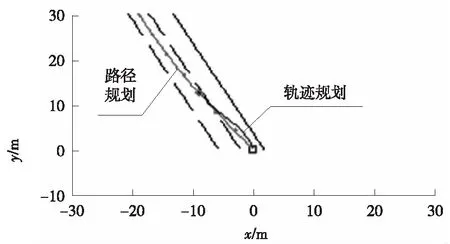
图4 换道轨迹生成图

3.2 基于TruckSim的Simulink模型和结果

TruckSim软件是由美国机械仿真公司开发的一款工业仿真软件，多用于轻型货车、大客车等车辆的仿真及分析。

本文对车辆的质量、尺寸以及绕各转动轴的转动惯量进行整车建模。在TruckSim仿真界面上对应设置车辆实际配置参数，保证整车模型的搭建与实际情况相同。

结合式(10)，在恒定的速度下，车辆控制器仅控制方向盘转角，控制效果如图5所示。图中期望轨迹用实线表示，车辆在进行横向控制时的实际行驶轨迹用“×”表示。从图5可知，基于自适应滚动预瞄的控制方法具有很好的鲁棒性和实时性，可以有效预测弯道跟踪情况。

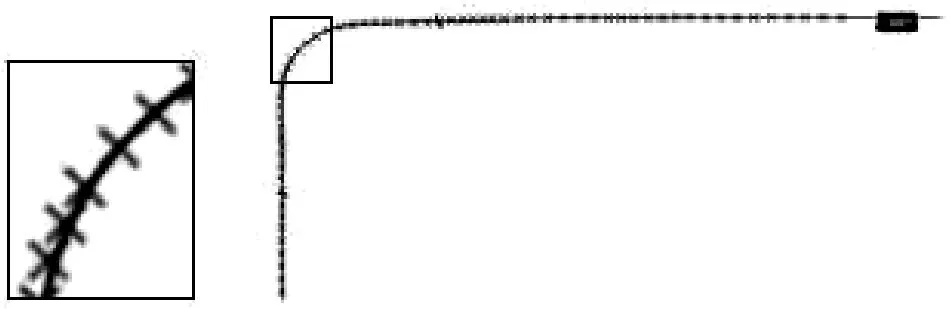
图5 直角弯横向控制效果图

横纵向联合控制效果图如图6所示。图中期望轨迹用实线表示，车辆进行横向控制时的实际行驶轨迹用“×”表示。从图6可知，在增加纵向速度控制的条件下，应用基于预瞄的自适应轨迹跟踪控制仍然可以达到很好的轨迹跟踪性能。

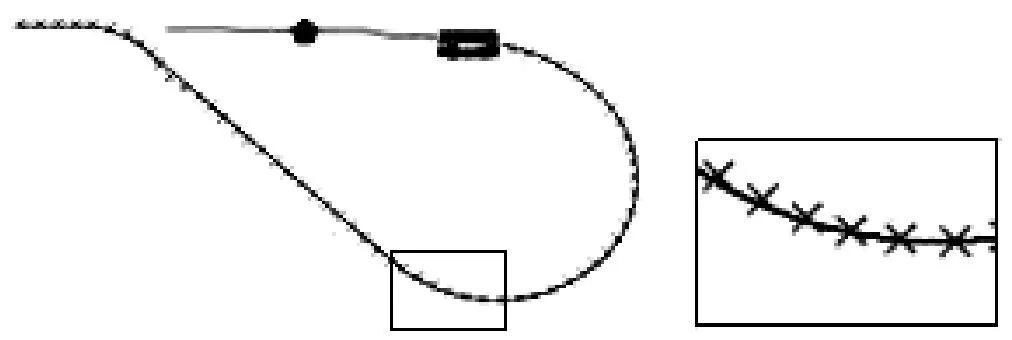
图6 横纵向联合控制效果图

因此，在实际情况下，本文所设计的智能驾驶横纵向解耦控制方法对于大惯性智能电动客车控制具有可操作性，能够有效消除车辆的大滞后和大惯性带来的影响，保证了控制精度。

3.3 对比分析

采用增量式PID方法与本文所提出的基于预瞄理论的轨迹跟踪控制方法进行对比，对比分析时保证其设置参数相同。

图7为基于预瞄理论的轨迹跟踪控制方法，图8为增量式PID控制方法。

图7 基于预瞄的轨迹跟踪控制器原理图

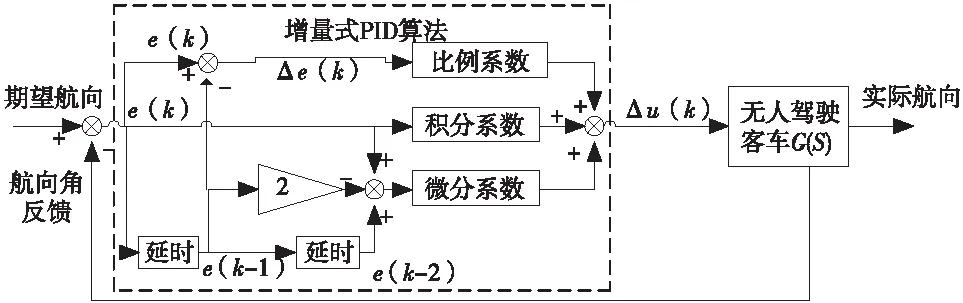
图8 增量式PID控制器原理图

在车速25 km/h的情况下设置航向初始偏差为20°(0.35 rad)，在Matlab平台下进行系统仿真，阶跃响应结果对比如图9所示。

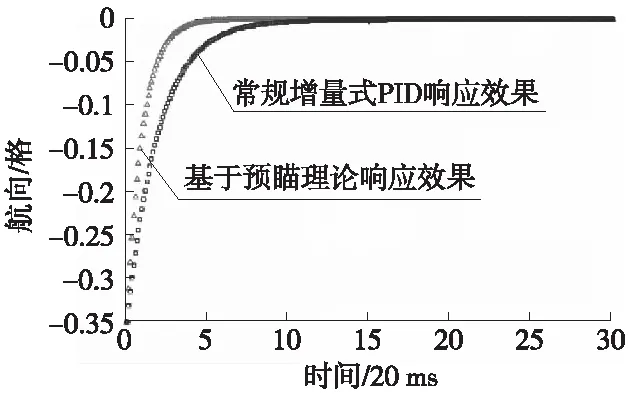
图9 阶跃响应实验仿真结果对比图

从图9中可知，和常规增量式PID控制器相比，基于预瞄理论的轨迹跟踪控制方法阶跃响应更快，不仅达到稳态所需的时间更短，而且也具有更好的泛化能力和鲁棒性。

4 结束语

本文研究了一种基于预瞄理论的轨迹跟踪控制方法，从研究结果可知，所设计的轨迹跟踪控制方法与全局路径规划方法都具有良好的性能，通过实车环境也验证了所提方法的可行性。此研究针对中低速客车有效，针对高速情况还需要在后续的研究中试验和验证。