基于初值估算和潮流可控范围的UPFC潮流收敛特性研究

李生虎，汪 婷，吴 东，张 浩

(1. 合肥工业大学 电气与自动化工程学院，安徽 合肥 230009；2. 国网天津市电力公司检修公司，天津 300232)

0 引言

作为一种柔性交流输电装置，统一潮流控制器UPFC(Unified Power Flow Controller)在美国、韩国和中国得到越来越多的应用[1- 4]。UPFC综合可控串补和可控并补的优点，同时调节母线电压和线路潮流，从而可改善电网潮流分布，提高系统可靠性[5- 6]。

精确潮流建模是UPFC参与电网安全运行控制的前提。文献[7-10]将电网与UPFC变量分开，无需考虑其初值，但是忽略了UPFC结构和控制特性，实用价值有限。文献[11]采用最优潮流模型，建立目标函数对UPFC变量的灵敏度，基于灵敏度更新UPFC变量，将优化和潮流计算迭代求解，计算量较大，且UPFC采用功率注入模型，过于简化。文献[12]将UPFC控制目标和电网潮流约束统一迭代，控制线路有功、无功和节点电压任意组合，算法较为实用。相比独立串补和并补装置，UPFC的结构和控制较为复杂，其潮流收敛性较差，原因如下。

a. 对变流器电压初值敏感。由于UPFC串联等效成电压源相角范围为0～2π，会使收敛性变差[13]。文献[12]根据UPFC控制目标对变量初始化，但是串联变流器电压相角初值的选取可能使得潮流收敛到实际不可行解。目前还未发现文献提出实用公式或经验值来选择UPFC变量初值。

b. UPFC潮流目标不合理。考虑到电网安全和变流器容量有限，当受控线路潮流设置过大时，实际不能实现控制目标，潮流解发散，或者串联变流器电压超过允许上限。因此需要基于给定运行方式，确定潮流可调范围。文献[14-15]求解UPFC的潮流控制范围是一个圆域，圆心是加入UPFC前受控线路潮流，半径与串联电压幅值最大值、受控线路受端节点电压成正比，与其电抗成反比。但前提条件是受控线路两端电压幅值不变，忽略了控制目标对潮流分布的影响[16]。如何根据变流器容量和实际运行场景量化UPFC潮流控制范围并引入潮流约束，未见相关文献详细阐述。

本文提出基于初值预估的两阶段潮流算法，任取变量初值进行常规潮流计算，对所得UPFC串联变流器电压相角进行估算，将其作为第二阶段潮流初值，以解决变量初值敏感问题。然后利用拓展雅可比矩阵建立UPFC串联控制变量对潮流控制目标可调范围的灵敏度模型，以量化串联变流器电压对潮流控制范围的影响，避免因潮流目标值设置不合理引起潮流发散或串联变流器电压超出上限。以IEEE 14节点系统为例，验证了所提算法的正确性。

1 基于初值预估的两阶段潮流算法

1.1 UPFC潮流约束

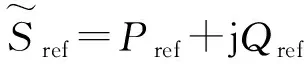
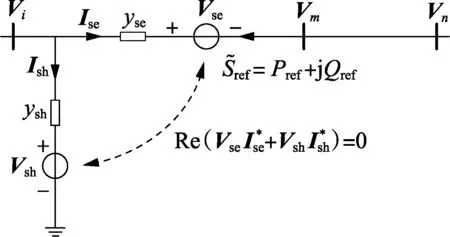
图1 UPFC等值电路Fig.1 Equivalent circuit of UPFC

串联变流器控制线路潮流，并联变流器维持直流支路有功平衡、控制节点i电压，节点i为PQV类型。新增潮流约束方程有：

(1)

(2)

(3)

1.2 串联变流器电压相角的估算

在常规潮流平电压启动的基础上，文献[12]给出了UPFC变量初值算法：

(4)

(5)

(6)

(7)

(8)

其中，上标(0)表示初值；Vref为并联变流器控制目标。

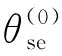
图2 串联电压相角可能解Fig.2 Possible solutions of θse

θse可能取值情况如图2所示。在[-π，π]周期内会出现2次sinθse、cosθse数值相等但符号相反的情况，如图2中的①和②。假设①处相角为θse，对应Vse>0，将②处θse+π代入式(9)，可得Vse<0，该结果不符合实际运行情况。需要说明的是，式中除串联电压外，其他电压相角、幅值均不变。

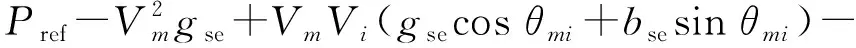
VmVse(gsecosθmse+bsesinθmse)=0

(9)

其中，θmi=θm-θi，θmse=θm-θse。

若正确解在①处，而初值接近π/2，与①相比较，②更接近所求初值，迭代后潮流结果可能误收敛于幅值小于0的②处，实际不可行。另外，三角函数具有周期性，当θse初值与正确解相差较大，甚至可能收敛于③、④处，相角在区间[-π，π]以外。

将θse结果分成3类如表1所示，其中k为整数。由此可对θse进行估算。对于第2或3类结果，可将相角进行2kπ或(2k+1)π相位变换，直到满足相角约束，变换后的相角就是在该潮流控制目标下串联变流器所需要调整的电压相角。

表1 串联电压相角分类Table 1 Classification of θse

1.3 基于初值预估的两阶段潮流算法

受控线路潮流调整与电网网络结构、线路位置有关，无法直接给出潮流控制目标值与串联电压的解析表达式，需要常规潮流才能估算串联电压，因此提出基于初值预估的两阶段潮流算法，如图3所示，包括以下步骤。

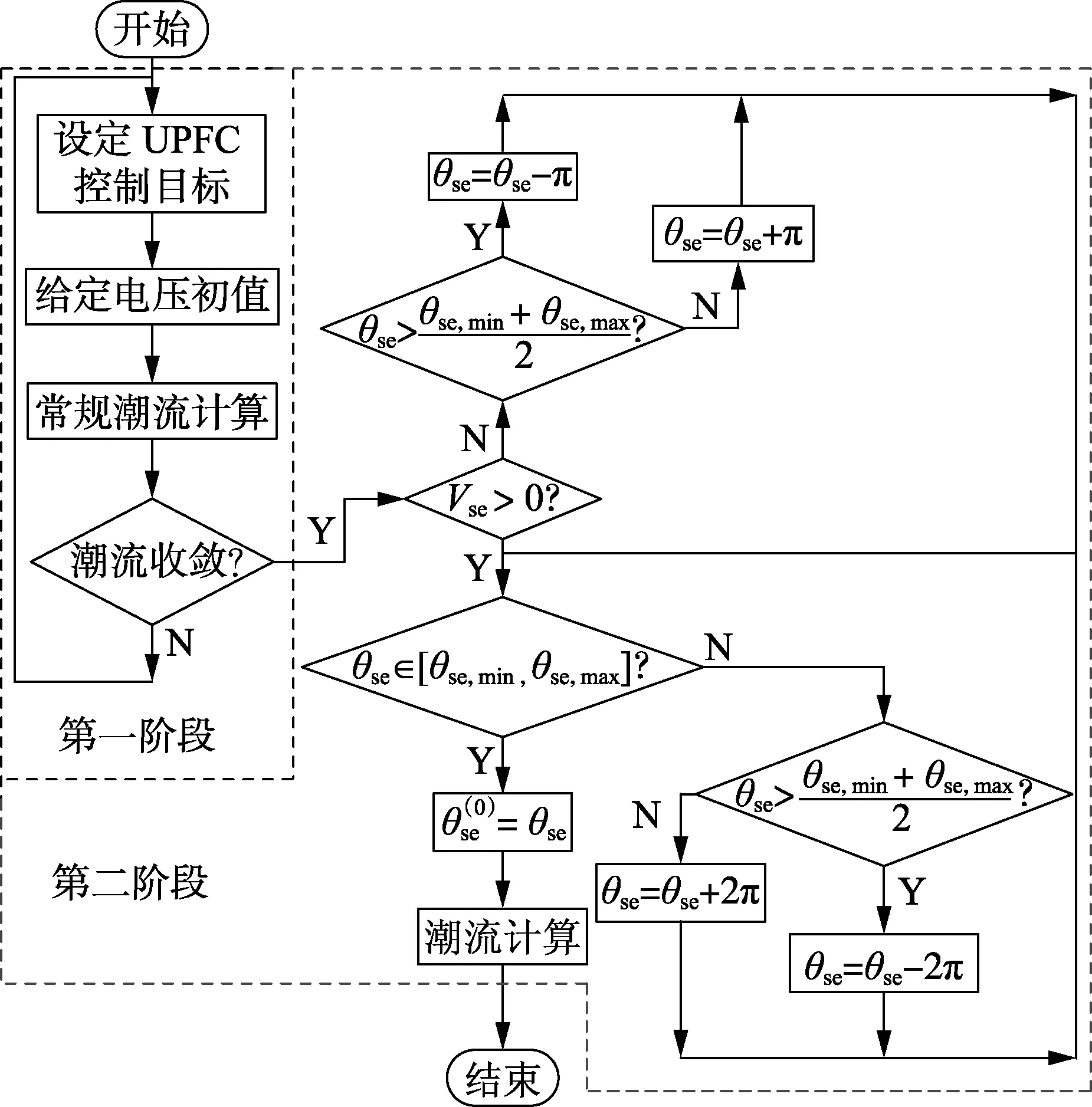
图3 两阶段潮流算法流程Fig.3 Flowchart of two-stage power flow algorithm

a. 确定UPFC控制目标设定值。

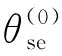
c. 统一求解潮流，若收敛，则转步骤d；否则返回步骤a，调整潮流控制目标。

d. 若串联电压幅值Vse>0，则转步骤e；否则，转步骤f。

e. 判断θse是否在取值范围内，若是转步骤g；否则，令θse=θse+2kπ，直到满足相角约束，转步骤g。

f. 令θse=θse+(2k+1)π，直到θse在取值范围内，转步骤g。

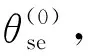
2 基于灵敏度模型估计UPFC潮流控制范围

对可控串补、可控并补潮流灵敏度的研究[17-18]为量化UPFC潮流控制范围提供了参考思路。基于UPFC与电网联立的潮流方程，可基于拓展雅可比矩阵构造控制目标与受控参数的灵敏度。

将节点功率平衡方程f、变流器约束方程hse和hsh简记为：

f(Vsys,Vse,Vsh)=0

(10)

hse(Vsys,Vse,Vsh)=0

(11)

hsh(Vsys,Vse,Vsh)=0

(12)

其中，下标sys表示系统;Vsys包括非平衡节点电压相角和PQ节点电压幅值。将式(10)—(12)线性化：

(13)

其中，J为雅可比矩阵。

潮流可调范围是受串联变流器电压Vse控制的，为了量化ΔVse对Δhse的影响，消去变量ΔVsys和ΔVsh。由于负荷和发电机的响应比UPFC的控制动作慢，且串并联变流器与系统交换无功相互独立，因此令Δf=Δhsh=0，由式(13)解出：

(14)

(15)

其中，∂Vsys/∂Vse、∂Vsh/∂Vse分别为节点电压、并联电压对串联电压的灵敏度矩阵，分别如式(16)、(17)所示。

(16)

(17)

将式(14)、(15)代入式(13)，可得潮流控制范围Δhse与串联电压可调范围ΔVse的线性关系为：

(18)

其中，M为灵敏度矩阵。

令受控线路有功设定值为Pref，无功设定值为Qref，此时串联电压幅值为Vse，相角为θse。UPFC潮流调节能力强，Vse在较小范围内变化即可达到控制目标，因此串联变流器潮流控制目标线性可调范围为：

Δhse,min=M[θse-θse,minVse-Vse,min]T

(19)

Δhse,max=M[θse,max-θseVse,max-Vse]T

(20)

3 算例分析

3.1 两阶段潮流算法的验证

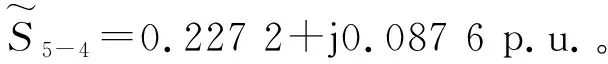
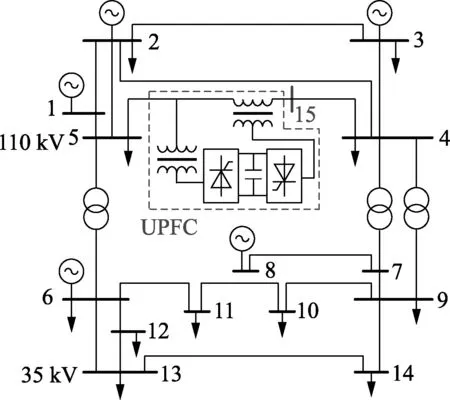
图4 加装UPFC的IEEE 14节点系统Fig.4 IEEE 14-bus system with UPFC

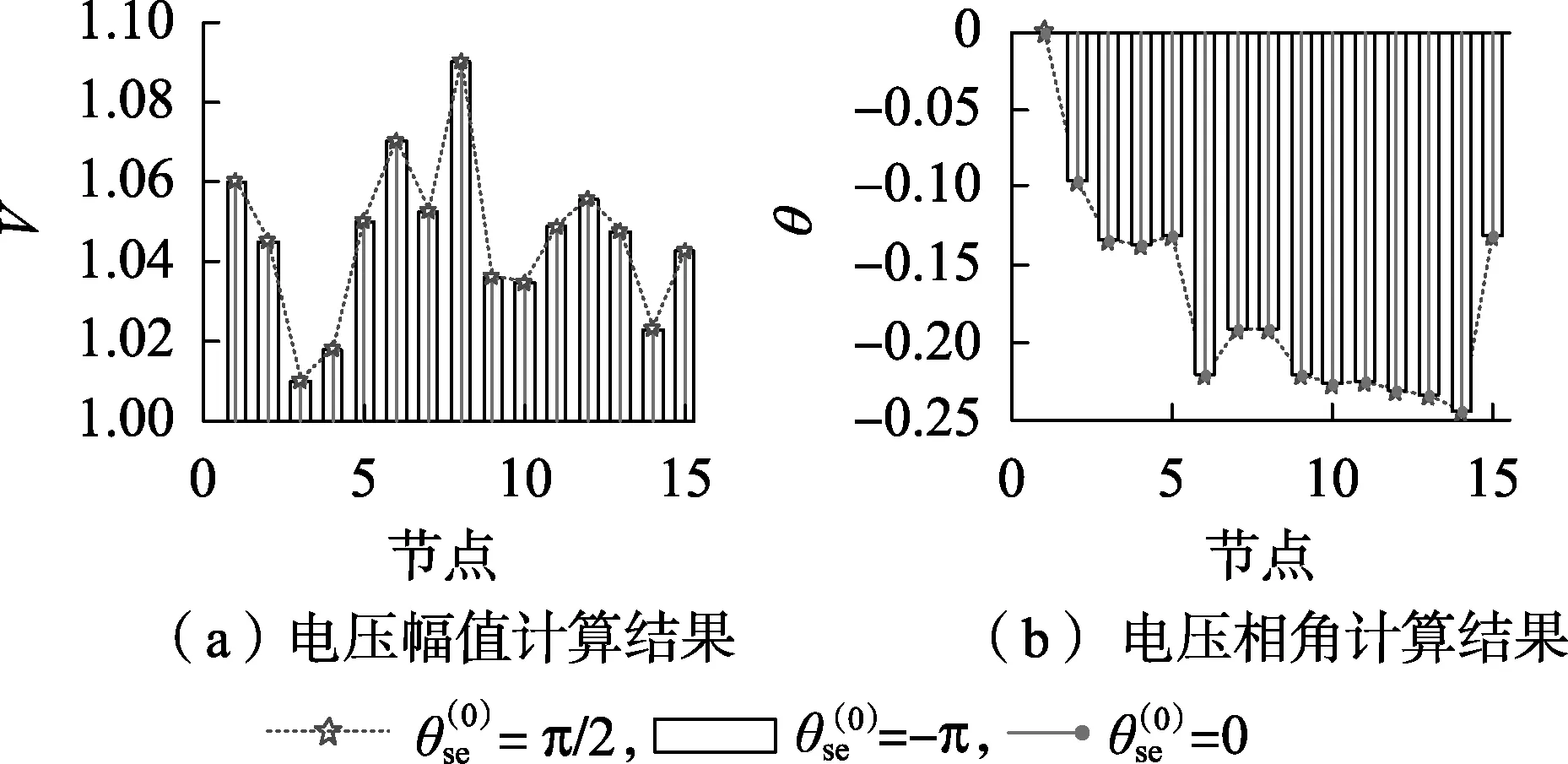
图5 不同对节点电压影响Fig.5 Impact of different values of on bus voltages

表2 不同下UPFC参数Table 2 UPFC parameters with different values of

取收敛精度δ=10-8p.u.，表3给出在不同潮流控制目标下，采用常规潮流和本文两阶段潮流算法的串联电压、迭代次数和计算时间(表中电压、功率均为标幺值)。常规潮流所得电压幅值小于0时，相角与正确解间相差π；电压幅值大于0时，若对应相角超出[-π，π]范围，其值与正确解之间相差2π。而两阶段潮流算法电压幅值均大于0，相角在[-π，π]范围内，显然更加合理。

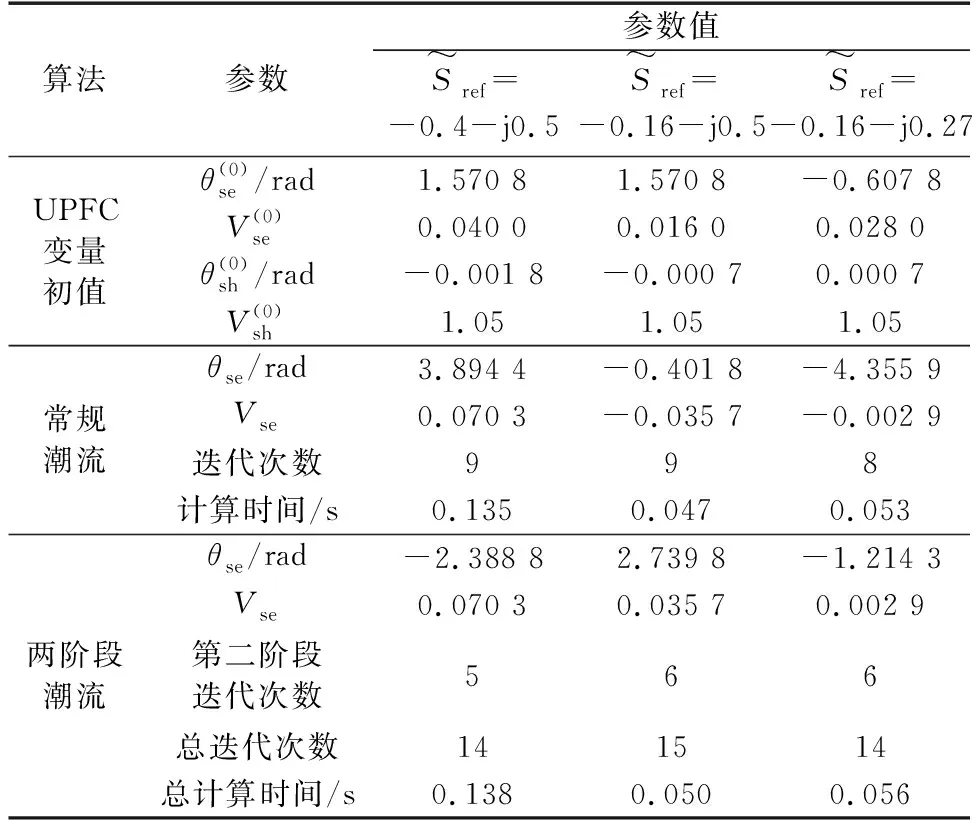
表3 两阶段潮流与常规潮流结果对比Table 3 Results comparison between two-stage power flow and conventional power flow

取Qref=-0.5 p.u.，Pref变化时，由传统方法估算的相角初值却保持1.570 8 rad不变，初值估算误差较大，导致9次迭代后收敛。对比之下，两阶段潮流算法的迭代次数更多，是2次潮流计算导致的。但第二阶段经过5～6次迭代即可收敛，表明经过对相角初值估算，潮流收敛速度得到改善。

相比常规潮流，两阶段潮流算法多了估算相角和第二阶段潮流计算，总计算时间仅增加几毫秒，不影响两阶段潮流算法的计算效率，但计算结果更加准确，对UPFC不同控制目标的适用性更好。

3.2 UPFC潮流控制范围的比较

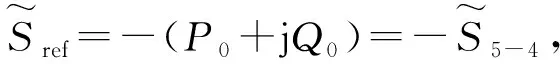
图6 不同方法下潮流控制范围对比Fig.6 Comparison of power flow controllable ranges among different methods

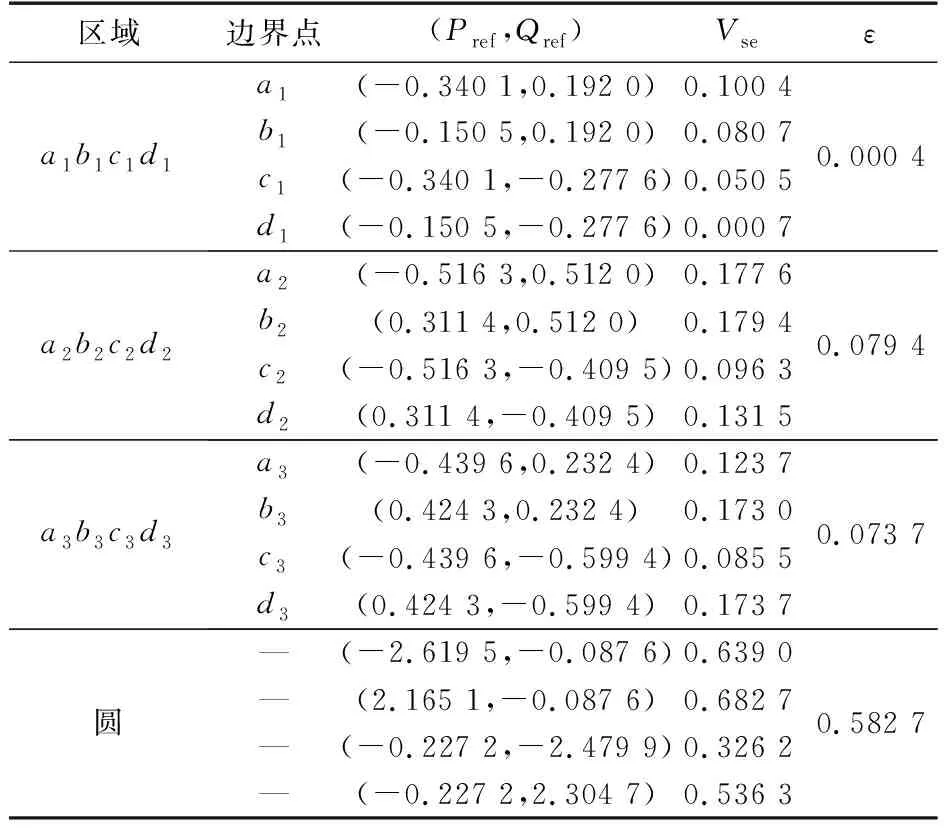
区域边界点(Pref,Qref)Vseεa1b1c1d1a1(-0.340 1,0.192 0)0.100 4b1(-0.150 5,0.192 0)0.080 7c1(-0.340 1,-0.277 6)0.050 5d1(-0.150 5,-0.277 6)0.000 70.000 4a2b2c2d2a2(-0.516 3,0.512 0)0.177 6b2(0.311 4,0.512 0)0.179 4c2(-0.516 3,-0.409 5)0.096 3d2(0.311 4,-0.409 5)0.131 50.079 4a3b3c3d3a3(-0.439 6,0.232 4)0.123 7b3(0.424 3,0.232 4)0.173 0c3(-0.439 6,-0.599 4)0.085 5d3(0.424 3,-0.599 4)0.173 70.073 7圆—(-2.619 5,-0.087 6)0.639 0—(2.165 1,-0.087 6)0.682 7—(-0.227 2,-2.479 9)0.326 2—(-0.227 2,2.304 7)0.536 30.582 7

注：ε表示各个区域边界点求出的串联电压最大值超出Vse,max的量。

由图6和表4可看出，现有方法比灵敏度模型所求出的控制范围大，且圆形控制范围边界点Vse远超最大电压，原因在于现有方法忽略了UPFC加入对节点电压的影响，随着UPFC容量增大，对电网影响越大，现有方法所求控制范围的误差越大，甚至潮流发散，如表5所示(表中数据均为标幺值)。而对于灵敏度模型的控制区域，若仅考虑电压幅值变化，矩形a1b1c1d1误差最小，若考虑相角变化，矩形a2b2c2d2和a3b3c3d3边界点的Vse幅值超出最大值，但误差较小。其原因主要在于截断误差，串联电压相角可在一个圆周内变化，导致线性化潮流控制范围误差稍大，对此问题，可采用分段线性模型求解。

表5 Vse,max=0.2 p.u. 时圆域边界点的串联电压幅值Table 5 Series voltage magnitudes of circle boundary with Vse,max=0.2 p.u.

图7给出了Vse,max=0.1 p.u. 时，潮流控制目标在矩形a1b1c1d1内变化串联电压幅值(图中横轴、纵轴均为标幺值)。从三者关系Pref-Vse和Qref-Vse可看出，可行域内任意潮流控制目标值对应的Vse均没有超过0.1 p.u.，从而证明了基于灵敏度模型所量化的潮流控制范围能保证潮流结果不超出串联电压约束。考虑到UPFC串联变流器可在圆周内任意调整电压相位，应用灵敏度模型时，可只考虑幅值变化对潮流控制范围的影响。

图7 潮流设定值在a1b1c1d1内对应的VseFig.7 Vse correspongding to power setting in area a1b1c1d1

4 结论

本文针对含UPFC电网，提出基于初值预估计的两阶段潮流算法，改善潮流收敛性；建立灵敏度模型，量化UPFC潮流控制范围，得到如下结论。

a. 在潮流控制目标一定的情况下，UPFC串联电压相角初值的选取仅影响串联电压，不影响节点电压和并联电压。

b. 当潮流得到的串联电压幅值为正数时，对应的串联电压相角与正确解相差π的偶数倍；当电压幅值为负数时，对应电压相角与其解相差π的奇数倍。基于此现象估算串联电压相角，将估算结果作为潮流初值，避免了潮流收敛性对变流器电压初值的依赖。

c. 采用灵敏度模型得到的潮流控制范围比圆域的误差要小，其中只考虑串联电压幅值变化的误差最小。由于UPFC变流器串联电压相位可在圆周内任意调整，潮流调节能力强，故灵敏度模型线性化潮流控制范围时只考虑串联电压幅值的变化，即可保证线性化区域内潮流设定值的潮流结果不超过串联变流器电压约束范围。