Magnetic Properties of XXZ Heisenberg Antiferromagnetic and Ferrimagnetic Nanotubes∗
2018-12-13ZhengNanXianYu鲜于正楠andAnDu杜安
Zheng-Nan XianYu(鲜于正楠)and An Du(杜安)
College of Sciences,Northeastern University,Shenyang 110819,China
AbstractThe spin-1/2 antiferromagnetic and spin-(1/2,1)ferrimagnetic single-walled nanotubes are described by XXZ Heisenberg model.The sublattice magnetization and the critical temperature of the system are calculated by using the double-time spin Green’s function method.At zero temperature,with the increase of the exchange interaction in the circumferential direction,a maximum value appears in the sublattice magnetization curves of antiferromagnetic and ferrimagnetic systems.As the diameter of the tube increases,the spin quantum fluctuations and thermal fluctuations are suppressed.In addition,the spin quantum fluctuation of the spin-1/2 antiferromagnetic system is greater than that of the spin-(1/2,1)ferrimagnetic system.The critical temperature of the system increases firstly and then tends to a constant with the increase of the diameter of tube,and it decreases to zero as the exchange anisotropy of the system disappears.
Key words:nanotube,XXZ Heisenberg model,quantum fluctuation,thermal fluctuation,critical temperature
1 Introduction
In recent years,magnetic nanomaterials have become a hotspot in experimental and theoretical research due to their outstanding contributions in magnetic recording,high-density data storage and sensors.[1−3]Since the single-walled carbon nanotube was discovered,[4]nanotubes as a kind of hollow tubular nanomaterial have exhibited many different characteristics from solid nanomaterials.For example,when used as a high-density storage material,the hollow structure of the nanotubes can effectively avoid the vortex core which appearing in the center vortex of nanowires and nanodisks,and have a more stable vortex state.[5]The head-to-head domain wall of the nanowire does not exist in the nanotube.Experimentally,many magnetic nanotubes have been synthesized,such as Ni,[6]Co,[7]FePt,and Fe3O4[8]nanotubes.
In theoretical research,magnetic nanotubes are mainly described by the Ising model and the Heisenberg model.Under the Ising model,comparing the initial magnetic susceptibility and magnetization,which obtained by the effective field theory,nanowires and nanotubes show many similar magnetic properties.[9−10]The transition temperatures and compensation temperatures of ferrimagnetic nanotubes were found strongly affected by the surface dilution and two compensation points were observed in their phase diagrams.[11]In addition,the free energy was calculated and the first-order phase transition temperature was found.[12]Through Monte Carlo simulations,it was observed that tricyclic loops appear in the hysteresis loop,[13]and there are two distinct peaks in the magnetic susceptibility curve for the core-shell nanotube.[14]The range of existence of compensation temperature for mixed spin core-shell nanotubes under different exchange interactions was given.[15]The Gibbs free energy and magnetization of the mixed spin nanotube system were calculated based on the mean field approximation,and the phase transitions of the metastable and unstable branches of the order parameters were found.[16]Under the Heisenberg model,the ferromagnetic and antiferromagnetic single-walled nanotubes,which containing single anisotropy were studied by using the Green’s function method,the dependence of the initial magnetic susceptibility of ferromagnetic nanotubes on temperature and diameter was given[17]and spin quantum fluctuations were observed in the spontaneous magnetization curves of antiferromagnetic nanotubes.[18]The form of the rolling up(armchair or zigzag)of nanotubes was found strongly in fluence the magnetic properties.[19]
As mentioned above,some magnetic and thermal phenomena of nanotubes have been explained by using the Ising model and the Heisenberg model successfully.However,the nanotubes themselves have spatial anisotropy and seem to also have anisotropy in the exchange interaction between spins.So,it is more reasonable to use anisotropic Heisenberg model(XXZ model)to describe magnetic nanotubes.Several works have been done to explore the magnetic properties of nanotubes using the XXZ model.For example,the quantum phase transitions of a three-leg frustrated spin nanotube was studied by using a numerical diagonalization method,[20]and a new quantum phase transition between the 1/3 magnetized plateau and the non-magnetized plateau was found.The critical temperature dependence of the exchange anisotropy was investigated by the effective field theory.[21]Besides,some theoretical interests have also been focused on the mixed spins ferrimagnetic nanomaterials,[22−24]such as Ising nanowire[22]with mixed spins-(1/2,1),Ising nanotubes[23−24]with mixed spins-(1,3/2)and mixed spins-(2,3/2),etc. Compared with the antiferromagnetic system,ferrimagnetic system can exhibit some more abundant magnetization and critical behaviors.Therefore,in this paper,using the Green’s function method,we calculate the zero-temperature magnetization,spontaneous magnetization and the critical temperature of the antiferromagnetic-1/2 and ferrimagnetic-(1/2,1)nanotubes described by the XXZ model,discuss the effect of the exchange anisotropy,diameter of the tube to the sublattice magnetizations and the critical temperature of the system.The article is arranged as follows.In Sec.2,we present the model and formulation.In Sec.3,the numerical results and discussions are presented.Finally,we summarize our main conclusions.
2 Model and Method
We consider a magnetic single-walled nanotube with antiferromagnetic exchange interaction between each two spins,as depicted in Fig.1.

Fig.1 (Color online)Schematic representation of the antiferromagnetic nanotube.
The Hamiltonian of the system is given by
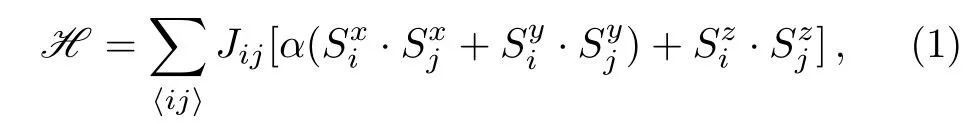
the index 〈ij〉denotes the summation of pair of nearestneighbor spins,Jijand α denote the nearest-neighbor exchange interaction and the exchange anisotropy between the spin Siand Sj.Jij=Jswhen both spins are in circumference direction.Jij=Jlwhen both spins are along the axis of nanotube.For α=0 and 1,the system becomes the Ising models and isotropic Heisenberg models,respectively.
In order to investigate the magnetic properties of the system,we divide the lattice into two interpenetrating sublattice A and B,denoted by red and yellow dots(arrows)in Fig.1.Introducing the retarded Green’s function according to Callen[25]

where Bj=,u is a Callen’s parameter.[25]Using equation motion for Green’s functions
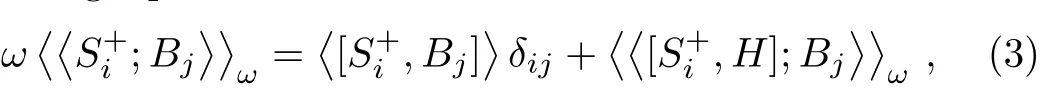
and decoupling the higher order Green’s function on the right hand side of the equations with random phase approximation(RPA),[26−28]

When α=0,RPA is similar to the mean field approximation,the resulting transition temperature of the 2D Ising square lattice(m→∞)could slightly be larger than that of the rigorous calculation.[29−30]When α≠0,this approximation agrees well with other theoretical results.
Because of the spatial symmetry of spins,we can obtain the Fourier component of time transform for Green’s function in Eq.(2).We introduce spatial Fourier transforms[26]of the Green’s function:

where kzis the wave vector along the axial direction within the first Brillouin zone,kc(n)=2πn/ma(n=0,1,2,...,m−1)is the wave vector along the circumferential direction and a is the lattice constant.N is the number of spins in the axial direction,and m is the number of spins along the circumferential direction.For simplicity,here we only take m as an even number.When m is odd number,the frustrated effect of spins in the circumferential direction appears.[20]Then we obtain a group of equations about the Fourier component of the Green’s function:
where p=A,B and p≠p′.By means of the spectral theorem and Callen’s technique,[25]we obtain the expression of sublattice magnetization:
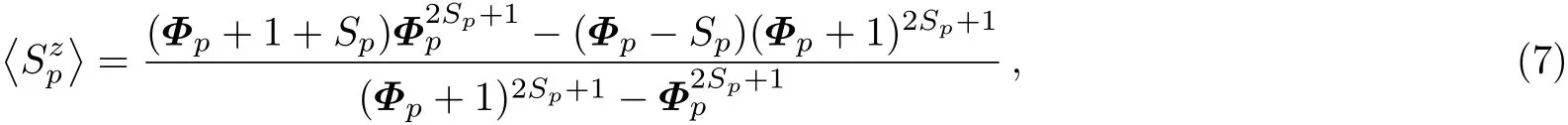
where
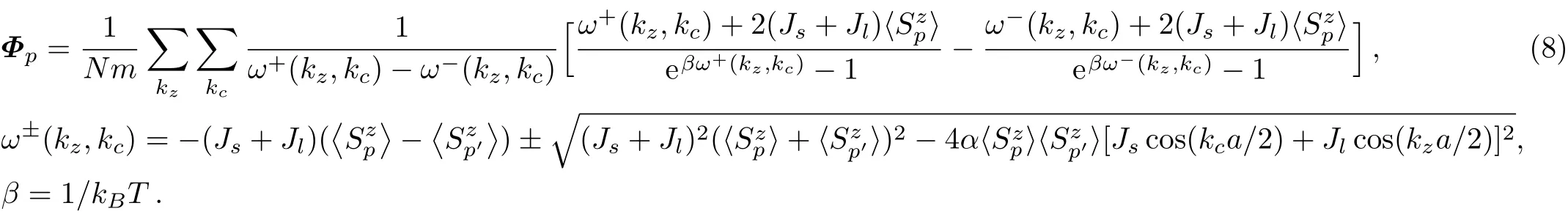
When the temperature is close to critical temperature T→Tc,the sublattice magnetization tends to zero,and Φ approaches in finity.Equation(7)could be approximated as

Because ω(kz,kc)is proportional to 〈Sz〉,taking eω/kBTc− 1 ≈ ω/kBTc,then the critical temperature is given approximately by

When calculating the critical temperature,we must getsimultaneously.The specific expression of the critical temperature can refer to the previous study on the layered Heisenberg ferrimagnets.[31]
In calculation,all parameters are taken as dimensionless quantities.We take|Jl|as the unit of energy,all the exchange interactions and temperature are reduced by|Jl|=1.0.For the sake of brevity,we also take}=1.0 and kB=1.0.
3 Numerical Results and Discussion
Using the above equations,we study magnetization and critical temperature of spin-1/2 antiferromagnetic and spin-(1/2,1)ferrimagnetic nanotubes by adjusting the exchange interaction,diameter and exchange anisotropy.
3.1 Zero-Temperature Magnetization
In this subsection,we focus on the effects of exchange interaction strength in circumferential direction and diameter of nanotube on the magnetization at zero temperature.The sublattice magnetization can be obtained based on Eqs.(7),(8),and the numerical results are shown in Figs.2–3.In order to show the variation of the quantum fluctuations with the exchange interaction and the diameter of nanotubes more clearly,we take the exchange anisotropy α=0.8.

Fig.2(Color online)The sublattice magnetization as a function of the antiferromagnetic exchange interaction Jsat zero temperature with m=6,α=0.8.(a)spin-1/2 antiferromagnetic nanotube(b)spin-1/2 and 1 ferrimagnetic nanotube.
In Fig.2,we can see that the sublattice magnetizations are less than their classic values at zero temperature due to the quantum fluctuation effect of spins.As Jsincreases,the sublattice magnetizations increases firstly and then decreases slowly,gets a maximum value near Js=Jl.When Jsis very small,nanotube can be regarded as a number of nearly independent antiferromagnetic spin chains and the quantum fluctuations are large,the long range order is hard to be maintained.When Jsis much larger than Jl,the system can be regard approximately as an in finite number of antiferromagnetic nanorings with a limited number of spins,quantum fluctuation of spins are also bigger,so a maximum of sublattice magnetization appears in Fig.2.Under the same antiferromagnetic exchange interaction and exchange anisotropy,the quantum fluctuation of spin-1/2 antiferromagnetic system is larger than that of spin-(1/2,1)ferrimagnetic system.
Since m is proportional to the diameter of tube(m=πd/a),in the following,we use m as the measure of the diameter of nanotubes.Figure 3 shows the sublattice magnetization change with the diameter of nanotube at zero temperature.It is found that the sublattice magnetization increases monotonically with the increase of the diameter of the tube,and approaches a definite value when the diameter of the tube exceeds 50,indicating the increase of the diameter suppresses the quantum fluctuations of the spins.In addition,in the inset of Fig.3(a),when the anisotropy approaches zero(α=1),the sublattice magnetization of the system equals approximately 0.358,which conforms to the result of 2D spin-1/2 antiferromagnets with square lattice[33−34]and is slightly higher than the result of the spin wave method(0.303)and the method considered the perturbation series(0.313).[32]The quantum fluctuation behaviors of the spin-1/2 and 1 ferrimagnetic system with diameter of the tube(Fig.3(b))are similar to the spin-1/2 antiferromanetic system,but the quantum fluctuations are smaller than that of the antiferromagnetic system for same exchange anisotropy.
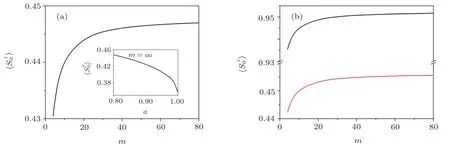
Fig.3 (Color online)The sublattice magnetization as a function of parameter m at zero temperature with Js=1.0,α=0.8.(a)spin-1/2 antiferromagnetic nanotube(b)spin-1/2 and 1 ferrimagnetic nanotube.
3.2 Spontaneous Magnetization
Figure 4 shows the temperature dependence of the sublattice magnetization with some diameters of nanotube.We can see that the sublattice magnetizations decrease with the increase of temperature,but increasing of the diameter of nanotube,the sublattice magnetization increases,indicating the increase of the diameter of nanotube suppresses the thermal fluctuation of the spins.Besides,when the diameter of nanotubes exceeds 20,the difference of spontaneous magnetizations is getting smaller and smaller.
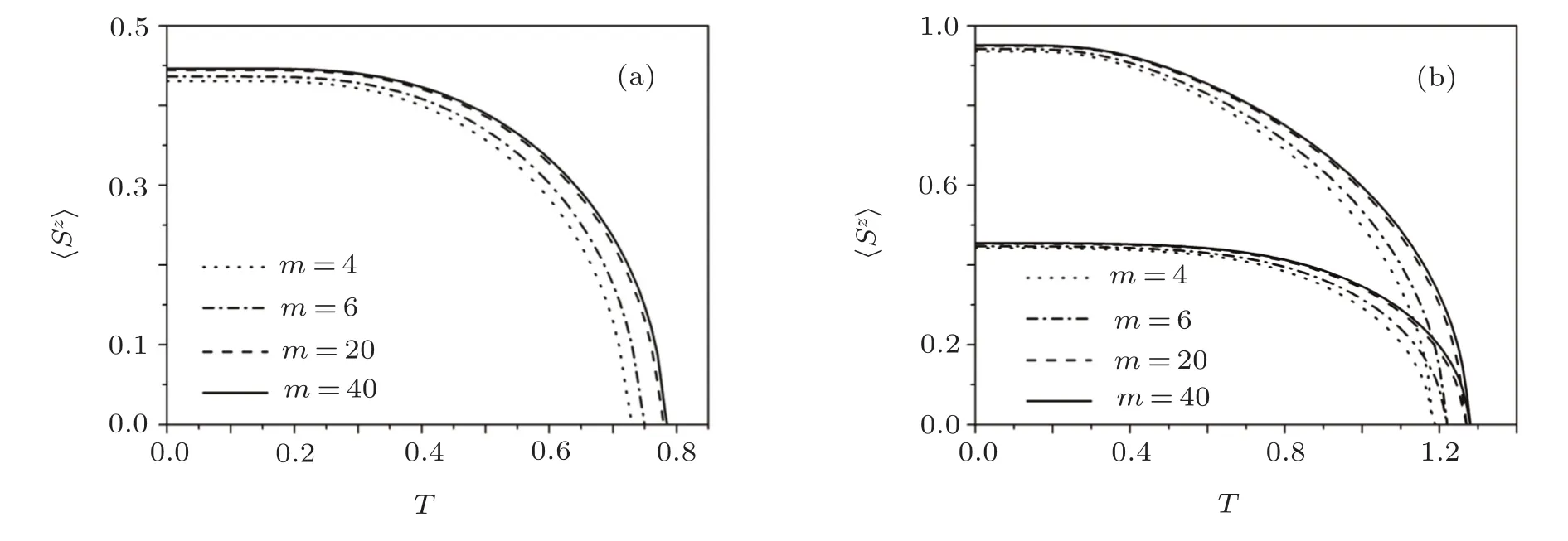
Fig.4 The sublattice magnetization as a function of parameter m at zero temperature with Js=1.0,α=0.8.(a)spin-1/2 antiferromagnetic nanotube(b)spin-1/2 and 1 ferrimagnetic nanotube.
3.3 Critical Temperature
The critical temperature of system can be obtained based on Eqs.(9)and(10).We mainly discuss the effect of nanotube diameter and exchange anisotropy on the critical temperature of the system.
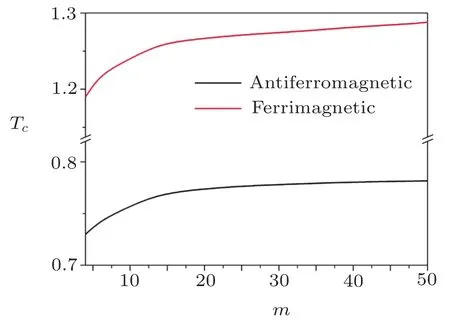
Fig.5(Color online)The critical temperature as a function of diameter for spin-1/2 antiferromagnetic and spin-1/2 and 1 ferrimagnetic nanotubes with α=0.8.
In Fig.5,as the nanotube diameter increases,the critical temperature first increases and then tends to constant,and this is also re flected in Fig.4.When m is small,the system which with small exchange anisotropy is difficult to keep magnetic order,the critical temperature is low.As the diameter increases,the system changes from one-dimensional to two-dimensional system gradually,and the critical temperature of the system tends to be stable.In the above discussion,we have made the exchange anisotropy of the system very small for the sake of clarity.Figure 6 shows the changes in the critical temperature of the system when the system is transformed from the Ising model to the Heisenberg model.When the anisotropy parameter is equal to 0,the Hamiltonian becomes Ising model and its critical temperature has been discussed deeply.[35−36]
As the anisotropy parameter increases,the critical temperature decreases and when the anisotropy parameter approaches 1,the critical temperature drops to zero,this is conform to the Mermin and Wagner’s theory,[37]but different from the results of double-walled nanotube,[21]when the exchange anisotropy disappears,its critical temperature is not equal to zero.In addition,the effect of exchange anisotropy on the critical temperature of the ferrimagnetic system is greater than that of the antiferromagnetic system when α is close to 1.

Fig.6 (Color online)The critical temperature Tcas a function of exchange anisotropy parameter α for spin-1/2 antiferromagnetic and spin-1/2 and 1 ferrimagnetic nanotubes with m=6.
4 Summary
In this work,we have studied the magnetization and critical temperature of the spin-1/2 antiferromagnetic and spin-(1/2,1)ferrimagnetic single-walled nanotubes,which are described by the XXZ model.At zero temperature,with the increase of the exchange interaction in the circumferential direction,a maximum value appears in the sublattice magnetization curves of antiferromagnetic and ferrimagnetic systems near the point where the exchange interaction in circumferential and the axial directions are equal.With the increase of the diameter of nanotubes,both spin quantum fluctuations and thermal fluctuations are suppressed.Besides,the spin quantum fluctuations of the spin-1/2 antiferromagnetic system are larger than that of the spin-(1/2,1)ferrimagnetic system.As the diameter of nanotubes increases,the system changes from one-dimensional to two-dimensional systems and the variation of the critical temperature of the system is getting smaller and smaller.When the anisotropy parameter increases from 0 to 1,the system transforms from the Ising model to the Heisenberg model,and the critical temperature of the system reduces to zero.
杂志排行
Communications in Theoretical Physics的其它文章
- Electron Transport Properties of Graphene-Based Quantum Wires∗
- On the Singular Effects in the Relativistic Landau Levels in Graphene with a Disclination∗
- Super-sensitivity in Dynamics of Ising Model with Transverse Field:From Perspective of Franck-Condon Principle∗
- New Feedback Control Model in the Lattice Hydrodynamic Model Considering the Historic Optimal Velocity Di ff erence Effect∗
- A Class of Rumor Spreading Models with Population Dynamics∗
- Directed Dominating Set Problem Studied by Cavity Method:Warning Propagation and Population Dynamics∗
