On the Singular Effects in the Relativistic Landau Levels in Graphene with a Disclination∗

Rosinildo F.do Nascimento, Diego Cogollo, Edilberto O.Silva, Moisés Rojas,and Cleverson Filgueiras,¶

1Instituto de Física,Universidade Federal de Uberlândia,Uberlândia,MG,Brasil

2Unidade Acadêmica de Física,Universidade Federal de Campina Grande,POB 10071,58109-970,Campina Grande-PB,Brazil

3Departamento de Física,Universidade Federal do Maranhão,65085-580,São Luís-MA,Brazil

4Departamento de Física,Universidade Federal de Lavras,Caixa Postal 3037,37200-000,Lavras-MG,Brazil

AbstractThe effect of a pseudo Aharonov-Bohm(AB)magnetic field generated by a disclination on a two-dimensional electron gas in graphene is addressed in the continuum limit within the geometric approach.The in fluence of the coupling between the spinor fields and the singular conical curvature is investigated,which shows that singularities have pronounced impact in the Hall conductivity.Moreover,the degeneracy related to the Dirac valleys is broken for negative values of the angular momentum quantum numbers,ℓ,including ℓ≡ 0.In this case,a Hall plateau develops at the null filling factor.Obtaining the Hall conductivity by summing over the positive and the negative ℓ′s,the null Landau level is recovered and the plateau at the null filling factor disappears.In any case,the standard plateaus,which are seen in a lf at graphene are not obtained with these curvature and singular effects.

Key words:Landau Levels,Hall conductivity,Graphene,Elastic deformations

1 Introduction

The carriers within Graphene behave as twodimensional massless Dirac fermions.[1−4]Its peculiar physical properties make it promising for nanoelectronic applications.[5−8]Graphene can be viewed as a zero-gap semiconductor,which in turns puts an obstacle towards the engineering of electronic devices based on it.It is worth to mention that there are possibilities to induce a gap by applying a perpendicular DC[9−10]and AC fields.[11−12]Another alternative to open a gap consists in inducing a strain field in a graphene sheet onto appropriate substrates.[13]In the continuum,these strain fields appear as effective gauge fields which yields pseudo magnetic fields.[14]One important difference from the actual magnetic fields is that they do not violate the time reversal symmetry.[15]A numerical study on the uniformity of the pseudomagnetic field in graphene as the relative orientation between the graphene lattice and straining directions was carried out in Ref.[16]and it was pointed out that observing them in Raman spectroscopy setup is feasible.In Ref.[17],two different mechanisms that could underlie nanometer-scale strain variations in graphene as a function of externally applied tensile strain is presented.A device to detect micro stresses in graphene able to measure AB interference at the nanometer scale was proposed in Ref.[18].It was shown on it that fictitious magnetic field associated with elastic deformations of the sample yields interference in the local density of states.A pseudo AB- field can also be induced by a topological defect called disclination.[19]The physical properties of graphene can be affected by topological defects in significant ways.Extensive studies on this manner have been carried out over the last years,[20−23]etc.Topological Defects could be viewed,at first,as imperfections which could affect the graphene performance. Therefore,research on defects and how they may in fluence the dynamics of carriers in graphene is important for the improvement of its technological applications.[24]This kind of defect appears as a result of removing(inserting)one or several carbon atoms from(into)the honeycomb lattice,not affecting the threefold coordination of other atoms,which leads to the warping of the graphene sheet. As a consequence,a positive(negative)curvature is induced at the location of a defect.Although the literature of topological defects in graphene is so vast,some important effects of them in its electronic properties still must be clarified.For example,the graphene sheet with a disclination takes shape of a cone with the value of the apex angle related to the num-ber of removed atoms.In the continuum approach,the geometric model for the elastic deformations introduced by topological defects in elastic solids is employed.[25]In this approach,the defects are represented by metrics with proper boundary conditions associated with them.So,the impact of the topology of a disclination together with the in fluence of a singular curvature represented by the Ricci scalar in the continuum limit are important aspects to be addressed.Assuming that the size of a defect is small as compared to the whole size of the graphene sample,we will investigate the in fluence of such a disclination on the relativistic Landau levels and,as consequence,in the Hall conductivity in a suspended graphene.It is important to point out that the problem addressed here can not be viewed as a clean non-interacting 2D electronic system with one localized impurity under the in fluence of a constant magnetic field.In such case,the Quantum Hall Effect(QHE)can not be modified,because this one impurity will produce one state between Landau levels that will not be visible in experiments.[26]However,a sample with such a elastic deformation caused by a disclination induces an extra gauge field,as discussed in Ref.[18].In this case,modifications in the QHE are going to be observed.

The existence of a singular curvature make us to consider the existence of both the regular and the irregular wavefunctions as solutions of the problem.This fact depends either on the existence or not of the coupling between the spinor fields and the Ricci scalar(a deltalike curvature on a cone).So,the correct behavior of wavefuntions whenever we have singularities is investigated here,like in other quantum systems found in the literature.[27−31]Actually,conical singularities have significant impact in the QHE.[32]In our case,we will show that,if singular effects do not manifest,then a constraint in the orbital angular momentum eigenvalues shows up.The coupling of the wave functions with the delta-like curvature of the cone introduces the zero value of the angular momentum in the energy spectrum.This fact significantly in fluences the Hall conductivity.By considering the system prepared with only negative values of the angular momentum,the zero-energy,which exist when just a constant orthogonal magnetic field is present,does not develop around Dirac valleys,represented by K and K′.Then,a Hall plateau develop at the null filling factor(dimensionless ratio between the number of charge carries and the flux quanta).On the other hand,analyzing the QHE summing over all the orbital angular momentum eigenvalues allowed for the system(positive and negative),it is observed the standard plateaus at all integer n of 2e2/h,including n=0.This is due to the degeneracy related to the Dirac valleys,which is broken for negative values of the angular momentum.This contrasts with the usual QHE in graphene:for it,the quantum Hall conductivity exhibits the standard plateaus at all integer n of 4e2/h,for n=1,2,3,...,and 2e2/h for n=0.

The plan of this work is the following.First,we briefly discuss the disclination in the context of the geometric approach.Next,we investigate how a pseudo AB field introduced by a disclination on a graphene sheet is going to affect the relativistic Landau levels.Then,we investigate the in fluence of it in the quantized Hall conductivity.At the end,we have the concluding remarks.

2 A Disclination in the Geometric Approach

In the Volterra process,a disclination is a topological defect associated to the removal of a wedge of threedimensional material with the subsequent identification of the loose ends.It introduces an angular deficit,which changes the boundary condition on the angular variable:ϕ → ϕ+2π becomes ϕ → ϕ+2πα.[25]The case α <1 holds for the removed wedge angle of 2π(1−α).Conversely,if a wedge is added,α>1.This new boundary condition can be applied by working in a background space with the line element

As it was shown in Ref.[25],the Frank vector which characterizes a disclination is the curvature flux associated to the defect.The above line element corresponds to a curvature scalar given by R=2((1 − α)/α)(δ(ρ)/ρ)and its flux is I

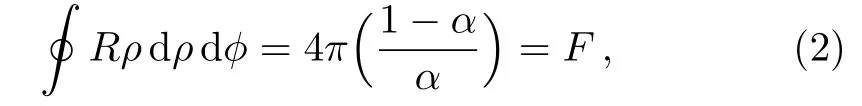
giving the Frank vector F(topological charge of the disclination).This result still holds for a two-dimensional surface with a disclination,which is a graphene sheet with a conical shape.This is the subject of this article.For graphene,α =1± λ/2π.In fact,to respect the symmetries of the carbon network,we must have λ = ±jπ/3,where j is an integer in the interval(0,6).[33]For j≡1,α =1 − λ/2π =5/6(α =1+ λ/2π =7/6)stands for a graphene sheet where a single hexagon was substitute by a one-pentagon(one-heptagon)apex,creating a cone like(saddle-like)structure.In the continuum,both of them can be described by the metric(1).We consider only these two cases in what follows.

3 Relativistic Landau Levels Around a Disclination

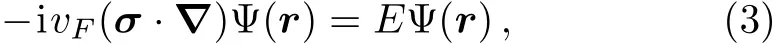
In this section,we will investigate how a disclination on a graphene sheet is going to affect the relativistic Landau levels.The low energy excitation of graphene behave as massless Dirac fermions.[3,34]Their internal degrees of freedom are:sublattice index(pseudospin),valley index( flavor),and real spin,each one taking two values.The real spin will not be taken into account since it is irrelevant in our problem.Then,the low energy excitation around a valley is described by the(2+1)-dimensional Dirac equation as follows where σ =(σx,σy)are the Pauli matrices,Ψ =(φ1,φ2)Tis a two component spinor field,the speed of light c was replaced by the Fermi velocity(vF≈106m/s)andhas been fixed equal to one.The electronic states around the zero energy belong to the distinct sublattices,which is the reason of the existence of a two component wavefunction.Two indexes to indicate these sublattices,similar to spin indexes(up and down),must be considered.The inequivalent corners of the Brillouin zone,which are called Dirac points,are labeled as K and K′(valley index).[14]

In this work,both the curvature and the topology of a graphene due to a disclination introduce two extra fields into the system:A1+A2,where A1is due to the correction introduced by the conical geometry of graphene and A2is due to the existence of a non-abelian gauge field,a term which breaks the degeneracy of the energy levels around the valleys.[14]This means that different signals must be considered for this gauge field at them since it does not break time reversal symmetry.[15]The relativistic Landau levels are achieved by coupling an azimuthal potential vector,given by

from where we get B0=B0z,the constant orthogonal magnetic field.All these vector potentials are inserted into the Dirac equation via a minimal coupling,p→p−eA.The details of such calculations can be found in Ref.[19].They have found that each spinor field satisfy the following differential equation

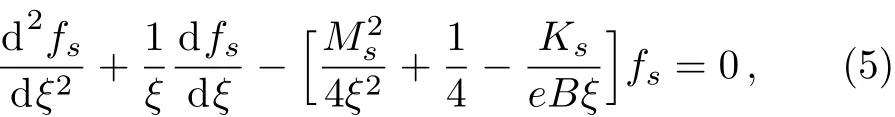
where ξ=eBρ2/2,

The parameter s has a value of twice the spin value,characterizing the two pseudo spin states,with s=+1 for spin “up” and s= −1 for “spin” down.Actually,they correspond to the different sub-lattices in the graphene.

We investigate now some more details regardless the wave solutions as well as the energy spectrum.The general solution to this equation is given in terms of the confluent hypergeometric function of the first kind,[35]

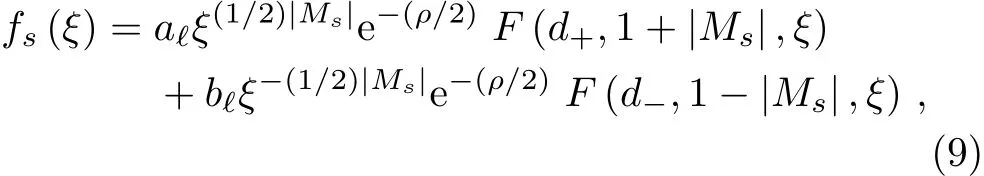
with

where aℓand bℓare,respectively,the coefficients of the regular(non divergent as ξ→ 0)and irregular(divergent as ξ→ 0)solutions. The regular wave solution was investigated in Ref.[19]and it holds for bℓ≡ 0 and|Ms|>1.[30,36]As observed in Ref.[37],the spinor field couples with the Ricci scalar,which is obtained from the singular curvature in our case.So,the irregular solution should also be taken into account,which completes the analysis of the energy spectrum.[38]The two scenarios are possible since it can be introduced a physical mechanism so that the wave solutions become regular at the origin of the coordinate system,recovering the results found in Ref.[19].For aℓ≡ 0,we must have|Ms|<1 for the wave solution to be square integrable.Moreover,fs(r)must vanish at large values of r.So,from the asymptotic representation of the confluent hypergeometric function,this is achieved if

with n being a non negative integer,n=0,1,2,...This way,we obtain

In particular,it should be noted that for the case when|Ms| ≥ 1(the δ interaction is absent),only the regular solutions contribute for the bound state wave function(bℓ≡ 0),and the energy is given by Eq.(12)with plus sign.[19]On the other hand,if a singular interaction is present,then we have to add the energies with the minus signal,for which|Ms|<1.

The energy spectrum above must be analyzed in terms of the values that the α parameter can assume,since the condition|Ms|≥1(|Ms|<1)for the regular(irregular)solution has to be fulfilled.Let us consider the regular wave functions at first.Then,the spectrum(12)in this case can be put in the following way

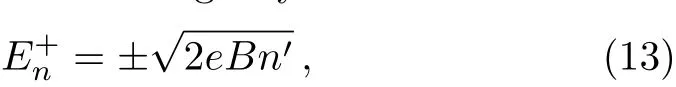
for Ms≥ 1,with n′=n+(1−s)/2=0,1,2,3,...,and

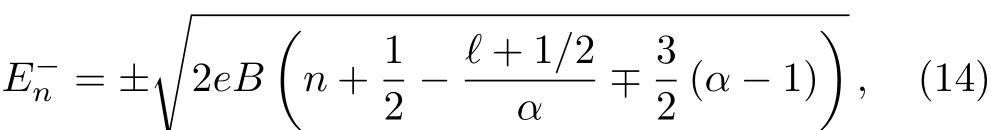
for Ms≤−1,with n=0,1,2,3,...Notice that the degeneracy regardless the sub-lattices,which are represented by the parameter s,is not broken.The degeneracy regardless the Dirac valleys K and K′is not broken in Eq.(13),but it is in Eq.(14).

We now turn our attention to the case considering the irregular solution.We take into account the minus signal in Eq.(12).The energy spectrum is the same as showed in Eqs.(13)and(14),but the constraint|Ms|<1 allows only some values of ℓ,which depends on the values of α.For example,α =5/6(pentagon),we have ℓ= −1,0 only,while that for α=7/6(heptagon),we may haveℓ= −2,−1,0.In contrast,for the regular wave solution,the energies(14)hold for ℓ= −1,−2,−3,...for both cases.The presence of the disclination breaks the degeneracy of the relativistic Landau levels and new levels are introduced in the spectrum only for ℓ=0,−1,−2,−3,...

In summary,in the absence of the coupling between the wavefunctions and the singular curvature,the constraint|Ms|≥1 must be imposed,restricting the allowed momentum eigenvalues ℓ,which guarantees that the wavefunctions are regular as ξ→ 0.If such coupling manifests,then the charge carriers are allowed to have other values of the angular momentum eigenvalues ℓ without such constraint.We will examine these two situations in order to show how singular effects are important if they manifest in the system.

4 The Effect of a Disclination in the Hall Conductivity

In this section,we investigate the in fluence of a disclination in the quantized Hall conductivity.We express the energy scale associated with the magnetic field in the units of temperature as follows,

where vFand B are given in(m/s)and Tesla,respectively.

We start by considering the expression for the Hall conductivity obtained in Ref.[39]in the clean limit.This way,we have

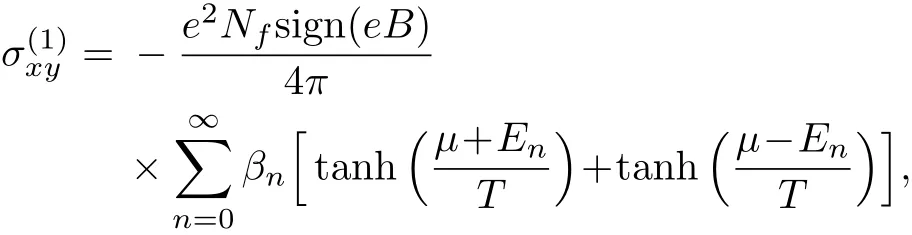
where β0=1(for n=0), βn/β0=2(for n ≥ 1),T is the temperature andµis the chemical potential,which is considered to tune the graphene conductivity.[40]These values are related to the above-mentioned smaller degeneracy of the n=0 Landau level.Here,the degeneracy of energy levels related to these valleys is broken due to the disclination when ℓ=0,−1,−2,−3,...The consequence is that we have to consider a sum in the valley index.Therefore,we have the Hall conductivity as

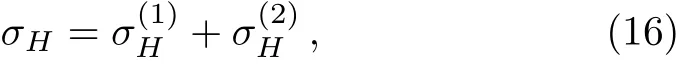
with

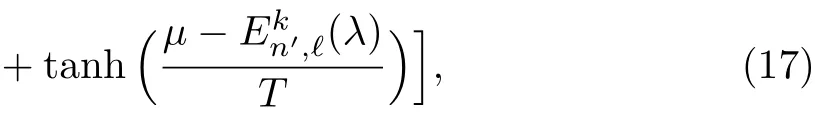
where βn′,ℓ(λ)=1,for any n′and ℓ.

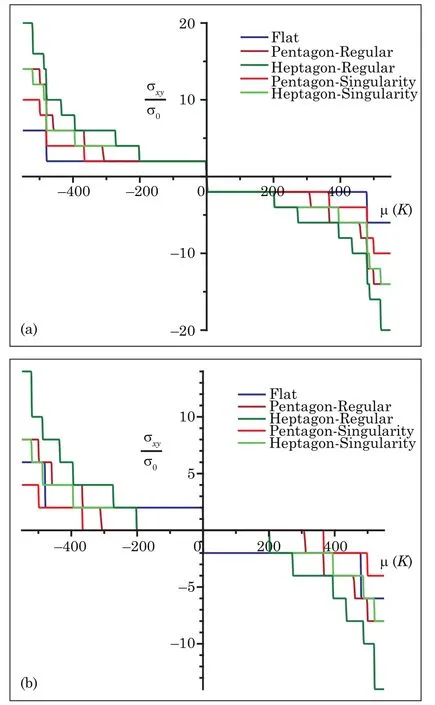
Fig.1 (Color online)Hall conductivity versus the chemical potential for α=5/6(one-pentagon apex)and α=7/6(one-heptagon apex). In(a),we haveℓ=0,±1,±2,...while in(b)we have ℓ=0,−1,−2,...and a plateau develops at σxy=0.

In Fig.1,we plot the Hall conductivity versus the chemical potential for different values of α.In the Quantum Hall effect in flat graphene(α≡1),the quantum Hall conductivity exhibits the standard plateaus at all integer n of 4e2/h,for n=1,2,3,...,and 2e2/h for n=0. For α≠1,intermediate plateaus are introduced between them.In Fig.1(a),the plot is built forℓ=0,±1,±2,±3,...and the quantum Hall conductivity exhibits the standard plateaus at all integer n of 2e2/h.In Fig.1(b)we analyze the case supposing that the system is prepared so that only the energies containing the parameter α are possible to be occupied by the charge carriers,that is,ℓ=0,−1,−2,−3,...In this case,we have the condition Ms>1(regular solutions)and−1

For α<1,the plateaus widths decrease and they decrease even more when α>1.For positive(negative)values of the chemical potentialµ,the steps shift to lower(higher)values of it.Nevertheless,due to the splitting of energy levels caused by the disclination,the number of states under the Fermi level increases,raising(lowering)the Hall conductivity forµ <0(µ >0)with respect to the flat sample case.The coupling of the wavefunctions with the curvature at the cone apex make these effects less pronounced,modifying the Hall conductivity in a significant way.

5 Concluding Remarks

In this work,we investigated how both the relativistic Landau levels and the quantum Hall conductivity are modified if fermions on graphene are held in the presence of a constant orthogonal magnetic field along with a pseudo AB- field induced by a disclination.We considered the continuum limit within the geometric approach.The squared Dirac equation yielded a differential equation whose solutions are well established in terms of Hypergeometric series,which contains both regular and irregular functions.We have observed that,for the existence of constraints on the orbital angular momentum eigenvalues allowed for the system(Ms≥1 for regular wavefunctions and−1

As a final word,we have shown how a conical singularity can affect the relativistic Landau levels in graphene.It is important to have those questions in mind if one is interested to probe the effects of a singular curvature in these systems.The results found here may shade some light also in other graphene like materials with disclinations.