Existence and Dynamics of Bounded Traveling Wave Solutions to Getmanou Equation∗

Zhen-Shu Wen(温振庶)

School of Mathematical Sciences,Huaqiao University,Quanzhou 362021,China

AbstractIn this paper,we study the existence and dynamics of bounded traveling wave solutions to Getmanou equations by using the qualitative theory of differential equations and the bifurcation method of dynamical systems.We show that the corresponding traveling wave system is a singular planar dynamical system with two singular straight lines,and obtain the bifurcations of phase portraits of the system under different parameters conditions.Through phase portraits,we show the existence and dynamics of several types of bounded traveling wave solutions including solitary wave solutions,periodic wave solutions,compactons,kink-like and antikink-like wave solutions.Moreover,the expressions of solitary wave solutions are given.Additionally,we confirm abundant dynamical behaviors of the traveling wave s olutions to the equation,which are summarized as follows:i)We confirm that two types of orbits give rise to solitary wave solutions,that is,the homoclinic orbit passing the singular point,and the composed homoclinic orbit which is comprised of two heteroclinic orbits and tangent to the singular line at the singular point of associated system.ii)We confirm that two types of orbits correspond to periodic wave solutions,that is,the periodic orbit surrounding a center,and the homoclinic orbit of associated system,which is tangent to the singular line at the singular point of associated system.

Key words:getmanou equation,bounded traveling wave solutions,existence,bifurcations,dynamics

1 Introduction

Nonlinear wave phenomena exist in all fields including either the scientific work or engineering fields,such as fluid mechanics,plasma physics,optical fibers,biology,solid-state physics,chemical kinematics,and chemical physics.Studying traveling wave solutions of nonlinear wave equations is playing important roles in the analysis of these phenomena.[1−2]Many methods have been employed to find exact traveling wave solutions of nonlinear wave equations,such as F-expansion method,[3](G′/G)-expansion method,[4]Bäcklund transformation method[5]and so on.In this paper,we will study the existence and dynamics of bounded traveling wave solutions to the Getmanou equation

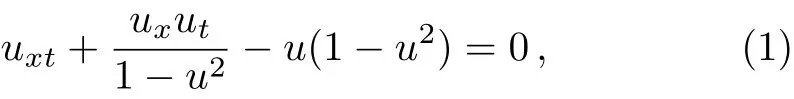
from the perspective ofthe theory ofdynamical systems.[6−15]Equation(1)possesses high nonlinearity and has been little studied.Reference[16]studied the single traveling wave solutions based on the complete discrimination system of the fifth-order polynomials.Reference[17]further studied the classification of single traveling wave solutions using trial equation method and combing complete discrimination system of fourth-order polynomials.However,it is not so clear that what types of the traveling wave solutions are.Moreover,how about the dynamical behavior of these traveling wave solutions under arbitrary parameters conditions?Driven by this motivation,it is of great necessary to study the existence and dynamics of bounded traveling wave solutions to Eq.(1).In this paper,we not only show the existence of several specific types of bounded traveling wave solutions,but also obtain the expressions of solitary wave solutions.Additionally,we confirm abundant dynamical behaviors of the traveling wave solutions to the equation,such as two types of orbits correspond to solitary wave solutions,and two types of orbits give rise to periodic wave solutions.

2 Bifurcations of Phase Portraits

To study traveling wave solutions to Eq.(1),substituting u(x,t)= φ(ξ)with ξ=x−ct into Eq.(1),it follows,

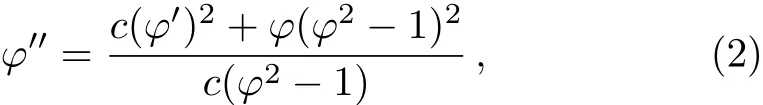
where the prime stands for the derivative with respect to ξ.

From Eq.(2),we obtain the following planar system

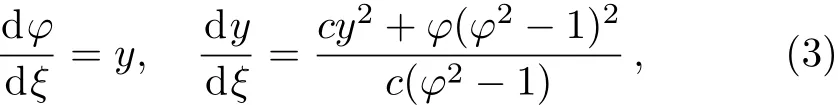
with first integral

Under the transformation dξ=c(φ2− 1)dτ,system(3)becomes a regular system

Since system(3)and system(5)have the same level curves except the singular straight lines l1:φ= −1 and l2:φ=1.Therefore,we should be able to obtain the topological phase portraits of system(3)from those of system(5).

Fig.1 The phase portraits of system(3).(a)c>0,(b)c<0.

Obviously,system(5)has three equilibrium points E0(0,0),E1(−1,0),E2(1,0)on the φ-axis.We can easily know that the equilibrium point E0(0,0)is center when c>0,while it is saddle when c<0.We also learn that the equilibrium points E1(−1,0)and E2(1,0)are high order singular points,the properties of which can be analyzed by the qualitative theory of dynamical systems.

Therefore we obtain the bifurcations of phase portraits of system(3)in Fig.1.

3 Main Results and the Theoretic Derivations of Main Results

To state conveniently,we introduce some marks h0=H(0,0)=0,h1=H(−1,0)= −1/12,h2=H(1,0)=−17/12,where H(φ,y)is given in Eq.(4).

Based on the dynamics of the level curves determined by H(φ,y)=h and the bifurcations of phase portraits of system(3),we state the main results in the following theorems,and the proofs follow.

Theorem 1 When c>0,Eq.(1)has the following four kinds of bounded traveling wave solutions.

(i)When h=h1,there exists a solitary wave solution to Eq.(1),

(ii)When h∈(h1,h0),there exist a family of periodic wave solutions to Eq.(1).

(iii)When h∈(h2,h1)or h∈(−∞,h2),there exist two families of compactons to Eq.(1).

(iv)When h=h2,there exist kink-like and antikinklike wave solutions to Eq.(1).

Proof(i)The homoclinic orbit,defined by H(φ,y)=h1in Fig.1(a),can be expressed as

Substituting Eq.(7)into the first equation of system(3),and integrating along the homoclinic orbit,it follows that

From Eq.(8),we obtain the solitary wave solution(6).

(ii)Corresponding to the family of periodic orbits enclosing the equilibrium point E0(0,0),defined by H(φ,y)=h,h ∈ (h1,h0),Eq.(1)has a family of periodic wave solutions.

(iii)According to the theory of singular nonlinear waves,[2,18−22]corresponding to the family of open orbits passing through the point(φ0,0)with φ0∈ (1/3,1),defined by H(φ,y)=h,h ∈ (h2,h1),Eq.(1)has a family of compactons.As illustration,we simulate the family of compactons in Fig.2(a)by taking c=2.In addition,the family of orbits,which are tangent to the singular straight line l2:φ =1 and defined by H(φ,y)=h,h ∈ (−∞,h2),also give rise to a family of compactons.

(iv)According to the theory of singular nonlinear waves,[2,18−23]corresponding to the stable manifold and unstable manifold on the left of the point E1(1,0),defined by H(φ,y)=h2,Eq.(1)has kink-like and antikink-like wave solutions.Taking c=2,we simulate the kink-like and antikink-like wave solutions in Figs.2(b)and 2(c).

Let F(·,·)be incomplete elliptic integral of the first kind and ∏(·,·,·)be Legendre’s incomplete elliptic integral of the third kind.[24]

Fig.2 The family of compactons,kink-like wave solution,and antikink-like wave solution to Eq.(1)when c=2.(a)The family of compactions;(b)The kink-like wave solution;(c)The antikink-like wave solution.

Theorem 2 When c<0,Eq.(1)has the following four kinds of bounded traveling wave solutions.

(i)When h=h0,there exists a solitary wave solution to Eq.(1),

with

where

(ii)When h∈(h2,h0)or h∈(−∞,h2),there exist two families of periodic wave solutions to Eq.(1).

(iii)When h∈(h1,h0),or h∈(−∞,h1),or h∈(h0,+∞),there exist three families of compactons to Eq.(1).

(iv)When h=h0,there exist kink-like and antikink-like wave solutions to Eq.(1).

Proof(i)The homoclinic orbit,defined by H(φ,y)=h0in Fig.1(b),can be expressed as,

Substituting Eq.(10)into the first equation of system(3),and integrating along the homoclinic orbit,it follows that

We integrate Eq.(11)through elliptic integrals,[24]and obtain solitary wave solution(9).

(ii)Corresponding to the two family of periodic orbits tangent to the singular straight line l2:φ=1,defined by H(φ,y)=h,h ∈ (h2,h0)or h∈ (−∞,h2),Eq.(1)has two families of periodic wave solutions.

(iii)According to the theory of singular nonlinear waves,[2,18−21]corresponding to the two families of open orbits on the right side of the singular straight line l1:φ = −1,which are defined by H(φ,y)=h,h∈ (h1,h0)and pass through the point(φ0,0)with φ0∈ (−1,0),and left side of the singular straight line l1:φ=−1,which are defined by H(φ,y)=h,h ∈ (−∞,h1)and pass through the point(φ0,0)with φ0∈ (−∞,−1),Eq.(1)has two families of compactons.In addition,the family of orbits,which are tangent to the singular straight line l2:φ=1 and defined by H(φ,y)=h,h ∈ (h0,+∞),also give rise to a family of compactons.As illustration,we simulate these two families of compactons in Figs.3(a)and 3(b)by taking c=−2.

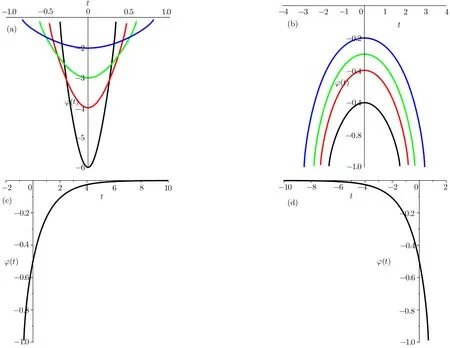
Fig.3 The families of compactons,kink-like wave solution and antikink-like wave solution to Eq.(1)when c=−2.(a)The family of compactions;(b)The family of compactions;(c)The kink-like wave solution;(d)the antikink-like wave solution.

(iv)According to the theory of singular nonlinear waves,[2,18−21]corresponding to the stable manifold and unstable manifold on the left side of the point E0(0,0),defined by H(φ,y)=h0,give rise to kink-like and antikinklike wave solutions.[18−20,23]Taking c= −2,we simulate the kink-like and antikink-like wave solutions in Figs.3(c)and 3(d). ?

Remark 1 We confirm that two types of orbits give rise to solitary wave solutions,that is,the homoclinic orbit passing the singular point in Fig.1(a),and the composed homoclinic orbit which is comprised of two heteroclinic orbits and tangent to the singular line at the singular point of associated system(5)in Fig.1(b).

Remark 2 We confirm that two types of orbits correspond to periodic wave solutions,that is,the periodic orbit surrounding a center in Fig.1(a),and the homoclinic orbit of associated system(5)which is tangent to the singular line at the singular point of associated system(5)in Fig.1(b).

4 Conclusions

In this paper,we show the existence and dynamics of several specific types of bounded traveling wave solutions.Additionally,we confirm abundant dynamical behaviors of the traveling wave solutions to the equation,such as two types of orbits correspond to solitary wave solutions,and two types of orbits give rise to periodic wave solutions.