用高斯光学和三级像差理论求变焦距物镜的初始解
2018-12-13史光辉
史光辉
(中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033)
1 引 言
一个好的变焦距物镜设计结果,不仅要求成像质量好,而且要求体积小、结构简单和工艺性能好。像ZEMAX和CODE.V那样的光学设计软件,虽然优化功能很强,但若想得到一个好的设计结果,初始解的选择仍然是至关重要的。求初始解的普遍做法是将已有的光学系统,或系统中的某个组元进行缩放。如果已有的光学系统和要设计的光学系统相仿,则不失为一种省事的方法。而有助于创新设计的、利用高斯光学和三级像差理论求初始解的方法却很少被应用。文献[1]认为,这种方法求解太繁琐,不如用现成的进行缩放的方法好。对于常规的光学系统,一般会有相仿的设计,但对于有特殊要求的光学系统,尤其是没有先例的、非常规的光学系统则很难有相仿的设计,如果硬要将一种不相干的光学系统或组元拿来缩放,则很难求得最佳的初始解。长期采用拿来进行缩放的方法,会使设计者对计算机过分依赖而不能很好发挥主观能动性。根据作者的经验,设计非常规光学系统时,若不是利用高斯光学和三级像差理论求初始解,则很难完成这些没有先例的光学系统的设计[2-5]。
20世纪60年代末,在薛鸣球院士的带领下,开始了利用高斯光学和三级像差理论求变焦距物镜初始解研究[6-7]。核心内容是用阻尼最小二乘法进行优化,求出各组元的、物在无限远的、规化的P、W。然后再用P、W求解各组元的结构形式。因此有人称它为P W法。此后有多篇文章介绍这一方法。但至今缺少一个有说服力的实例。
用高斯光学和三级像差理论求变焦距物镜初始解的一个理念是:对于大部分变焦距物镜光学系统来说,各组元都是由相贴合的透镜组成的,光线在其各组元半径上的高度和在主面上的高度差别不大,因此加厚了的光学系统,基本保留了原薄透镜系统像差,特别是高级像差特性,以及随着焦距连续改变而产生的像差变化特性。当然,随着相对孔径和视场的增加,透镜厚度也增加,像差的变化会逐渐加大。但一般情况下,仍然基本保留薄透镜像差特性。作者设计过10倍变焦距物镜和非常规形式的、23倍高倍率变焦物镜,最大相对孔径为F/1.6、最大视场58.7°,也都是用这种方法求初始解的。
另一个理念是:光学设计就是一个不断发现矛盾和解决矛盾,尤其是发现主要矛盾和解决主要矛盾的过程。这在用高斯光学和三级像差理论求初始解的过程中会得到充分的体现。因而利用光学设计软件进行像差优化,基本上只是起到使各种像差之间的矛盾达到最佳平衡的作用。
利用高斯光学和三级像差理论求初始解虽然繁琐、计算量大,但一旦编制好了程序,在计算机上进行计算就会变得容易和省时了。作者编制了3个这样的程序。
第一个程序[8]的功能包括解变焦方程,求出每个焦距下移动组元的移动量,以及各组元的间隔、倍率和每个组元的轴上光线和主光线出射角、光线高度。还给出凸轮曲线的公差。为了使连续变焦过程产生的像差变化量达到最小,以及能容易找出影响像差变化量和P、W及P0值的因素,程序没有采用阻尼最小二乘法,而是采用了解像差联立方程的方法。参与解方程的焦距位置可从最短焦距至最长焦距内任意选择。最后求解出各组元的、规化的、物在无限远的P、W和P0值,以及8个焦距位置的S1、S2、S3和S5值 。变焦距有各种形式,这可通过更换变焦方程来解决,其它部分是可以共用的。本文对这一程序又进行了较大的修改。
第二个程序[9]的功能是由规化的C1和物在无限远、规化的P、W求各组元的结构形式、光学材料和半径。每个组元的透镜组最少可由两个单透镜或一个双胶合透镜组成。最多可由任意排列的、多个双胶合透镜和多个单透镜组合而成。
第三个程序[10]是用于计算、选择和修正凸轮曲线的。 因为凸轮滚筒的大小以及曲线形式的选择会影响变焦距物镜的体积和重量,因此在求初始解时就应该考虑。这部分内容除了计算出每一步的两个移动量外,还计算出每一步的焦距、升角和倍率变化速度值。可以通过选择凸轮曲线的方法来减小凸轮的升角。如果需要,还可以兼顾变焦倍率变化的均匀性。如果不限制筒长和体积,甚至可得到曲率小、升角小和倍率变化均匀的解。
这样一来,用高斯光学和三级像差理论求初始解的过程中的所有计算,就可完全用计算机完成了。
下面通过一个10倍的、负组补偿的变焦距物镜设计实例来验证上述理念。本文说明,即使有现成的、可以拿来缩放的常规系统,用高斯光学和三级像差理论求初始解的方法仍有利于得出创新的、结构简单和小型化的初始解。变焦距物镜的参数为,焦距:10~100 mm 、F/4 、视场:3.44°~33.4°。(线视场直径为6 mm)。
2 用高斯光学求解变焦距物镜的高斯参数
2.1 求解变焦方程
通常的变焦方程应该称作是凸轮方程,即给出变倍组的移动量求出补偿组的移动量,若想得到确定的焦距,得经过多次逐次逼近计算,这对求初始解很不方便。因此需推导出在给定焦距后,求解两个移动量以及间隔等参数的变焦方程。

图1 两个移动组元的变焦距物镜 Fig.1 Zoom objective lens with two move components
如图1所示,上图的起始焦距F0位置,可选择任一焦距,一般选定为最长焦距或最短焦距。下图为任一焦距Fi位置。通常称f1为变倍组,f2为补偿组。当f1、f2以及f1的倍率和间隔确定后,从物点到像点的共轭距也就确定了。变焦方程首先要使任一焦距Fi位置的共轭距与F0位置相等。于是,
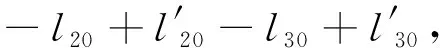
式中,l和l′表示物距和像距。用倍率表示则为:
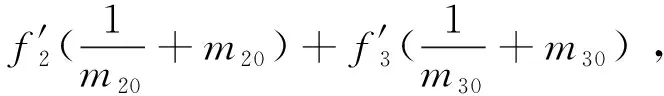
式中,m表示组元的倍率。要求出两个未知量X和Y,还需要一个方程:
(3)
解(2)和(3)两个方程后,得出二次方程:
(4)
其中:
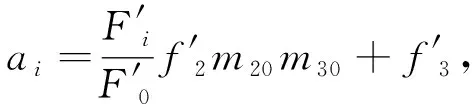
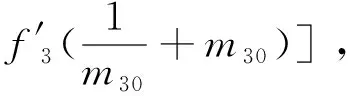
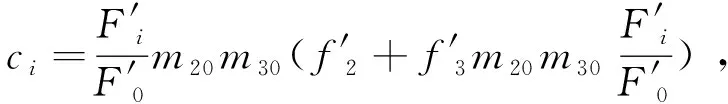
于是:
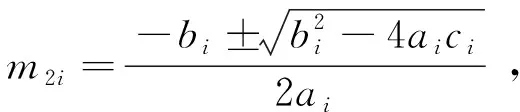
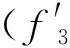
(9)
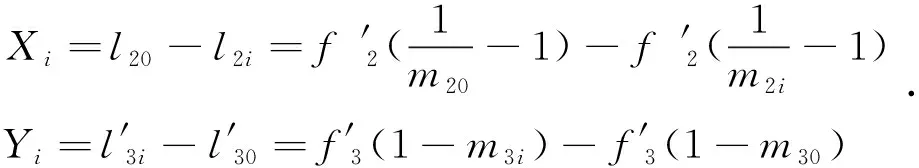
2.2 结构形式和各组元焦距以及组元间隔的选择
两个移动组中前面的一组称为前固定组,后面的一组称为后固定组,后固定组一般由分离的两组组成。这两组的形式一般有两种,一为正,正分离形式,一为正,负分离形式。前者会增加筒长;后者会使结构复杂以及会增加S4值。为了简化结构、不增加筒长和S4,本例后固定组的后组采用了由焦距相同和玻璃相同的正、负两个透镜组成的无光焦度形式。因为在此位置,它的主光线高度和角度比较小。5个组元的焦距依次分别为f1、f2、f3、f4和f5。 其中f4是为满足总焦距计算出来的。其它焦距是要进行选择的,选择的根据是有利于解决像差校正和结构的小型化的矛盾。为使各焦距的相对孔径相等,将光栏放在后固定组前组上。
首先要选择的是f1。它对筒长、体积、后面各组的相对孔径,主光线的偏角和S4都有很大影响,选择的主要依据是最长焦距的相对孔径大小。f2对筒长和S4影响很大。选取f2的主要依据是固定组和变倍组之间的间隔。这一间隔选取时要考虑的因素是筒长、主光线在前固定组上的高度和进入变倍组的入射角度。间隔大,筒长小,但主光线在前组的入射高度过高会增加前组口径,以及增加入射面到变倍组的主光线角度,从而增加轴外高级像差。因此,对于最短焦距的视场很大的、高倍率变焦物镜,这个距离应尽量小,视场超过60°时,为了降低入射到变倍组的主光线的角度,前固定组应采用负、正分离的复杂化形式。f3的选择范围很重要,其与补偿组和后固定组的偏角,以及补偿曲线的曲率、升角和公差都有关。无光焦度组单透镜的焦距选择原则是使该组的高级像差最小,有个最佳值。
变倍组和补偿组,补偿组和后固定组之间的间隔主要是以透镜组之间不相碰为主。有时也可通过调整间隔来小程度改变P、W和P0值。如本例的补偿组和变倍组间隔比较大就是为了减小前固定组和后固定组前组的P0值不得不采取的办法。后固定组两组之间的间隔的选择要看是否有利于减小无光焦度组的高级像差,其也有一个最佳值。
此外,在求初始解时,还要考虑拦光多少。可大致根据h和hp的值来确定拦光的多少。半口径等于h+hp时完全不拦光。本例设定最长焦距的边缘视场拦光不超过40%。要注意,主光线高度最大位置不是最短焦距,而是次短焦距,如本例在F=35处的主光学高度比F=10还大了3.5 m(表2)。忽略这一点,在视场很大的情况下,容易出现黑角。视场很大时,还要顾及光栏像差对拦光的影响。
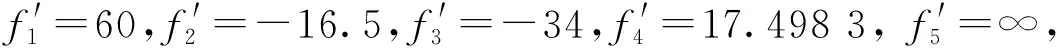

表1 两移动组件的移动量和各组之间间隔
2.3 倍率段选取
往下取的缺点是,因导程变短,变焦速度变快,因此速度变化更加不均匀了;此外,往下取还会增加补偿曲线的曲率和升角。相关数据见表2。
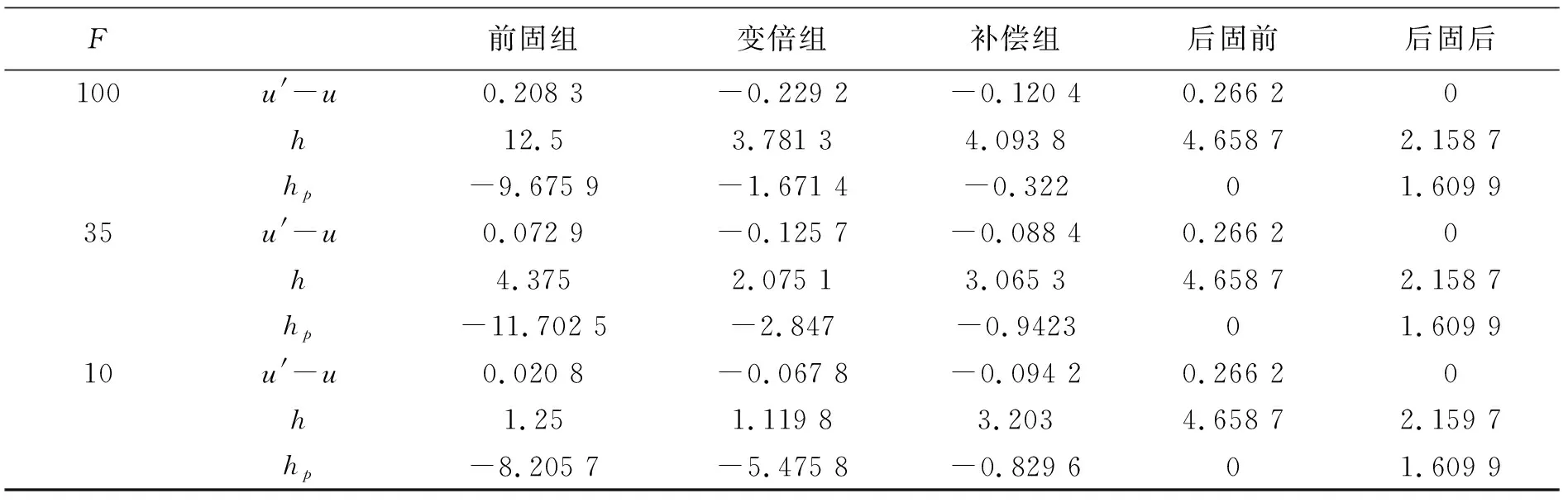
表2 F=100、F=35和F=10 各组元相关参数
2.4 双曲线凸轮
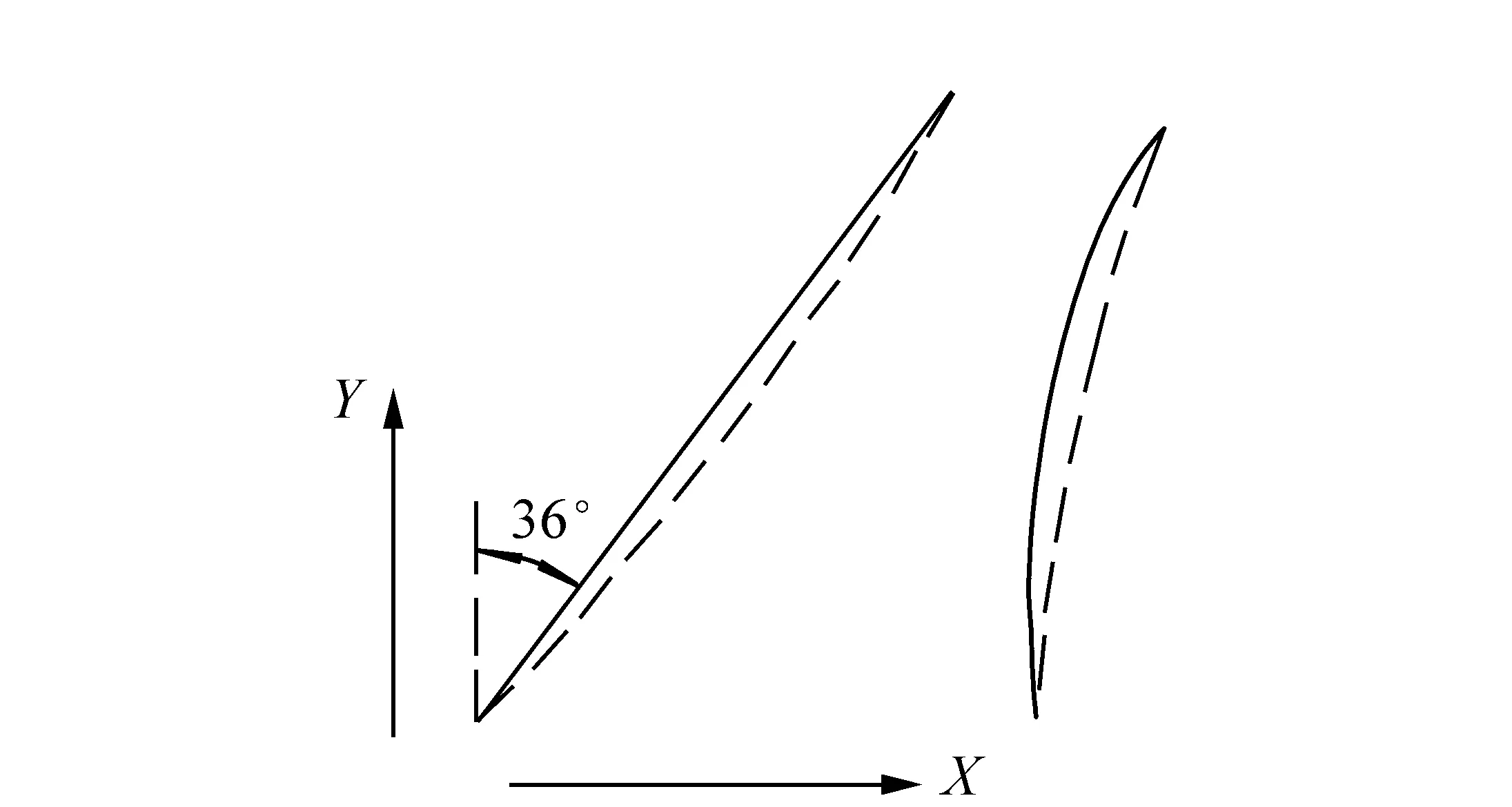
图2 凸轮曲线展开图。实线代表变倍曲线为直线,其升角36°。虚线代表变倍曲线为双曲线。X为焦距由10变化到100时,变倍组移动方向。Y为焦距由10变化到100的滚筒转动方向 Fig.2 Unfold curves of the cam. The solid lines express the variable curves in shape of strait line with rise angle of 36°. The dotted lines express the variable curves in shape of bi-curve. X:The moving direction of the zooming groups from F=10 to F=100. Y:The rotation direction of roller.
倍率选段往下取,导致补偿曲线的曲率和升角增加的同时,却减小了变倍曲线为直线时的升角。这样就可以采用双曲线凸轮来降低补偿曲线的最大升角。计算凸轮时,首先要确定凸轮总转角和滚筒直径。本例总转角设定为220°(应当尽可能往大取),滚筒直径为25 mm。得出变倍曲线为直线时的升角为36°,而补偿曲线的升角,从最短焦距的-4.2°升至最长焦距的58°(见图2实线)。按文献[10]的方法,通过选取不同曲线就可以降低凸轮的最大升角。最终得到变倍曲线的升角,从最长距的22.4°上升到最短焦距的43°,而补偿曲线的升角则由最短焦距的-5.3°上升为最长焦距的43°(见图2虚线),补偿曲线的最大升角降低了15°。这是通过让两条曲线的最大升角相同来达到凸轮曲线的最大升角最小化。如果还要降低最大升角,就要增大滚筒直径了。
3 用三级像差理论求各组元的初始结构
3.1 解像差联立方程组减小连续变焦过程中的像差变化量并求出每个组元的和P0值
无论什么形式的变焦距,也无论组元数多少,变量总是有限的,在用光学软件优化时也只能选几个焦距位置,因而也就这几个焦距位置的像差能得到校正。若保证在连续变焦过程中的成像质量,不能只考虑这几个焦距位置的像差校正,也要尽量减小其它焦距的像差。这是求初始解的重要内容之一。为了解决这一问题,过去采用阻尼最小二乘法求解各组元的两个变数。这一方法很难求出像差变化量小的解,也很难找出影响像差变化量的因素。其和用光学设计软件进行优化也没什么联系。因此作者改用解像差联立方程的方法,将参与解方程的焦距位置的像差校正到0,下面称这一位置为0点。通过0点焦距位置的选择,来减小除0点以外其它焦距位置的像差,下面称其为像差变化量。
(11)
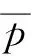
(12)
对于无光焦度组为,
(13)
此外还需要算出各组元的P0值:
(14)
方程中的w= -(i-i′)(i′-u),在文献[11]中该公式前边无负号。而在以上的方程中,和w有关项的符号都为负号。这是为了和已有程序接轨。
对无光焦度组,在S3和S5方程中的常数项为零。可以证明,方程中的φ在无光焦度组中,则为该组单透镜的值。系统每个参数的改变都会影响到像差变化量、同时也要影响到P、W和P0变化。因此要二者兼顾。
5个组元可有10个0点,分配给S1、S2和S3各3个,焦距位置都为F=100、F=55和F=10。剩下一个给最短焦距S5。S5不需要校正到0。对于大视场S5是有要求的,对于较小视场,可将它作为变数来参与求解。
由表3可见,除0点位置以外,其它焦距位置的像差都很小,S3几乎没变化。这是由于10个0点是比较充足的缘故。假如将只起校正像差作用而对高斯光学没有影响的无光焦度组去掉,则0点由10个减少到8个。因此需要去掉两个0点。除了把方程S5去掉外,再把F=55位置的S3方程去掉。得出的各焦距位置的像差见表4。显然,只因少了一个组元,像差S3的变化量就大多了,S1和S2也变大了。这说明,0点位置数,即系统的组元数对像差变化量影响很大,系统组元数越多,越有利于减小像差的变化量。

表3 解方程后得出的各焦距的像差系数

表4 去掉无光焦度组四组元的像差系数
为减小S3的变化量,可将两边的0点焦距向中间靠拢一点,结果变化量就变小了不少,见表5。这说明,通过改变0点的位置,可有效地减小像差变化量。如果使像差的正量和负量相等,就可使像差变化量达到最小。如果经过0点选择还达不到要求,就要选择改变其它参数,或用放大筒长的办法来解决了。解方程得到的结果,不仅要求像差变化量小,还要求P、W和P0值(绝对值)也小。二者往往是矛盾的。这要通过0点以及相关参数的选择来进行折中。

表5 采用0点方法时像差的减小量
由上述分析可知,为了得到好的成像质量且小型化,高倍率变焦物镜应采用多组元结构形式,低倍率的应采用组元少的形式。譬如对低倍率变焦距物镜,后固定组可以采用单组形式。但是,如果允许加大筒长,即便组元少的形式也可以设计成高倍率。因为后固定组只起到校正前边变倍分剩余像差的作用,而这剩余像差为S1、S2、S3和S5四个。因此多余两组元的后固定组对减小像差变化量不起作用。
3.2 由和求各组元的结构
各组元采用的结构主要根据最长焦距各组元的、轴上光线的偏角u′-u大小来确定。其次还要考虑主光线距离光栏的远近,以及主光线的偏角和高度。根据表2可知,前固定组、变倍组和后固定组前组的偏角都比较大,因此采用了双胶合加单透镜的形式。这有很多解,其中双胶合透镜,又分冕在前和火石在前,以及它们之间的光焦度分配。如果偏角很大,可以采用包括胶合透镜的,由4片以上的透镜组成的更复杂的形式,解就更多了。补偿组的偏角比较小,可采用双胶合或双分离形式。对于无光焦度组,可选择正透镜在前或负透镜在前。两块透镜的玻璃可选择折射率和阿贝数都相等,也可选择阿贝数相同,折射率不同的。因为这是一种正、负分离形式,所以无光焦度组可以满足很大的P、W和P0值的要求。但要将它放在合适的位置,本例中将它放在像面前边,离开光栏较远处。利用无光焦度这一特性,作者曾多次用到无光焦度组校正像差[5,12-13]。
P、W和P0值小的解容易得到高级像差小的解。P0值小,可选用的玻璃多,P0值大则需要采用较特殊的玻璃,如高折射率、高色散,高折射率、低色散,低折射率、低色散等。如果P0值小,P和W大,用普通玻璃也可能有解,但得出的半径小。
依据上述理念,得出各组元的结构。前固定组的P0值为-0.319 4,是比较大的,其中胶合透镜采用高折射率、高色散和低折射率、低色散玻璃ZF7和K9,而单透镜采用高折射率、低色散玻璃LAK2,取双胶合光焦度比为0.3,得到了高级像差小的解。前胶合透镜组的光焦度比小还有个好处是,透镜加厚后可以使主面向后移,这可以减小透镜加厚以后产生的像差变化量。如果将LAK2换成ZK9,则光焦度比为0.4才有解,解出的胶合面半径比用LAK2小。双胶合光焦度占比应尽量小,这会增大胶合面半径。对后固定组前组,因P0值比前固定组还大,为-0.446 6,因此用同样的玻璃,取光焦度比为0.4才有解。变倍组的P0值很小为-0.057 3,因此可选用玻璃比较多,允许的光焦度分配范围也比较宽,但P和W值比较大,经综合考虑后,选用ZF7和ZK9,双胶合占光焦度比为0.4。前固定组的双胶合选取火石在前,变倍组为冕在前。得出的胶合面半径都弯向光栏,可以有效地降低轴外视场的高级像差。对于补偿组,因偏角较小,且离光栏较近,主光线高度很低,不用考虑轴外高级像差,但因为P0值(-4.159 7)和P(-1.865 3)、W(1.802 6)都很大,从P0表可知[11],若采用双胶合形式,需两个折射率较低,且差值较小,以及阿贝数较小的玻璃才有解。即使有这样的玻璃,但得到的解要极度弯曲,致使半径很小,而且透镜加厚以后,还会令主面离开透镜组外比较远,这会使透镜组加厚后的像差产生大的变化。因此采用了双胶合分离的形式。这种正负分离的形式可满足很大的P、W和P0值。最终采用高折射率、高色散和高折射率、低色散玻璃ZF7和ZK9,且火石玻璃在前,解出的半径比较大,产生的高级像差小。有时还可以利用补偿组产生的正的高级像差来补偿前固定组产生的负的高级像差。对于无光焦度组,单透镜焦距可任意选择,可用来校正高级像差,最终选定为-22 mm。负焦距表示负透镜在前,用的都是ZK9玻璃。
究竟选哪一种结构形式和什么玻璃,最后要经过光线追迹算出像差后,由高级像差大小来确定。对无先例的、非常规光学系统要经过多次地选择和计算。对于像本例这样的常规光学系统,因为有了经验,追迹光线次数就少多了。得出的最终结果见表6。对于色差,令每组C1=0,因此C2=0。追迹光线计算像差是用国内程序CAOD程序完成的,其中色差的符号和ZEMAX程序相反。计算出的像差见表7。
表6 各组元的和p0值以及结构
表7中的像差系数和由解像差方程得出的像差系数(表3)不完全一致。这是由于在公式中采用了统一的、归一化的场曲系数μ值的缘故,而实际上各组元选用的玻璃不同,因而μ值也不同。但因μ值差别很小,对结果没什么影响。由非0点位置的F=70和F=30两栏的像差可见,像差变化量很小,和由解像差方程得出的结果是一致的。
由于C1=0,因此C线和F线在轴上交于一点,此点距d线轴上点的距离为0.086 mm(相当于1.14个波长)。这就是二级光谱的几何量。二级光谱是影响长焦距成像质量的主要因素。它随筒长的增加而减小,这和变焦距系统的形式,如正组补偿还是负组补偿,没多大关系。

表7 薄透镜系统像差
注:S2一列中的像差为O.S.C. C1一列中的色差是以波长为单位。
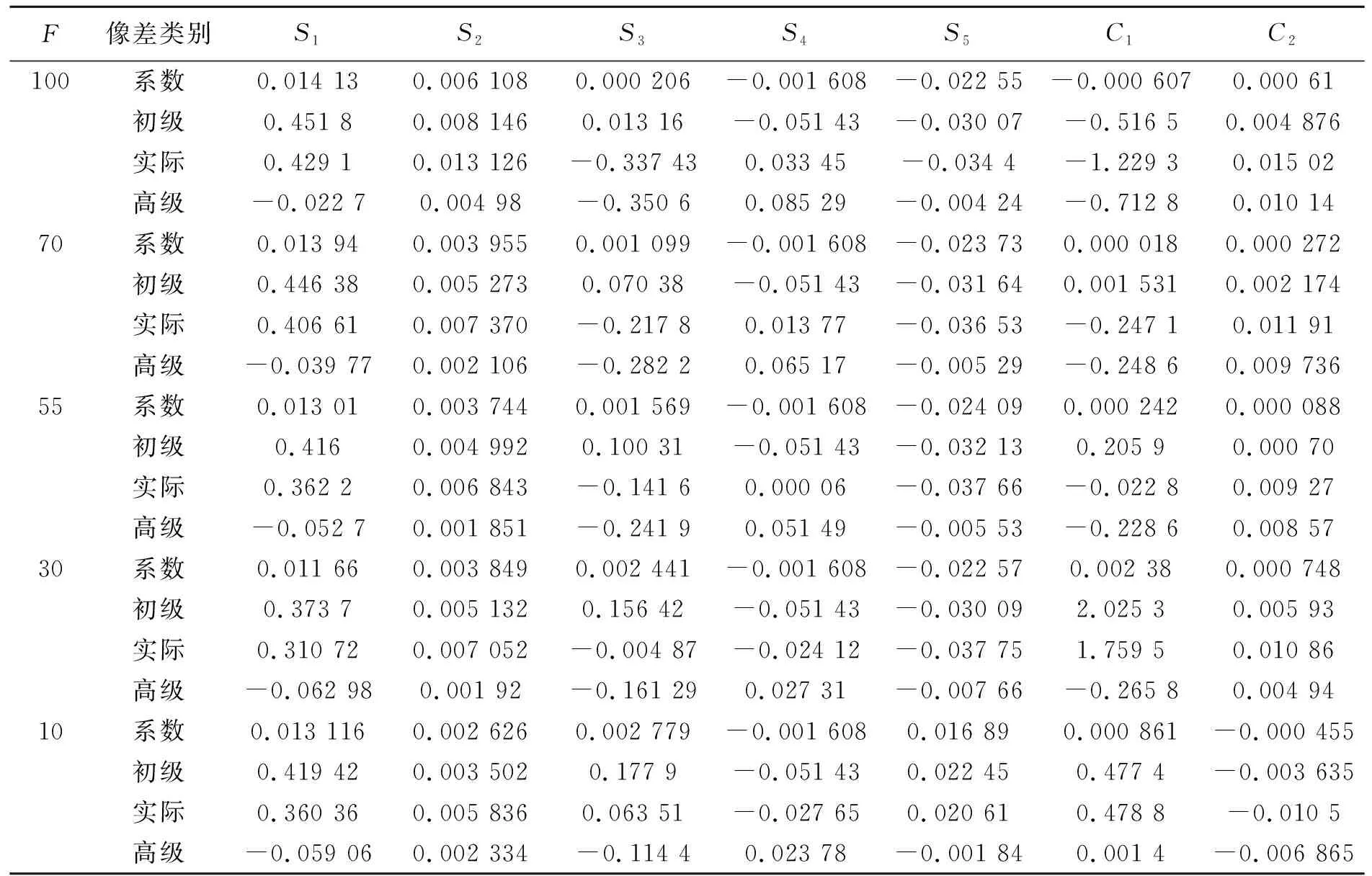
表8 初始解(厚透镜系统)的像差
经分析,透镜加厚后产生的色差和单色像差校正有矛盾。为只改变色差而单色像差保持不变,用折射率相等、阿贝数不等的玻璃ZBAF1换掉变倍组中单透镜的玻璃ZK9;用F2换掉无光焦度组中的ZK9。上述结果在ZEMAX软件上进行像差优化。经计算得到的像差见表8。和薄透镜系统比较,像差特别是高级像差变化不大。纵观各焦距的像差,最长焦距的O.S.C和像散的高级量大了点。但考虑到最长焦距的边缘光线要拦掉30%多,因此影响不会大。无光焦度组加厚以后,将产生像差很小的最后一面半径稍加修改,使之满足实际上的无光焦度,即满足u'-u= 0。因此焦距不再是无穷大。初始解结果见表9。

表9 初始解结构数据
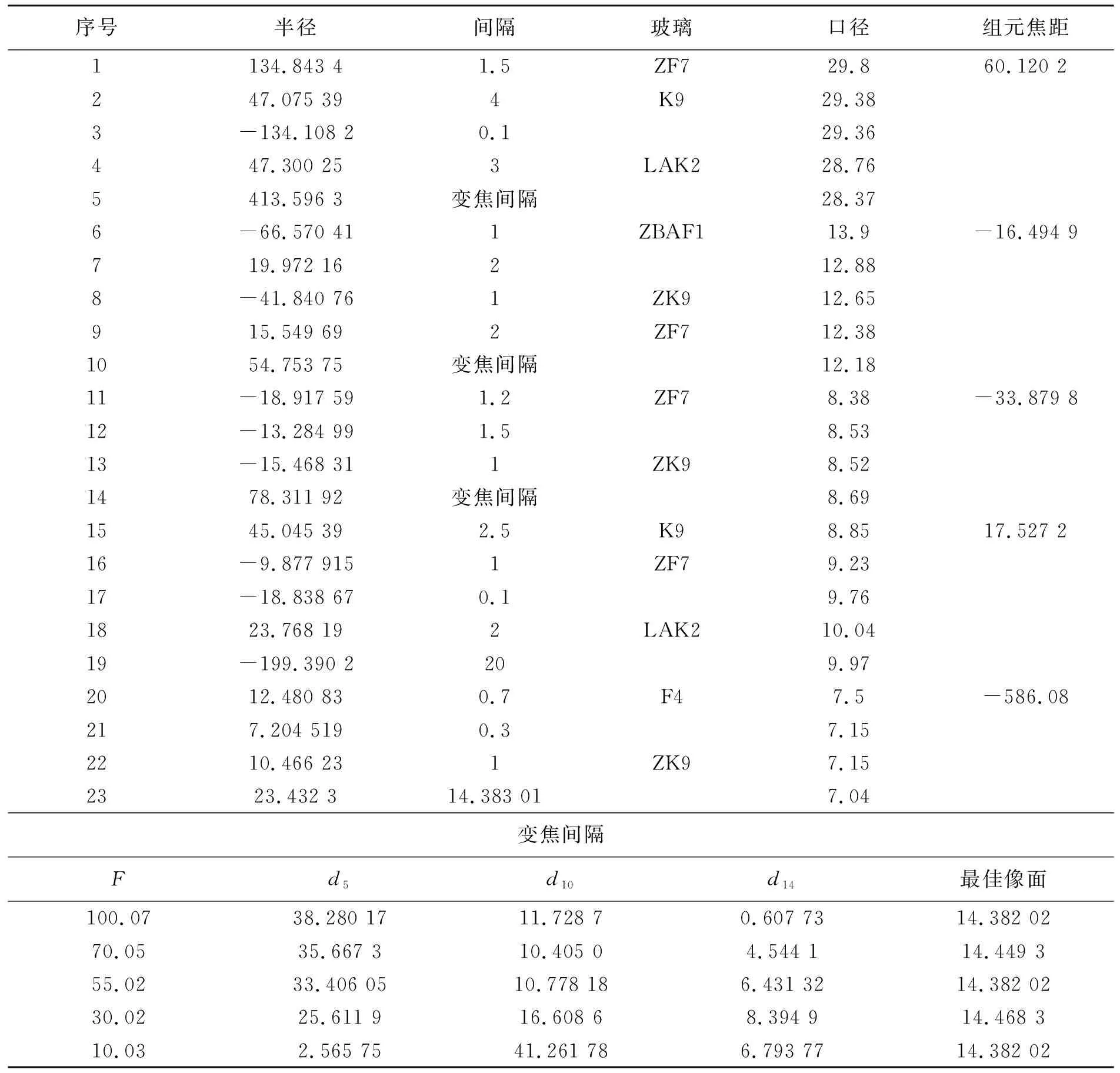
表10 最终设计结果结构数据
4 用ZEMAX 程序进行像差优化
用ZEMAX 或 CODE V 进行像差优化,在初始解合理的前提下,可以得到很好的效果[14-15],但如果优化结果中各组元的焦距和主面间隔与初始解相差较大,则前面求初始解的意义就要打折扣了。为此采用以下措施来尽量减小两者的差别。
首先按照0点理念,参与用ZEMAX优化的焦距位置应该是3个,且3个焦距位置应该和求初始解时的0点焦距相同,即F为100、55和10。这3个焦距位置都要在程序设定的默认操作数前边加进两个操作数,一是ISFN,以保证3个焦距的相对孔径和焦距值不变,二是ZTHI,以保证各焦距位置的总长度相等。结果是比较快地就得到了MTF值比较高的结果,但是各组元的焦距和主面之间的距离和初始解差别比较大。后来在最长焦距位置(也可以是其它焦距)上加进3个操作数,一是TOTR, 让光学筒长和初始解尽量保持相同。二是PETZ, 让匹兹瓦曲率半径(程序中有这个值)、也即S4 和初始解尽量保持相同 。三是PARB,将每一组元的、轴上光线的出射角(用Y方向的余弦表示)和初始解相同。最终取得了比较满意的结果。经优化得到的最终结果见表10。结构图和传递函数见图3。根据人眼的敏感程度,将D线C线和F线的权重比设为2∶ 1∶ 1.筒长为109.6 mm。
参与像差平衡的3个焦距F=100、55和10都处在最佳像面,而且都在一个像面上,而没参与像差平衡的F=70和30两个焦距的最佳像面偏离了参与像差平衡的3个焦距的最佳像面。见表10。两个焦距的最佳像面是用工具栏中的快速调焦得到的。为保证在连续变焦过程中的成像质量,应该按文献[10]的方法,对初始解得到的补偿曲线进行修正。其实,对一般的变焦距物镜设计,也都应当进行这一修正。
F=70.05和F=30.02的传递函数和参与优化的3个焦距相比差别不大,说明在连续变焦过程中,像差变化不大。这和初始解得到的结果一致的。
5 结 论
从设计过程可见,系统各参数,包括各组元的焦距、主面距离、结构形式、光学材料、光学筒长、凸轮形式、倍率段的选择,独有的后固定组形式的设计等,以及减小在连续变焦过程中的像差变化量等问题,在求初始解的过程中就已经解决了。从表10和表9的对比可见,透镜组弯曲状况也没有发生太大的变化。这说明了初始解所起到的作用是主导性的,而且能够给出一个好的初始解。而ZEMAX的优化功能只是起到像差最佳平衡的作用。但是,像差优化的工作量比求初始解大得多,没有ZEMAX这样先进的软件是很难得到好的设计结果的。两者还能用0点理念有效地连接起来。因此,利用高斯光学和三级像差理论求初始解,再用ZEMAX或CODE V进行像差优化是一个不错的选择。这一事实也表明,在具有先进的计算机技术和像ZEMAX和CODE V这样可以提供强大优化功能的光学软件的今天,传统的像差理论并没有过时,而是应该更加有用武之地。
