基于混沌映射与有限域GF(24)域乘法运算的电子病历图像的加密
2018-12-13刘西林严广乐
刘西林 严广乐
(上海理工大学管理学院 上海 200093)
0 引 言
随着互联网+技术的广泛应用和医院信息化的不断发展,电子病历已成为医院信息化进程中的必然结果,保证病历信息的真实性、完整性和对患者隐私信息的保护已成为当前电子病历中的热点问题[1]。随着健康信息技术的发展,医院之间可能就相关医患信息进行传递、交流,减少患者重复检验、检查及用药,提升医疗资源运用效率[2]。这在另一方面也增加了电子病历在操作、存储和传递方面的风险,使得电子病历越来越容易被盗取、复制、外泄、篡改。因此,对电子病历加密的研究具有重大意义。
由于图像具有冗余度高、数据量大、像素间相关性强等特点,传统的加密算法不太适用于图像加密,图像加密需要使用快速的方法[3]。为了提高数字图像的安全度,近年来对数字图像加密的研究很多[4],但有的存在密钥空间小的问题,有的存在信息熵偏差大的问题。电子病历图像作为携带病人信息的图像,目前对它的加密研究很少,而周广彬等[7]提出的混沌加密电子病历虽然达到了加密电子病历图像的效果,但是仅使用了Henon混沌算法进行加密。Henon作为简单的二维非线性混沌系统,有着低维混沌系统密钥空间小、安全性不高的缺点[8]。而且周广彬等对电子病历信息使用的是MD5算法产生的病历摘要,但是MD5算法已经被破解,从而使得安全性存在问题。
本文通过对电子病历图像使用SHA-1算法生成160 bit的哈希值作为病历摘要来监测电子病历传播的安全性;使用二维图像展成一维向量的无重复置乱和GF(24)域乘法的两次不同的扩散算法对电子病历图像进行加密,而后生成密文图像;三维Lorenz混沌映射产生密码。传输密文图像就达到了传播电子病历的目的,这样可以有效防止电子病历外泄,实现了对电子病历的隐秘传输[9]。这也使得不法分子看到的是密文图像,并不能看到真实的电子病历图,另一方面解密后的秘密图像再次经过SHA-1算法编码产生的病历摘要和发送方的病历摘要匹配,可以检查电子病历是否在传播过程中被私自篡改。这些方法使电子病历在传播中得到了多重保护。
1 SHA-1算法、混沌映射与GF(24)算法
1.1 SHA-1算法
SHA算法是密码散列函数家族,是经过FIPS所认证的安全散列算法。SHA-1算法就是其中一个,它可以将明文信息转换成字符串,再进行补位操作,然后附加长度通过函数计算得出唯一的160 bit的信息摘要[10]。图像的明文信息出现任何微小的变化经过SHA-1编译的哈希值即病历摘要都会发生显著的变化。每张电子病历经过使用SHA-1算法相当于拥有了“指纹”。
1.2 混沌Lorenz系统
本文采用的是Lorenz系统映射。其具体的动力学方程如下所示:

(1)
式中:a、b、c、w、r为混沌系统的参数,当a=10,b=8/3,c=28,-1.52≤r≤-0.06时,式(1)处于混沌状态[11]。
1.3 GF(24)算法
在密码学中,GF(p)即伽罗华域,是一个非常重要的有限域,并且域中必须有单元。GF(p)即modp,p为素数,结果是有限域中元素。在实际应用中,为了防止数据丢失,引入了GF(pw),其中p为素数,通常为2。伽罗华域的元素可以通过该域上的本原多项式生成,通过本原多项式得到的域,其加法单元是0,乘法单元是1。在GF(24)域中取既约多项式m(x)=x4+x+1。
2 加密与隐藏方案设计
方案设计流程图如图1所示。

图1 方案设计图
2.1 产生病历摘要
将电子病历图像转换成灰度图像,再经过SHA-1算法产生的哈希值作为病历摘要,值为42817e38ab192
e6b3bb2491578ab3cf65a5cf7ec。发送方保存该病历摘要,随后与接收方解密电子病历图像再经过SHA-1算法编码产生的哈希值进行匹配。
2.2 电子病历图像加密
本文提出的加密算法首先对原始图像的像素点的位置进行置乱操作;然后改变图像的灰度值进行正向扩散与逆向扩散;混沌Lorenz系统的参数和初始值作为密钥,产生对应的密码。解密过程是加密过程的逆过程。假设原始图像矩阵大小为M×N,具体加密步骤如下:
1) 给定密钥K的值即混沌Lorenz系统的各个变量的值(初值x0、y0以及z0和参数值w0)。迭代超混沌系统产生长度为M×N浮点数形式的伪随机序列。
2) 将明文图像矩阵按行展开成一维向量,记作A。借助于混沌系统产生的M×N的伪随机序列xi,i=1,2,…,M×N,X中重复出现的伪随机数只保留第一个,将{1,2,…,M×N}中没有X中的数值按从小到大的顺序添加到X的末尾,最后交换A(xi)与A(xMN-i+1)的位置,从而完成了二维图像展成一维向量的无重复置乱算法。
3) 置乱算法之后对像素点的灰度值采用GF(24)域乘法运算的扩散算法,本文采用的是正向扩散与逆向扩散相结合的方法。正向扩散和逆向扩散如下所示:
(2)
(3)
式中:P为明文展开成的一维向量,C、S为密码向量,初值C0、S1来自于密钥,i=1,2,…,MN。H表示数据的高4位,L表示数据的低4位。
经过一次置乱和正向与逆向两次不一样的扩散,从而得到了电子病历图像的密文图像。解密是加密的逆过程,不再赘述。
3 仿真实验
在MATLAB 7.1环境下对本文提出的算法进行仿真实验,得出结果。原始电子病历明文图像如图2所示,加密后电子病历密文图像如图3所示,正确密钥解密密文图像如图4所示,错误密钥解密密文图像如图5所示。

图2 电子病历明文图像图3 电子病历密文图像

图4 正确密钥解密密文图像 图5 错误密钥解密密文图像
接收方收到电子病历图像密文经过解密操作,再使用SHA-1算法编码产生的哈希值为:42817e38ab192
e6b3bb2491578ab3cf65a5cf7ec。若在传播中图像有改动再次编码得出的哈希值为:b3df52208a35ba5a0ada56
862a07a7a0b7f9d3bb(改动位置不同,哈希值不同)。
接收方将得到的哈希值与发送方的病历摘要进行匹配,若存在差异,说明该病历图像在传播中存在被篡改的行为;若相同,则说明病历图像安全传输。
4 安全性分析
4.1 直方图与x2检验分析
加密可以将明文图像转换成噪声从而隐藏信息。直方图与直方图的x2检验可以描述图像的相关性。一般情况下,图像像素灰度的直方图越服从均匀分布,x2检验值越小,越能有效地抵抗统计分析的攻击。电子病历图像明文直方图如图6所示,电子病历图像密文直方图如图7所示,电子病历图像明文与密文的x2值如表1所示。从图与表可知密文图像的像素灰度值更接近于均匀分布,说明加密效果比较好。
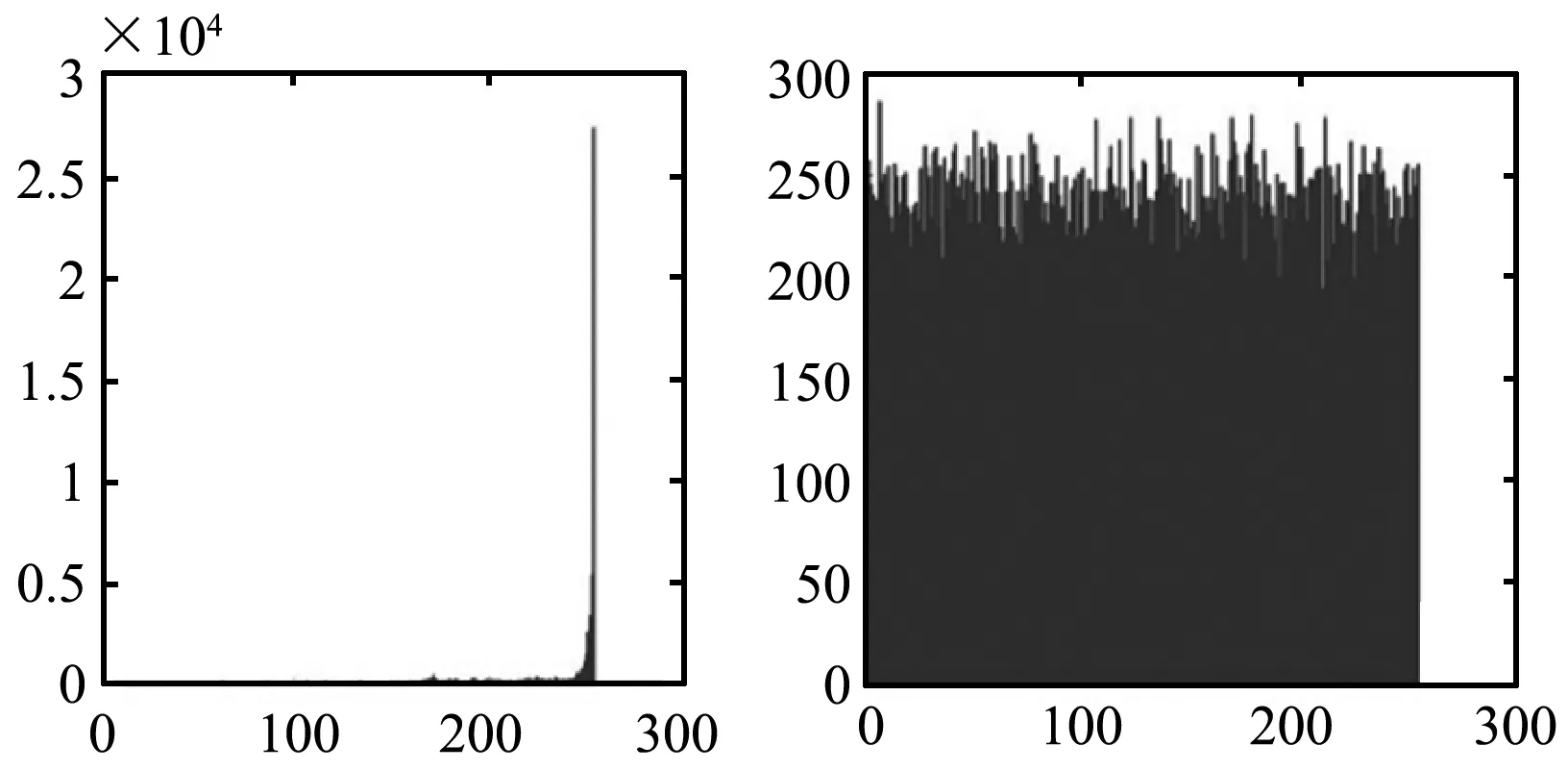
图6 明文直方图 图7 密文直方图

图像x2值明文3.244 2e+06密文267.321 9
4.2 相关性分析
明文图像相邻像素之间有很强的相关性,而这些相关性内部存在着明文的部分信息,若被不法分子发现利用,很可能会造成图像的泄露[12]。好的加密算法能够使得图像的像素之间的相关性变弱。本文从明文与密文图像中随机挑选了2 000对相邻像素点,绘画出相关性图像如图8所示,计算出了它们在水平、垂直、正对角与反对角的相关系数如表2所示。从图与表可以看出加密后图像像素之间的相关性明显降低,有效地保护了图像信息。相关系数的计算公式为:
(4)

式中:N为任取的相邻像素点的对数,它们的灰度值为(ui,vi),i=1,2,…,N,向量u={ui},向量v={vi}。

明文水平方向(a) 密文水平方向(b)

明文垂直方向(c) 密文垂直方向(d)

明文的正对角方向(e) 密文的正对角方向(f)

明文的反对角方向(g) 密文的反对角方向(h)图8 相关性图像

图像水平垂直正对角反对角明文0.274 10.775 50.117 90.142 5密文0.015 2-0.028 60.003 80.007 1
4.3 信息熵计算
信息熵反映的为图像信息的不确定性,一般认为,图像信息熵越大,信息量越大,事件的随机性越大[11]。为了体现本文算法的优越性,不仅计算出电子病历图像的明文与密文的信息熵,而且用本文算法加密经典图像Lena与其他文献进行对比,具体的结果如表3所示。信息熵的计算公式为:

(5)
式中:L为图像灰度等级数,P(i)表示灰度值i出现的概率。
对于L=256的灰度图像,信息熵H理论值为8,因为仿真实验得到电子病历的图像密文的信息熵几乎为8。又经过本文算法、文献[4]算法和文献[6]算法加密同一幅图像Lena计算信息熵,对比可以看出本算法的信息熵更接近8,表示本加密算法更能有效地抵抗数据攻击[13]。

表3 信息熵结果
4.4 密钥空间分析
密钥空间是指所有合法密钥的集合,加密算法越好,密钥空间越大[14]。本文的密钥为Lorenz系统的初始值,即K={x0,y0,z0,w0},其中x0∈(-40,40)、y0∈(-40,40)、z0∈(1,81)、w0∈(-250,250),x0、y0和z0的步长为10-13,w0的步长为10-12,可得密钥空间大约为2.56×1059,密钥空间约为197 bit,而文献[5]的密钥空间大小为(1016)2,因此,本算法的密钥空间更大,抵抗暴力攻击更有效。
4.5 密钥敏感性分析
密钥敏感性分析旨在将密钥做微小变化后,再加密同一图像得到的密文图像,若密文图像存在显著差别,则称密钥敏感性强,反之,密钥敏感性则弱[11]。衡量大小相同图像差别有几个常用指标:NPCR记录不同的像素点个数占全部像素点的比例,具体公式如下:
P2(i,j))|×100%
(6)

UACI记录两幅图像相应像素点的差值与最大差值(255)比值的平均值,具体公式如下:
(7)
BACI首先求得两幅图像的差图像的绝对值,然后将图像分解,计算全部小图像任意两个像素点的差值的绝对值的平均值与像素最大差值(255)的比值,具体公式如下(假设图像大小为M×N的P1和P2两幅图像):
(8)
式中:m为小图像块,i=1,2,…,(M-1)(N-1)。
本文从密钥空间中随机选取1 000个值,分别对x0、y0与z0改变10-13,w0改变10-12,计算的1 000个NPCR、UACI与BACI的平均值如表4所示。本文计算指标的结果很接近它们的理论期望值99.609 4%、33.463 5%与26.771 2%,说明密钥发生微小的变化后,密文相差很大,也进一步说明本加密算法密钥敏感性强,具有很强的抗差分能力。

表4 密钥敏感性分析结果 %
5 结 语
本文针对电子病历传输中的安全性问题提出了基于混沌映射与GF(24)域乘法运算的电子病历图像的加密算法。该算法通过对传输的电子病历图像进行加密与监测相结合的方法,增强了传输中电子病历图像的安全性与可靠性。实验结果表明,本算法密钥空间大,能有效抵抗暴力、统计以及差分攻击。该算法以后会有很强的潜在应用价值,但在提高加密与解密效率的问题上需要进一步提高,这个问题是今后需要研究的方向。
