基于CPD-SMOTE的类不平衡数据分类算法研究

彭如香 杨 涛 孔华锋 姜国庆 凡友荣

(公安部第三研究所 上海 201204) (信息网络安全公安部重点实验室 上海 201204)

0 引 言

类不平衡是指属于某一类别的观测样本的数量显著少于其他类别，通常情况下把多数类样本的比例为100∶1、1 000∶1，甚至是10 000∶1这种情况下为不平衡数据[1]。类不平衡现象普遍存在着不同应用领域中，如金融欺诈、网络入侵、垃圾邮件过滤、医学检测，直接采用传统的学习分类算法，分类准确率较低[1-3]。通常采用重采样方法处理类不平衡问题,重采样包括欠采用和过采样两种[1]。相比于传统欠采样方法，SMOTE算法克服传统随机欠采样导致的数据丢失问题。但是，SMOTE容易出现过泛化和高方差的问题，进而影响数据分布特征。为了解决这些问题，Borderline-SMOTE、ADASYN、LN-SMOTE等SMOTE改进算法相继被提出[4-6]。这些算法充分考虑小样本的分布，新增的样本不影响小样本的分布。然而这些算法未考虑小样本与大样本的交叉区域，最终形成的数据集将改变原有数据集的分布，而影响分类算法的准确性。

1 相关工作

1.1 SMOTE算法

SMOTE，即合成少数类过采样技术[1]。该算法由Chawla于2002年提出，是对随机过采样算法的一种改进。SMOTE算法的基本思想是对少数类样本进行分析和人工模拟，同时将模拟得到的新样本数据添加到原始数据集当中，使得数据正负样本比例均衡。

SMOTE算法流程如下：

(1) 对于少数类样本中每一个样本x，通过计算x到该类样本集所有样本的欧式距离，利用KNN算法，选出离样本x最近的k个同类样本点，得到其K近邻。

(2) 根据正负样本比例确定采样倍率为N，对每一个样本x分别随机从K近邻中选取N个样本，假设选择的近邻为x1,x2,…,xN。

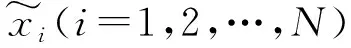
SMOTE算法的出现，改进了处理非平衡数据中传统的随机过采样算法，可以有效地对非平衡数据进行纠偏，整体上提高了模型的精度，同时还很大程度上降低了模型的误识率，这是SMOTE算法的优点[9]。其缺陷是无法解决非平衡数据的分布问题，容易产生分布边缘化问题，对于边缘的少类样本，对其进行K近邻生成样本也位于边缘且会越来越边缘化，这会使得正负样本的边界越来越模糊，加大样本分类的难度。

1.2 类不平衡算法评价指标

根据不同的应用场景，分类器考虑的评价指标也不同，通常基于混淆矩阵进行性能评价。混淆矩阵的定义如表1所示[7]：

表1 混淆矩阵定义

使用混淆矩阵可以得到如下几个评价指标：

精确度Accuracy=(TP+TN)/(TP+FN+FP+TN)

召回率R=TP/(TP+FN)

准确度P=TP/(TP+FP)

召回率和准确度通常会出现矛盾，这样需要综合考虑，最常见的方法就是F-Measure(又称为F-Score)。 F-Measure是Precision和Recall加权调和平均，其定义如下：

另外，可以通过ROC曲线评价一个分类器好坏。ROC曲线是基于样本的真实类别和预测概率来画的，具体来说，ROC曲线的x轴是伪阳性率(FP/(TN+FP))，y轴是真阳性率(TP/(TP+FN))；AUC(Area Under Curve)被定义为ROC曲线下的面积。简单地说，AUC值越大的分类器，正确率越高。

2 CPD-SMOTE类不平衡数据处理算法

通过上述介绍，SMOET算法充分考虑小样本的分布，新增的样本不影响小样本的分布。然而该算法未考虑小样本与大样本的交叉区域，最终形成的数据集将改变原有数据集的分布，而影响分类算法的准确性[5-6]。

本文提出一种改进型SMOET——CPD-SMOTE。CPD-SMOTE通过考虑训练集小样本Si的特征、位置及其周围样本分布，来确定Si的强相关邻居集SCNi。以SCNi作为SMOTE最近邻居集，产生新的小样本。这里强相关邻居集SCNi满足：

1)SCNi每个元素都为小样本特征向量；

2) 对于SCNi每个元素Ck，Ck与Si组成的超矩阵中不包含大样本特征向量。

其算法如下：

算法1强相关邻居集确定算法

输出：所有小样本的强相关邻居集{SCN1，SCN2,…,SCNs}。

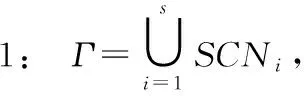
4: i=1;

5: For j in[2,s]

6: 判断zi与zj组成超矩阵中，是否包含Λ中的值；

7: 若不包含，则将zj加入到SCNi集合中；

8: Fori in[2,s-1]

9: For j in[1,i-1]

10: 判断SCNj中是否包含zi

11: 若包含，则将zi加入到SCNj集合中；

12: For j in[i+1,s]

13: 判断zi与zj组成超矩阵中，是否包含Λ中的值；

14: 若不包含，则将zj加入到SCNi集合中；

15: i=s;

16: For j in[1,s-1]

17: 判断SCNj中是否包含zi

18: 若包含，则将zi加入到SCNj集合中；

19: 若不包含，则将zj加入到SCNi集合中；

20: 计算非空强相关邻居集中元素数量平均值k;

21: 对于所有为空的强相关邻居集SCNi

22: 从大样本集Λ中随机挑选k个zi(小样本)的最近邻居Λ′

23: 对于Λ′中的所有uj

24: 取α为n维向量，元素取值为[0,0.5]之间的随机值；

25:znew=zi+(uj-zi)×α

26: 将znew加入到SCNi中

下面通过二维图简单说明强相关邻居节点选择方法，如图1所示。

图1 小样本x1的强相关邻居节点选择示意图

图1中，实心圆表示小样本节点，空心圆表示大样本节点。通过上述强相关邻居集确定算法，判断x2是否是x1的强相关节点的依据是由x2与x1组成的超矩阵中，是否包含大样本节点确定的。从图中看出x2满足该条件，故可将x2加入x1的强相关邻居集SCN1中。同理，x3也为SCN1的元素，而x4将不会被选到SCN1中。虽然x4到x1的距离小于x3,但是x4与x1之间存在大样本节点。若不考虑大样本节点的存在，采用传统的SMOTE,在x4与x1连线上随机产生新的节点，将影响大样本的分布，进而影响整个样本空间的分布。采用本文中的提出强相关邻居集确定算法，x4将不会被纳入到SCN1。然后，将SCN1作为SMOTE算法中邻居集产生新的小样本节点仍服从原来的分布。对于x5，根据上述判断条件，将不存在符合条件的邻居，所得到的强相关邻居集为空。考虑到这种情况，本算法充分考虑节点邻居数量均衡的特点，首先计算非空强相关邻居集中元素数量平均值k，然后从大样本集中随机挑选k个x5最近邻居，其次从x5与每个邻居的连线不超过一半(x5为起点)上随机挑选一个点作为x5的强相关邻居。至此，每个小样本的强相关邻居集都已确定。接下来将得到的强相关邻居集作为SMOTE算法中邻居集，完成新样本的生成，其算法过程如下：

算法2CPD-SMOTE算法

1: 设α为n维向量，元素取值为[0,1]之间的随机值；

2: 使用上述强相关邻居集确定算法，得出强相关邻居集{SCN1，SCN2,…,SCNs}

3: Fori从1到N

4: 随机挑选小样本Φ中的点zj：

5: 对于SCNi中元素zj

6:znew=zi+(zj-zi)×α

7: 将这些新的点加入S中

3 实验设置与分析

3.1 实验数据

本文实验采用来自Kaggle上的两个数据集，paySim和CreditCard Fraud Detection。

数据集paySim一种移动金融交易数据数据集，该数据集包括总样本数6 362 620个，其中正常交易样本数为6 354 407，欺诈交易样本数为8 237个，比例为772∶1。paySim数据集字段表如表2所示。

表2 字段含义表

数据集CreditCard Fraud Detection为信用卡交易数据。该数据集包含两天内发生的交易，其中284 807笔交易中有492笔被盗刷。数据集为不平衡数据集，类(被盗刷)占所有交易的0.172%。它只包含作为PCA转换结果的数字输入变量。该数据集属性除了时间和金额保留原始值，其他属性采用PCA转换进行了变换，转换特征V1，V2，…,V28，特征“Class”为响应变量，如果发生被盗刷，则取值1，否则为0。

通过上述分析，这两类数据均为不平衡数据集。

3.2 实验分析

paySim数据集和CreditCard Fraud Detection数据集都给出了目标列，为监督学习的应用场景。是否是欺诈交易或信用卡是否被盗刷是一个二元分类问题，本文选用基分类算法是支持向量机SVM算法作为基分类器[7-8]。

为了验证CPD-SMOTE算法与其他几种类不平衡处理算法SMOTE、Borderline-SMOTE、ADASYN、LN-SMOTE的性能，本文构建的分类算法模型首先分别通过这些算法将数据进行类平衡处理，使得数据正负样本比例均衡。然后分别采用SVM算法对数据分类，并采用10倍交叉验证方法验证模型的性能。这里SVM算法采用skik-learn算法集中，表3-表5分别给出了不同算法在两个数据集上评测指标均值，包括召回率R、F-Measure与AUC均值。实验结果表明，相比其他类平衡处理算法，CPD-SMOTE算法效果明显，学习性能更优。

表3 基分类器为SVM下的不同算法的召回率R均值

表4 基分类器为SVM下的不同算法的F-Measure均值

表5 基分类器为SVM下的不同算法的AUC均值

4 结 语

针对类不平衡情况对分类器的影响，本文在SMOTE算法的基础上，提出了CPD-SMOTE算法。该算法通过考虑训练集小样本的特征、位置及其周围样本分布，来确定小样本的强相关邻居集，以此作为SMOTE最近邻居集，产生新的小样本，实现数据正负样本比例均衡，并采用SVM算法对数据进行分类预测。在相同的基分类器SVM情况下，相比其他4种算法(SOMTE、Borderline-SMOTE、ADASYN、LN-SMOTE)，CPD-SMOTE算法在处理不平衡问题时能提升分类性能。