基于L1-L2联合范数约束的中药近红外光谱波长选择

任 真 李四海

(甘肃中医药大学信息工程学院 甘肃 兰州 730000)

0 引 言

中药具有物质成分多、作用机理复杂等特点，保证中药产品质量的可靠稳定是实现中药现代化必须要解决的关键问题。近红外光谱分析技术是20世纪90年代以后迅速发展起来的一种新型在线检测技术，具有简便、低成本、不破坏样品等优点，已在农业、食品、石油化工、药物质量控制等领域得到广泛应用。在中药质量控制方面，近红外光谱能够快速、准确地鉴别中药材的真伪、种类和产地，并且能够快速测定中药材中有效成分的含量以及中药辅料的品质[1-2]。

近红外光谱信号具有维度高、变量多重共线性严重等特点[3]。文献[4]用随机蛙跳算法(Random-frog)对生物柴油近红外光谱进行波长选择，分别建立了生物柴油含水量的偏最小二乘和支持向量机预测模型，取得了较好的效果。文献[5]建立了金银花醇沉过程中绿原酸含量的偏最小二乘回归模型，通过竞争自适应抽样CARS变量选择方法，提高了模型的预测精度。以上研究表明，基于波长变量选择的近红外光谱建模方法能够有效提高模型的预测能力。

现有的波长变量选择方法大多是封装式的：通过遍历搜索，找到变量空间的最优特征子集，使模型的均方根误差最小。由于特征子集的搜索采用前向、后向或蒙特卡洛随机搜索策略，对每一个特征子集的评价都需要重新训练模型，计算开销较大。嵌入式特征选择是机器学习中一类重要的特征选择方法，其通过最小化目标函数，使得特征选择和模型训练融为一体，同步完成，由于L1范数的稀疏特性，嵌入式特征选择能够自动实现变量选择，降低模型的过拟合风险，提高模型的可解释性。

本文通过在偏最小二乘回归模型中同时引入L1和L2正则项，建立一种嵌入式的光谱特征变量选择方法。将光谱变量选择和预测模型的建立融合在一起，解决光谱数据存在的多重共线性问题，提高了偏最小二乘回归模型的可解释性，实现了对当归中藁本内酯含量的快速、准确检测。

1 正则偏最小二乘回归算法设计

1.1 L1正则与稀疏性

正则化具有产生稀疏模型的能力[6-9]，Tibshirani[10]提出的线性回归Lasso模型通过将岭回归中的L2正则项替换为L1正则项，使模型具有变量选择和数据降维能力。

假设自变量矩阵X∈Rn×p，因变量Y∈Rn×1，线性回归的Lasso模型为：

(1)

式中：‖·‖2表示L2范数，β为回归系数向量，‖β‖1表示所有回归系数的绝对值之和，为L1范数罚，λ为惩罚系数。Lasso模型的解可通过坐标下降算法求得[11]：

对于i=1,2,…,p

1.2 偏最小二乘回归

偏最小二乘回归(PLSR)是主成分分析(PCA)和典型相关分析(CCA)的有效结合，其对CCA方法进行了进一步拓展。PLSR能有效解决高维变量之间的多重共线性问题，在近红外光谱的定量分析中得到了广泛应用[14]。

假设X和Y分别为光谱数据矩阵和待测含量矩阵，X∈Rn×p，Y∈Rn×q，X和Y的每一列均为零均值且标准差为1。

PLSR首先从X和Y中提取第一对主成分u1和t1，满足：Var(u1)→max，Var(t1)→max，Corr(u1,t1)→max。即u1和t1最大化且二者的相关性最大化。然后计算X和Y残差并根据残差继续提取下一个主成分。由于各投影方向之间相互正交，抽取的特征位于不同的投影方向，因此偏最小二乘能够有效去除变量之间的多元共线性。PLSR的最优主成分个数一般通过交叉验证方法确定。

1.3 正则偏最小二乘回归

近红外光谱数据具有高维度、小样本的特点。PLSR的投影向量是所有原始波长变量的线性组合，一方面，将部分噪声变量也纳入投影向量参与模型拟合会使有效变量的回归系数产生衰减，导致预测精度下降；另一方面，当p>>n，即p远大于n时，投影向量包含所有的原始波长变量导致模型可解释性不强。针对上述问题，在偏最小二乘回归模型中引入正则项，建立正则偏最小二乘回归RPLS算法，RPLS可形式化为如下的最优化问题：

(2)

s.t.αTα=1

式中：η、λ1和λ2均为常量，用于初始化算法，c为主成分载荷系数向量α的副本且与α取值相近。 式(2)可通过交替迭代算法求解[15]：

1) 固定c，求解α。对固定的c，式(2)变为：

(3)

s.t.αTα=1

令Z=XTY,η′=(1-η)/(1-2η)，则式(3)可重写为：

(4)

s.t.αTα=1

式中的α可通过拉格朗日乘子法求解。

2) 固定α，求解c。对固定的α，式(2)变为：

(5)

问题转化为因变量为ZTα的弹性网问题[16]，c可以通过LARS算法求解[17]。

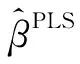
式中：Z1=XTY/‖XTY‖为第一投影方向单位向量。

Step2 当k≤K时

1.4 算法参数选择

对于单因变量回归问题，一般取η=1/2,λ2→∞。因此，算法的关键参数有两个：L1正则项系数λ1和最优主成分个数k。

λ1用于控制选择的波长变量个数，其值越大，选择的波长变量数越少，模型可解释性越好，但参与建模的变量数过少会导致模型预测能力下降。因此，λ1的选取要权衡稀疏度和模型预测能力，通过实验选择最优的λ1值。

最优主成分的个数k通过留一交叉验证法计算得到的Qk2值来确定[18]。

Qk2= 1-PRESSk/SS(k-1)

(6)

式中：PRESSk为使用前k个主成分对预留样本预测误差的平方和，SS(k-1)为使用前k-1个主成分对所有样本拟合误差的平方和。当Qk2≥0.097 5时，认为第k个主成分作用显著。

2 模型的建立

2.1 实验数据

采集甘肃不同产地的当归样本76个，使用美国Thermo公司的Nicolet-6700型近红外光谱仪扫描得到所有样本的近红外光谱，光谱范围为4 000 cm-1～10 000 cm-1，全谱共包括1 557个波数变量。76个当归样本的近红外光谱如图1所示。

图1 当归样本的近红外光谱

为消除基线漂移并提高光谱信号的信噪比，对原始光谱进行一阶导数结合正交信号校正预处理。当归中藁本内酯的含量采用高效液相色谱法(HPLC)测定[19]。

2.2 波长变量选择

将样本划分为训练集和测试集，训练集样本56个，测试集样本20个。使用训练集建立正则偏最小二乘回归模型对当归近红外光谱进行波长变量选择，因变量为当归中的藁本内酯含量。训练集和测试集中藁本内酯含量的分布情况见表1。

表1 训练集和测试集中藁本内酯含量分布

实验中用eta参数控制变量选择个数和模型稀疏度，对eta和k的最优组合采用网格寻优法确定。设定主成分k的搜索范围为[2,8]，步长为1，eta的搜索范围为[0.7,0.9]，步长为0.1。最优波长变量子集通过权衡训练集上的预测均方根误差和波长变量个数来最终确定。

3 实验结果与分析

3.1 波长变量选择结果

根据主成分数k和参数eta的搜索范围，共得到21个波长变量子集，分别建立以上变量子集在56个训练样本上的偏最小二乘回归模型。不同变量子集在测试集上的预测结果对比如图2所示。

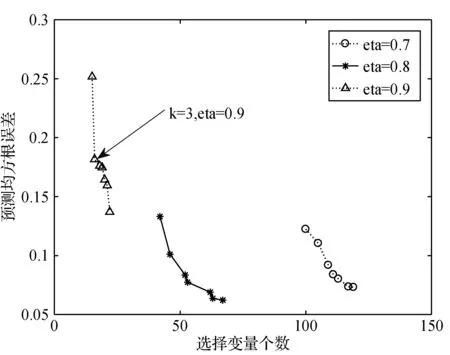
图2 k和eta对选择波长变量个数的影响

从图2可知，主成分个数k和eta对选择的波长变量个数都会产生影响，变量个数随着k的增加而增加，其中eta参数对变量个数的影响较大，eta值越大，选择的波长变量个数越少。当eta为0.7时，选择变量个数最少为100个，最多为119个，模型的拟合效果很好，但参与建模的变量过多，模型的可解释性不强。当eta为0.8时，选择变量个数最少为42个，最多为67个，此时选择的变量仍然过多。当eta为0.9时，选择变量个数最少为15个，最多为22个。综合考虑选择变量个数和模型的预测能力，本文选择eta=0.9,k=3为最优参数，此时共选择16个波长变量。分别为5 164.4 cm-1、5 218.4 cm-1、5 222.3 cm-1、5 226.1 cm-1、5 230.0 cm-1、5 233.9 cm-1、5 237.7 cm-1、5 241.6 cm-1、5 245.4 cm-1、5 249.3 cm-1、5 253.1 cm-1、5 257.0 cm-1、5 260.9 cm-1、5 704.4 cm-1、5 708.3 cm-1、 5 712.1 cm-1。根据近红外光谱的特征峰理论，所选择的波数大多位于C=O基团的伸缩振动吸收峰附近，与当归中的内酯类化合物有关，这说明所选择的波长变量具有较好的化学意义。

3.2 不同预测方法结果对比

使用RPLS选择的16个波长变量，在56个训练样本上建立偏最小二乘回归模型，取前3个主成分。对20个测试样本中的藁本内酯含量的预测结果见图3。

图3 藁本内酯预测值和实际值对比

从3可以看出，预测值和真实值之间非常接近，预测均方根误差RMSEP(root mean square error of prediction)为0.181 6，决定系数为0.995 7。RMSEP的计算公式如下：

(7)

为进一步说明本文波长变量选择方法的有效性，将RPLS与目前近红外光谱分析中常用的CARS、Random-frog等波长变量选择方法进行了对比分析。CARS算法迭代次数为1 200次，5折交叉验证，从1 200个子模型中选择交叉验证均方根误差最小的模型。Random-frog算法变量迭代次数为1 000次，实验中迭代达到200次时选择的变量结果基本稳定。根据三种方法所选择的变量，分别建立PLSR模型，表2对比了不同的波长变量选择方法的预测性能。

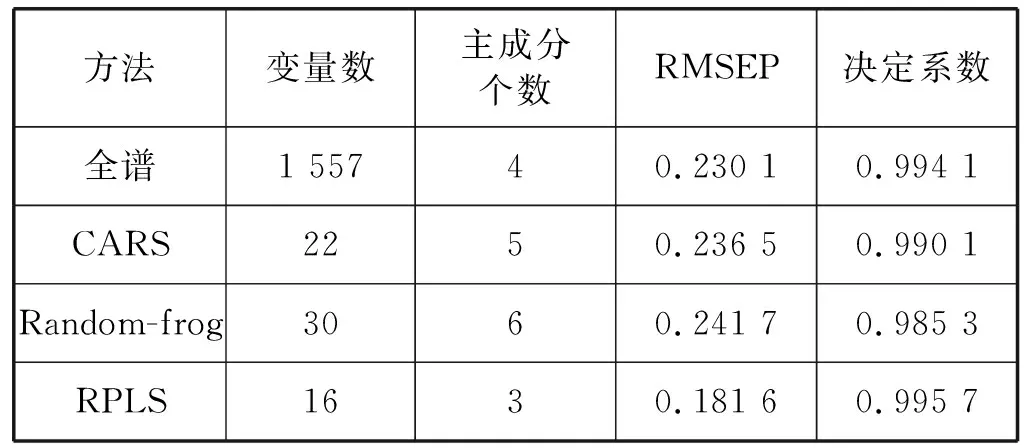
表2 不同变量选择方法的预测结果对比

从表2可以看出，与全谱建模相比，根据CARS和随机蛙跳选出的重要变量建模，能够获得与全谱建模相当的预测性能。但随机蛙跳需要预先设置种子变量，然后采用蒙特卡洛抽样技术，将其他波长变量依次添加到种子变量中形成不同的变量子集，根据均方根误差确定最优的波长变量子集，其迭代次数和变量选择结果均依赖于种子变量初始值，算法的计算开销较大。与CARS和随机蛙跳相比，RPLS波长变量选择方法通过设置eta和k的值来控制变量选择个数，并不是以变量子集的预测均方根误差来衡量变量子集的优劣，而是在变量稀疏性和预测能力之间取得折中，方法更为稳健。RPLS方法选择的波长变量数最少，预测性能优于CARS和随机蛙跳，且所选择的变量具有较好的化学意义，模型可解释性较好。

4 结 语

通过在偏最小二乘回归模型中引入L1和L2范数罚正则项，建立了正则偏最小二乘波长选择方法。该方法能够将近红外光谱中噪声变量在主成分上的载荷系数置为0，保留有效变量，达到选择重要变量的目的。与CARS和随机蛙跳变量选择方法相比，RPLS变量选择方法在选择的波长数、模型的预测精度及可解释性等方面均具有一定优势。

本文提出的正则偏最小二乘波长选择方法对噪声变量和有效变量施加相同的惩罚，对主成分载荷系数的估计是有偏估计。如何减弱甚至消除对有效变量的惩罚，得到载荷系数的近似无偏估计，提高近红外光谱波长变量选择的针对性将是下一步的研究方向。