考虑调整变化量和变步长的暂态稳定约束最优潮流模型
2018-12-12夏小琴
夏小琴, 徐 伟
(国电南瑞科技股份有限公司,江苏 南京 211106)
0 引言
随着特高压交直流互联、新能源接入及电力市场的发展,电力系统的运行方式越来越接近稳定极限,安全稳定问题日益突出。常规的最优潮流(optimal power flow,OPF)难以保证电网运行的动态安全性[1]。为了解决这一问题,暂态稳定约束最优潮流(transient stability constrained optimal power flow,TSCOPF)应运而生,受到了研究者们的广泛关注[2-16]。
与常规OPF相比,TSCOPF 的难点在于对微分转子运动方程的处理。目前主要有时域仿真法[2-8]、约束转换法[9-10]、轨迹灵敏度法[11-12]、能量函数法[13]等。时域仿真法将微分方程差分化为一系列的代数方程,其优点是原理清晰,可采用任意复杂的模型,但会导致计算规模庞大的问题。约束转换法中间计算量大,对模型敏感。轨迹灵敏度法在大扰动下准确性不高,甚至会影响计算收敛性。能量函数法的精确性同样比时域仿真法的精确性差。针对时域仿真法计算速度慢的问题,研究者们提出了减空间技术[5]、大步长数值方法[6-7]、并行计算技术[15]等有效手段。故障切除时刻网络参数发生突变,是暂态稳定分析的关键时间节点。若积分步长不能在整数步时到达故障切除时刻会影响TSCOPF计算结果的准确性。
大部分文献中的TSCOPF目标函数取系统网损最小[4,6-7]或发电燃料总费用最小[3,8,11-16],文献[5]同时取系统网损最小和发电燃料总费用最小。虽然以系统网损最小或发电燃料总费用最小的目标函数可以使系统方式调整到经济最优,但通常调整几乎全部的控制措施,调整量过大,无法满足电网事故后运行方式的快速调整需求。
基于此,本文提出一种新的暂态稳定约束最优潮流模型,取系统总调整变化量最小为目标,通过尽可能少的调整快速地将系统调整到安全稳定状态,并引入文献[16]的变步长策略,以故障切除时刻为时间节点微调两阶段的积分步长,实现对故障切除时刻和仿真结束时刻的精确取点。采用原始-对偶内点法对该模型进行求解。IEEE-9、NE-39及IEEE-118 3个测试系统的计算结果验证了所提方法的有效性。
1 目标函数选取
优化问题的数学模型可归纳如下:
minf(x)
s.t.h(x)=0

(1)
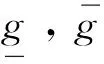
文献[3,8,11,13—14,16]的目标函数如式(2)所示;文献[4,6]的目标函数如式(3)所示;文献[5]分别考虑了如式(2)和式(4)所示的目标函数;文献[7]考虑了如式(5)所示的目标函数。
(2)
(3)
f(x)=∑(Pij+Pji)
(4)
(5)
式中:SG为发电机节点集合;SN为所有节点集合;PGi为发电机i的发电机有功功率;PDi为节点i的有功负荷;Pij(Pji)为节点i(j)节至节点j(i)的有功功率;ai,bi和ci分别为发电机i的费用系数。
以系统网损最小或发电燃料总费用最小的目标函数对原方式的调整量过大。本文取系统总调整变化量最小作为TSCOPF的目标函数,如式(6)所示。
(6)
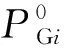
将式(6)转化为式(7):
(7)

(8)
2 两阶段步长微调策略
文献[16]采用二分法计算暂态稳定临界切除时间时,根据一定的步长更新策略使得刚好整数步时到达搜索区间的中点位置。本文引入该步长更新策略,分别微调故障中和故障切除后两阶段的积分步长,表达式如下:
(9)
式中:tc为故障切除时刻;Δt0为数值求解方法所需的积分步长,例如,目前公认隐式梯形法所需的积分步长为0.01 s;T为仿真结束时刻;符号「x⎤表示上取整,即取不小于x的最小整数。
3 TSCOPF模型
(10)
(10a)
(10b)

原始-对偶内点法具有计算速度快、收敛性好等优点,在电力系统中得到了很好的应用[3-7,17]。采用原始-对偶内点法求解上述模型,具体求解步骤参见文献[18]。
4 测试结果与讨论
本节以表1所示3个测试系统为例验证所提方法的有效性。目前只考虑单重故障。故障节点的故障类型为三相短路。计算程序在64位Matlab R2016b上实现,计算机配置为Intel(R) Core(TM) i7-2640M 2.8 GHz,4 GB内存。
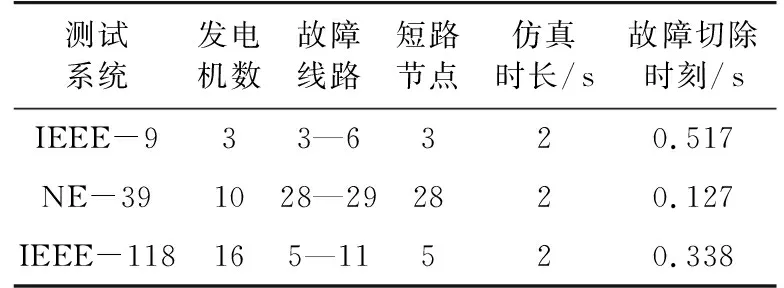
表1 测试系统概况Tab.1 Overview of the test systems
IEEE-9系统的两阶段步长取为0.009 942 s,0.009 953 s,NE-39系统两阶段步长取0.009 769 s,0.009 963 s,IEEE-118系统的两阶段步长取为0.009 941 s,0.009 952 s,实现了对故障切除时刻和仿真结束时刻的精确取点。
图1为各测试系统的互补间隙随迭代次数的变化曲线。从图1可以看出,各测试系统的对偶间隙单调收敛至零,算法具有良好的收敛性。

图1 互补间隙随迭代次数的变化曲线Fig.1 Variation curves of complementary gap with iteration times
各测试系统的调整后发电机转子摇摆曲线如图2所示。可见,所有发电机的转子相对角度均在-100°至100°范围内,满足了在仿真时间内各发电机不失稳的要求。

图2 调整后转子摇摆曲线Fig. Swing curves after adjustment
各测试系统在式(3)所示网损最小目标和本文目标下的调整量分别列于表2至表4。
可见,传统网损最小目标调整量在各故障切除时刻下相同,故障切除时刻较小时调整过大;本文目标调整量与系统失稳程度密切相关,避免了对原方式的过调。

表2 IEEE-9系统调整量比较Tab.2 Power adjustment comparison of IEEE-9 system
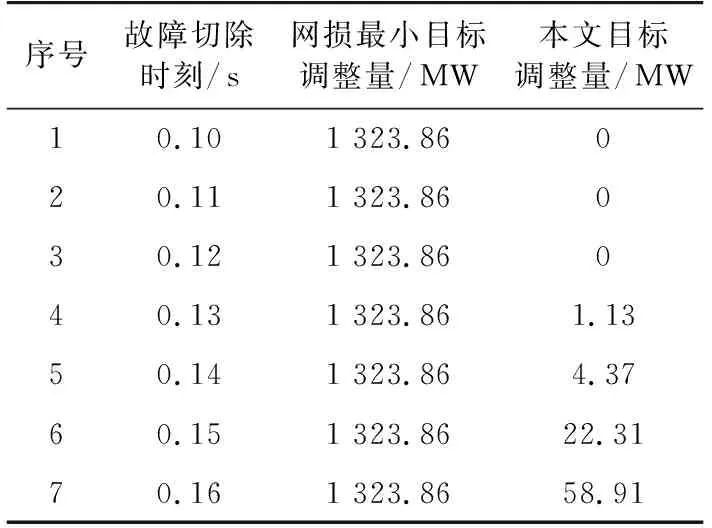
表3 NE-39系统调整量比较Tab.3 Power adjustment comparison of NE-39 system

表4 IEEE-118系统调整量比较Tab.4 Power adjustment comparison of IEEE-118 system
以NE-39系统0.15 s切除故障为例对上述两模型的有功功率网损及调整量进行比较。系统原有功功率网损为45.52 MW,传统网损最小目标和本文目标调整后的有功功率网损分别为31.56 MW和54.87 MW。传统网损最小目标减小了系统有功网损,本文目标的系统有功网损比原网损稍大。两模型下各发电机的调整信息如表5所示,传统网损最小目标下系统内可调发电机全部参与调整,而本文目标下只调整了图3所示的2台关键发电机。相比传统网损最小目标,本文目标虽然网损较大,但总发电机有功调整量和调整台数均明显减小,便于对系统进行快速的运行方式调整,利于电网事故后的快速恢复。

表5 NE-39系统发电机有功调整量Tab.5 Generator regulation of NE-39 system
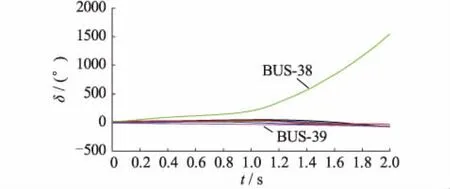
图3 NE-39系统初始转子摇摆曲线Fig.3 Original swing curves of NE-39 system
5 结语
本文提出了一种新的考虑调整变化量和变步长的TSCOPF模型。IEEE-9、NE-39及IEEE-118 3个测试系统的验证结果表明:(1) 两阶段变步长时域仿真实现了对故障切除时刻和仿真结束时刻的精确取值;(2) 以调整变化量最小为目标的TSCOPF模型得出的目标调整与系统失稳程度密切相关,对运行方式的修正量小于传统模型,便于对电网事故后运行方式进行快速调整,提高了TSCOPF的实用化水平。
